при каких значениях дробь не имеет смысла - страница 2
1) При каких значениях переменной х дробь х-2 --------------------------------- х(во 2 степени)+4х-21 не имеет смысла???
2)Найдите корни уравнения 5х(во 2 степени)-8=(х-4)*(3х-1)+8х. 3)Дано уравнение х(во 2 степени)+2х+с=0, где с---некоторое число, х---переменная. Найдите значение с, при котором один из корней уравнения равен 6
Решение: 1)дробь не будет иметь смысла в том случае если знаменатель будет равен нулю. значит приравниваем выражение стоящее в знаменателе к нулю и решаем получившееся уравнение
получаем корни уравнения х= -7 или х=3. следовательно при х= -7, и при х=3 дробь не имеет смысла
3)т.к один корень 6 то подставляем вместо х число 6 и решаем относительно с. получаем что с=481. Найдите значение выражения: .корень четвертой степени под корнем 7 минус корень из 33 умноженное на корень четвертой степени под корнем 7 плюс корень из 33. № 2. сократите дробь : a-b / а умноженное на b в степени 1/2 +a в 1/2 умноженное на b № 3. 3х-2 под корнем =4-x здесь получаются два корня 2 и 9, а как сделать проверку, кокой именно корень подходит? № 4. решите систему уравнений x-y=8;
корень из х - корень из y =2
Решение:1. ⁴√(7 -√33) · ⁴√(7 +√33) = ⁴√((7 -√33)· (7 +√33)) = ⁴√(49 - 33) = ⁴√16 = 2
2. (a - b) / (a√b +b√a) = [√a + √b)(√a - √b)] / [√ab · ( √a + √b)] =(√a - √b) / √ab
3. √(3x - 2) = 4 - x
ОДЗ: 3х - 2 ≥ 0 → x ≥ 2/3
4 - x ≥ 0 → x ≤ 4
Итак, ОДЗ: х∈ [2/3; 4]
3x - 2 = (4 - x)²
3x - 2 = x² -8x + 16
x² - 11x + 18 = 0
D = 11² - 4·18 = 121 - 72 = 49 → √D = 7
x₁ = 0.5·(11 - 7) = 2 ∈ ОДЗ
х₂ =0,5 · (11 + 7) = 9 ∉ ОДЗ
Ответ: х = 2
4. х - у = 8 → у = х - 8 подставим в нижнее уравнение
х - √у = 2 → х - √ (х - 8) = 2 решаем это уравнение при условии, что
ОДЗ: у≥0 и х - 8 ≥ 0, т.е. х ≥ 8
√(х - 8) = х - 2 и ещё х - 2 ≥ 0 → х ≥ 8
Итак, ОДЗ: у ≥ 0; х ≥ 8
х - 8 = (х - 2)²
х - 8 = х² - 4х + 4
х² - 5х + 12 =0
D = 5² - 4·12 = 25 - 48 = -23 (решений нет)
Ответ: решений нет1. Сократите дробь X-7 / корень из X-7
2. При каких значения переменной дроби X-7 / X+3, X-6 / X+24 равны?
3. Решите систему уравнений x-y=3
2x в квадрате + y в квадрате =9
4. Известно, что 2
5. Решите систему неравенст X>=3
X<=7
6. Найдите одиннадцатый член арифметической прогрессии, если
a1=17,d= -8
Решение: Желательно выполнить проверку: подставить в "х-у=3" значения уже полученных переменных (все сходится).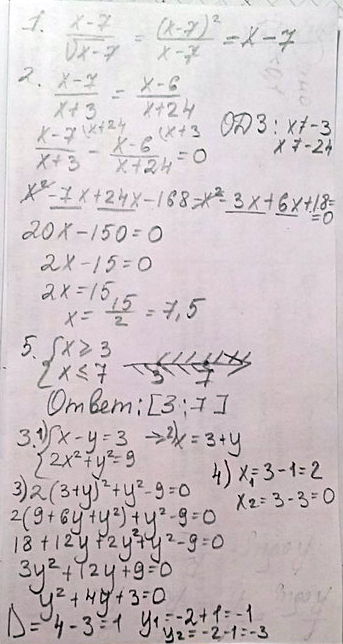
1) Бесконечная десятичная дробь устроена следующим образом. Перед десятичной запятой стоит нуль. После запятой подряд выписаны члены арифметической прогрессии An=dn + 2 (d - целое) Из полученной записи удалены минусы, если они есть. В результате получается рациональное число. Найдите это число.
2) Произведение всех делителей натурального числа N оканчивается на 333 нуля. На сколько нулей может оканчиваться число N?
3) Ученик должен был перемножить два трехзначных числа и разделить их произведение на пятизначное. Однако не заметил знака умножения и принял два записанных рядом числа за одно шестизначное. Поэтому полученное честное (натуральное) оказалось в три раза больше истинного. Найдите все три числа.
4) Первый набор чисел состоит из чисел 2, 4, 8, \( 2^{10} \). второй набор состоит из чисел 3, 9, 27, \( 3^{10} \). Числа разбили на пары. В каждой паре на первом месте число из первого набора, а на втором - какое-то число из второго набора. В каждой паре два числа умножили друг на друга и полученные произведения сложили. Найдите наименьшее возможное значение полученной суммы.
Решение: 1
Десятичная дробь является рациональным числом лите в том случае, когда она периодична. Арифметическая прогрессия не может быть периодической, она или монотонно возрастает, или монотонно убывает. Следовательно, при любом ненулевом значении d решения нет. Остается единственный случай, когда d равно 0. Тогда наше число принимает вид
х=0,2222222.
Умножим на 10
10х=2,22222.
10х-х=2
9х=2
х=2/9
1) При каких значениях y дробь равна 0
y^2-6y+9/y^2+3y
2) Пользуясь определением частного докажите тождество
m^2+3m-4/m-1=m+4
Решение: $$ 1)\frac{y^2-6y+9}{y^2+3y}=\frac{(y-3)^2}{y(y+3)}=0\to (y-3)^2=0,ye 0, ye -3\\y=3\\2)\frac{m^2+3m-4}{m-1}=m+4\\m^2+3m-4=0,m_1=1, m_2=-4\to m^2+3m-4=(m-1)(m+4)\\\frac{(m-1)(m+4)}{m-1}=m+4\\m+4=m+4\\3)\frac{a^4-7a^2+1}{a^2+3a+1}=a^2-3a+1\to \\a^4-7a^2+1=(a^2-3a+1)(a^2+3a+1)\\((a^2+1)-3a)((a^2+1)+3a)=(a^2+1)^2-(3a)^2=\\=a^4+2a^2+1-9a^2=a^4-7a^2+1\\a^4-7a^2+1=a^2-7a^2+1 $$
2 пример,2 способ.
$$ m^2+3m-4=(m-1)(m+4)\\(m-1)(m+4)=m^2+4m-m-4=m^2+3m-4\\m^2+3m-4=m^2+3m-4 $$$$ \cfrac {y^2-6y+9}{y^2+3y}=\cfrac {(y-3)^2}{y^2+3y} \\ \\\\ \cfrac {(y-3)^2}{y^2+3y}=0 \\\\\\ (y-3)^2=0 \\ y-3=0 \\ y=3 \\ y^2+3y=3^2+3\cdot 3=18 eq 0\\ Otvet:3 $$
частное - деление двух чисел
чтобы проверить, нужно частное умножить на делитель:
$$ \cfrac {m^2+3m-4}{m-1}=m+4 \\\\\\\ (m+4)(m-1)=m^2+4m-m+4=m^2+3m-4 - \ \ BEPHO

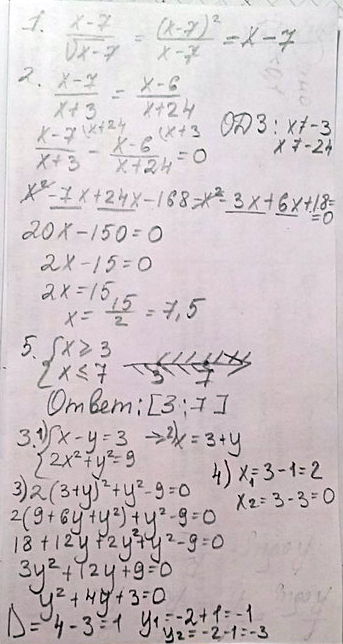
 Сложение и вычитание простых дробей
Для сложения и вычитания дробей с одинаковыми знаменателями нужно в первом случае сложить, а во втором вычесть их числители и результат сделать числителем новой дроби, а знаменатель подписать прежний.
Если знаменатели дробей различны, то нужно сначала привести все данные дроби к простейшему общему знаменателю.
При сложении или вычитании дробей с многочленными числителями и знаменателями в особенности важно...
Сложение и вычитание простых дробей
Для сложения и вычитания дробей с одинаковыми знаменателями нужно в первом случае сложить, а во втором вычесть их числители и результат сделать числителем новой дроби, а знаменатель подписать прежний.
Если знаменатели дробей различны, то нужно сначала привести все данные дроби к простейшему общему знаменателю.
При сложении или вычитании дробей с многочленными числителями и знаменателями в особенности важно...