при каких значениях дробь не имеет смысла - страница 3
Решить биквадратное уравнение:
1)x⁴-3x²-4=0(подробное решение)
2) При каком значении р в разложении на множители многочлена х²+рх-10 содержится множитель х-2?
3) Сумма квадратов двух последовательных натуральных чисел на 91 больше их произведения. Найдите эти числа.
Решение: $$ 1)\ x^4-3x^2-4=0 \\ t=x^2 \\ t^2-3t-4=0 \\ t_1=4 \\ t_2=-1 \\ x^2=4 \\ x=б2 \\ x^2=-1 $$Нет корней
Ответ: -2; 2
$$ 2)\ x^2+px-10=0 \\ 2^2+2p-10=0 \\ 2p-6=0 \\ p=3 $$
Ответ: 3
$$ 3)\ x^2+(x+1)^2=x(x+1)+91 \\ 2x^2+2x+1=x^2+x+91 \\ x^2+x-90=0 \\ D=1+4*90=361=19^2 \\ \\ x_1=\frac{-1+19}{2}=9\ \ \ \ \ \ \ \ \ x_2=\frac{-1-19}{2}=-10 $$
Ответ: 9 и 10 или -10 и -9
1) x^2 заменяем через букву (а)
получаем а^2-3a-4=0
находим дескреминант d=9-4*1*(-4)=25=5
находим корни х1=3+5 и разделить на 2=4
х2=3-5 и делить на 2=-1 брать нельзя это постороний корень !
ответ(5)
Решите уравнения а) x2 -четыре девятых(Это Дробь)= 0 б) модуль x=модуль x2 при каких значениях x верна запись Модуль x= -x?
Решение: x^2-4/9=0x^2=4/9
x1=-2/3
x2=2/3
IxI=Ix^2I
x=x^2
x=0;1
Модуль x= -x равна, когда х - отрицательное тлт х=0
а) $$ x^{2}-\frac{4}{9}=0 \\ x^{2}=\frac{4}{9} \\ x_{1}=\sqrt{\frac{4}{9}}=\frac{2}{3} $$
$$ x_{2}=-\sqrt{\frac{4}{9}}=-\frac{2}{3} $$
б) $$ IxI=Ix^{2}I \\ x=x^{2} \\ x_{1}=0 \\ x_{2}=1 $$
Модуль x=-x тогда, когда х имеет отрицательное значение
1. Используя определение модуля, запишите выражение без знака модуля:
|x-5|(x+3)
2. При каких значениях Х верно равенство:
|x^2-7x+12|=7x-x^2-12
3. Решите неравенство:
|x+4| строго меньше 2х
Решение: 1. Раскрываем модуль.
Если х-5>0, то
(х-5)*(х+3)
2 Раскрываем скобки
х^2+3х-5х-15
Упрощаем, получается
х^2-2х-15.
Это все был первый случай, когда выражение под модулем больше нуля, теперь раскроем модуль так, если выражение под ним отрицательное
1. Раскрываем модуль.
Если х-5<0, то
(-х+5)*(х+3)
2. Раскрываем скобки.
-х^2-3х+5х+15
Упрощаем, получается
-х^2+2х+15.
Все. Первое задание сделано.
Аналогично решаются остальные задания. Просто нужно помнить правило раскрытия модуля.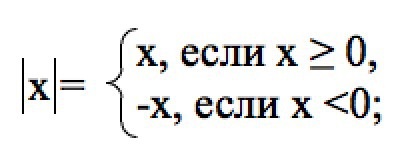
Найти все значения параметра k, при которых действительные корни m,n уравнения 4x²-2(k+8)x+k+17=0 удовлетворяют соотношению
(Ι-модуль)
|m+n|=|mn|+mn-0,25k-13\4
Решение: $$ |2(k+8)|=|k+17|+k+17-0,25k+\frac{13}4 $$
Корни выражений под модулем -8 и -17. Разобьём на 3 промежутка:
$$ 1.\;k\in[-8;\;+\infty):\\2k+8=k+17+k+17-0,25k-\frac{13}4\\2k-2k+0,25k=34-8-\frac{13}4\\0,25k=22,75\\k=91\\ 2.\;k\in[-17;\;-8):\\-2k-16=k+17+k+17-0,25k-\frac{13}4\\-2k-2k+0,25k=34+16-\frac{13}4\\-3,75k=46,75\\k=-\frac{187}{15}=12\frac{7}{15} \\3.\;k\in(-\infty;\;-17):\\-2k-16=-k-17+k+17-0,25k-\frac{13}4\\-2k+0,25k=16-\frac{13}4\\-1,75k=12,75\\k=-\frac{51}7=-7\frac27\\ $$
Найдите недопустимое значение для алгебраической дроби (а+1)(а+3)/2а(а-4)
Решение: недопустимое значение для дроби, когда знаменатель равен 0,
2а(а-4)≠0, т. е.
а≠0 или а≠4

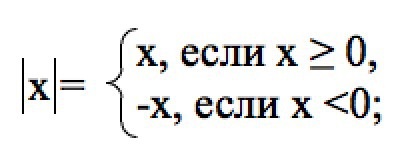
 Сложение и вычитание простых дробей
Для сложения и вычитания дробей с одинаковыми знаменателями нужно в первом случае сложить, а во втором вычесть их числители и результат сделать числителем новой дроби, а знаменатель подписать прежний.
Если знаменатели дробей различны, то нужно сначала привести все данные дроби к простейшему общему знаменателю.
При сложении или вычитании дробей с многочленными числителями и знаменателями в особенности важно...
Сложение и вычитание простых дробей
Для сложения и вычитания дробей с одинаковыми знаменателями нужно в первом случае сложить, а во втором вычесть их числители и результат сделать числителем новой дроби, а знаменатель подписать прежний.
Если знаменатели дробей различны, то нужно сначала привести все данные дроби к простейшему общему знаменателю.
При сложении или вычитании дробей с многочленными числителями и знаменателями в особенности важно...