дроби »
разложите на множители числитель и знаменатель дроби
5х^2+14х-3 (разложить на множители)
Решение: 5х²+14х-3 = 5х² +15х-х -3 = (5х²+15х)-(х+3) = 5х(х+3)-(х+3) = (х+3)(5х-1)
сначала 14 х разложили на слагаемые 14х = 15х -х
потом сгруппировали (5х² +15х) и (х+3)
потом из первой скобки вынесли за скобку общий множитель 5х
а потом еще раз вынесли общий множитель скобку (х+3)
в итоге получили два множителя (х+3) и (5х-1)Как разложить на множители квадратный трехчлен, если дискриминант равен нулю.
Решение: Находите дискриминант. ax^2+bx+c=0 допустим твое уравнение. значит дискриминант равен D=b^2-4ac. если дискриминант больше нуля,то получается два корня,которые находятся по формуле x1=(-b+корень из D)/2a или x2=(-b-корень из D)/2a. находите корни. разложенный на простые множители кв трехчлен = a(x-x1)(x-x2). все
если D=0,то один корень,находится по формуле -b/2a. тогда на простые множители раскладывается как a(x-корень уравнения)(x-корень уравнения). (тк этот корень уравнения считается за два)
если D меньше нуля,то корней нет и трехчлен не раскладывается на множители и просто оставляете такРазложите на множители квадратный трехчлен: 1) x^2 + x - 12; 2) 10y^2 - 9y + 2; 3) 6x^2 - 216; (через дискриминант)
Решение: 1) X^2 + X - 12 = ( X - 3 )* ( X + 4 )
D = 1^2 - 4*1*(-12) = 1 + 48 = 49 ; V D = 7
X1 = ( - 1 + 7 ) \ 2 = 6 \ 2 = 3
X2 = ( - 8 ) \ 2 = ( - 4)
2) 10Y^2 - 9Y + 2 = ( Y - 0.5 ) * ( Y - 0.4 )
D = 81 - 4*10*2 = 81 - 80 = 1 ; V D = 1
Y1 = ( 9 + 1 ) \ 20 = 10\20 = 0.5
Y2 = 8 \ 20 = 0.4
3) 6X^2 - 216 = 6 * ( X^2 - 36 ) = 6 * ( X - 6 ) * ( X + 6 )Найдите корни квадратного трехчлена и разложите их на множители и найдите дискриминант а) \( y2-6y+5 \) б) \( x2+14x+24 \) в) \( -y2+14y=33 \) г) \( -x2-10x-16 \) д) \( x2-8x-48 \) e) \( y2+16y+55 \) ж) \( x2-24x+144 \) з) \( -y2+18- 81 \)
Решение: Б) D=14*14-4*24=196-96=100
x1=(-14+10)/2=-2
x2=(-14-10)/2=-12
разложим на множители:
(х+2)(х+12)
в) -y2+14y-33=0
D=14*14-4*33=196-132=64
x1=(-14+8)/2=-3
x2=(-14-8)/2=-11
разложим на множители:
(х+3)(х+11)
Для разложения на множители используем формулу:
ax2+bx+c=a(x-x1)(x-x2) если коэффициент а равен 1, то перед скобкой ничего не надо, а в скобках пишете х минус твой корень. если корень с минусом, то в скобке будет плюс.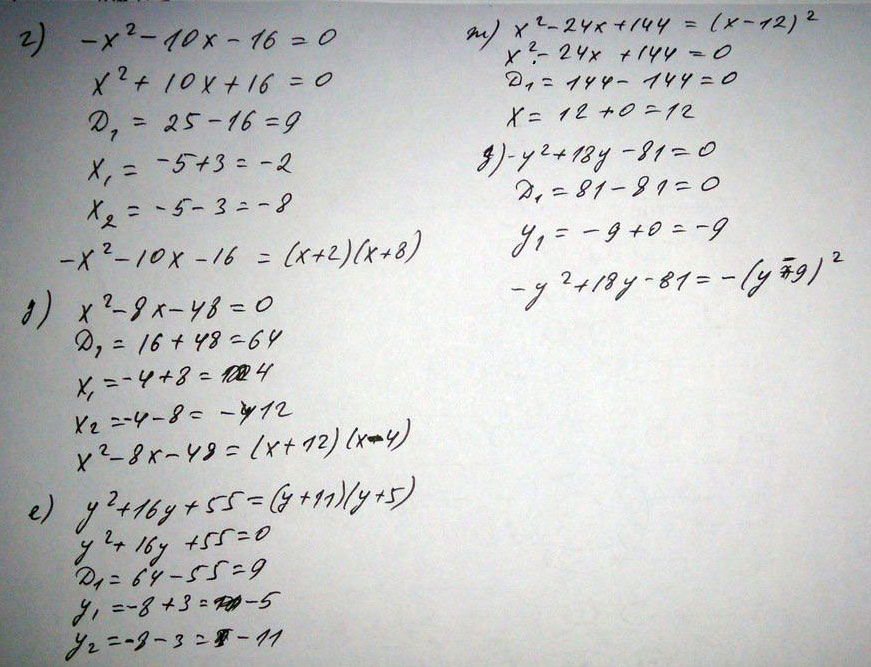
Разложите на множители трёхчлен: 16а^2+24а+9 Через дискриминат
Решение: 16a² + 24a + 9 = 0
D = b² - 4ac = 24² - 4 × 16 × 9 = 576 - 576 = 0 - имеет один корень.
x = - b / 2a
x = - 24 / 32 = - 0,75
Раскладываем по формуле : a ( x - x₁) ( x - x₂)
16 ( a + 0,75) ( a + 0,75)
или
= 16(a + 3/4)(a + 3/4) = (4a + 3)(4a + 3) = (4a + 3)^2 (в квадрате)

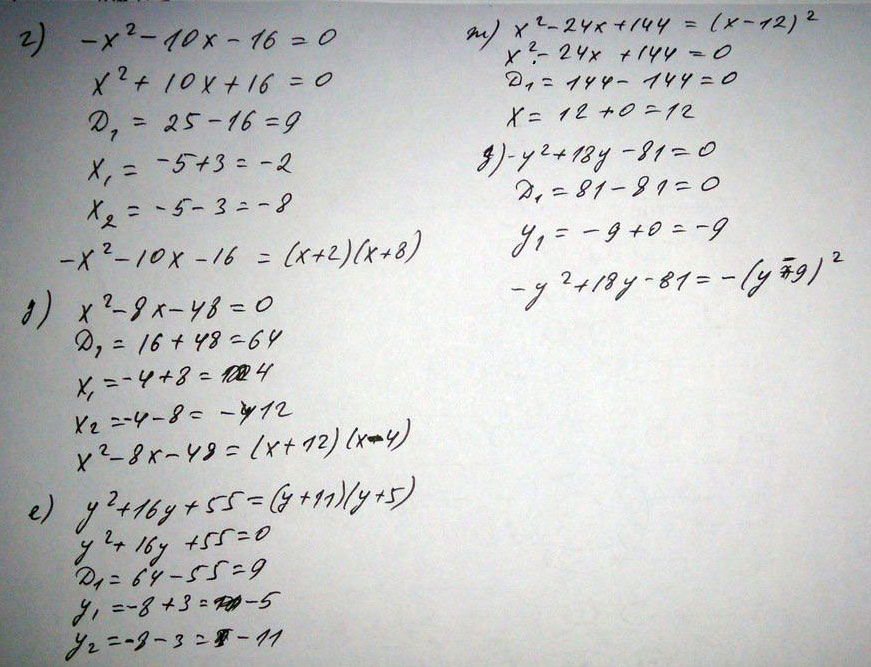
 Сложение и вычитание простых дробей
Для сложения и вычитания дробей с одинаковыми знаменателями нужно в первом случае сложить, а во втором вычесть их числители и результат сделать числителем новой дроби, а знаменатель подписать прежний.
Если знаменатели дробей различны, то нужно сначала привести все данные дроби к простейшему общему знаменателю.
При сложении или вычитании дробей с многочленными числителями и знаменателями в особенности важно...
Сложение и вычитание простых дробей
Для сложения и вычитания дробей с одинаковыми знаменателями нужно в первом случае сложить, а во втором вычесть их числители и результат сделать числителем новой дроби, а знаменатель подписать прежний.
Если знаменатели дробей различны, то нужно сначала привести все данные дроби к простейшему общему знаменателю.
При сложении или вычитании дробей с многочленными числителями и знаменателями в особенности важно...