дроби »
представить в виде дроби выражение - страница 2
1) решите уравнение: 5х квадрат -3х-2=0. 2) упростите: дробь вверху с квадрат внизу с квадрат - 4, - дробь вверху с внизу с-2. 3) Решите неравенство: 5(х+4)<2(4х-5). 4) а) построите график функции у=-2х+6,б)проходит ли график через точку А (-35;76)?.5) решите неравенство:х квадрат-1 < или равно 0. 6) представьте выражение дробь вверху а в пятой степени *а в -8 степени,внизу а в -2 степени,в виде степени и найдите его значение при а = 6
Решение: 1) 5x кв. -3х-2=0D (дискриминант) = -в кв. -4ac= (-3) кв. - 4*5*(-2)= 49>0 (2 корня)
х1= -в - v49 (корень из)/ 2a = - 0,4 - это первый корень уравнения.
х2 = -в + v49 (корень из) / 2a = 1 - второй корень.
3) 5х-8х < -10-20
-3х < -30
х=10
1) Представьте выражение a^-3 * (дробь) 1/a^-5 в виде степени и найдите его значение при a=0.1
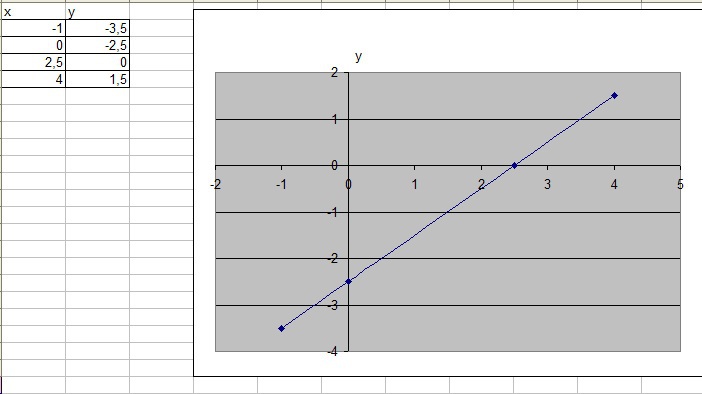
2) Постройте график функции y=x-2.5 и укажите координаты точек пересечения графика с осями координат.
Решение:1)
a^-3 * (дробь) 1/a^-5 = a^(-3)*a^5=a^2
при a=0.1 a^2=0,01
2) координаты точек пересечения с осью у (0;-2,5); с осью х (2,5;0)
Представьте выражение в виде дроби с целым рациональным знаменателем
\( \frac{1}{\sqrt[6]{y}- \sqrt{y}} \)
Решение: $$ \frac{1}{ \sqrt[6]{y}- \sqrt{y} } = \frac{ \sqrt[6]{y}+\sqrt{y} }{( \sqrt[6]{y}- \sqrt{y})( \sqrt[6]{y}+\sqrt{y})}= \frac{ \sqrt[6]{y}+\sqrt{y} }{( \sqrt[6]{y})^2- (\sqrt{y})^2}= \frac{ \sqrt[6]{y}+\sqrt{y} }{ \sqrt[3]{y}-y}= \\ \\ = \frac{( \sqrt[6]{y}+\sqrt{y})( \sqrt[3]{y})^2+y\cdot \sqrt[3]{y}+y^2) }{( \sqrt[3]{y}-y)( \sqrt[3]{y})^2+y\cdot \sqrt[3]{y}+y^2) }= \frac{( \sqrt[6]{y}+\sqrt{y})( \sqrt[3]{y})^2+y\cdot \sqrt[3]{y}+y^2) }{(\sqrt[3]{y})^3-y^3 }= \\ = \frac{( \sqrt[6]{y}+\sqrt{y})( \sqrt[3]{y})^2+y\cdot \sqrt[3]{y}+y^2) }{y-y^3 } $$
1. Представьте в виде обыкновенной дроби
А)0,2(5)
Б)0,(16)
2. Каким числам (рациональным или иррациональным) является значение числового выражения
А) (корень из 8 - 3)*(3+2корня из2)
Б) (корень из 2 - 1)^2 + (корень из 2 + 1)^2
3. b2=4 ; q=-1/2
Найти: S6
Решение: 1
A)x=0,2(5) 10x=2,(5)
y=2,5 10y=25,(5) 9y=25,5-2,5=23 y=23/9
x=23/90
0,2(5)=23/90
Б)x=0,(16) 100x=16,(16) 99x=16,(16)-0,(16)=16
x=16/99
0,(16)=16/99
2
А) (√ 8 - 3)*(3+2√2)=(√8-3)(3+√8)=(√8)²-3²=8-9=-1рациональным
Б) (√2 - 1)^2 + (√2 + 1)^2=2-2√2+1+2+2√2+1=6рациональным
3
b2=4 ; q=-1/2
b1=b2/q=4:(-1/2)=-4*2=-8
S6 =b1(q^6-1)/(q-1)=-8^(1/64-1):(-1/2-1)=-8*(-63/64*(-2/3)=-21/4=-5,25
1представьте -\( - \frac{x+2}{2-x} + \frac{4x}{x^2-4} - \frac{2-x}{x+2} \) в виде несократимой алгебраической дроби на одз
2 дано рациональное выражение
\( E(X)= \frac{5}{x^2+5} - \frac{4}{x^2+4} \)
а) найдите одз выражения E(X)
б найдите значение переменной X, при которых \( E(X) eq 0 \)
Решение: ОДЗ (знаменатили не равны 0)
$$ 2-x = 0; x^2-4 = 0; x+2 = 0 $$
$$ x = ^+_-2 $$
любое действительное за исключение 2 и -2, иначе
х є R\{-2;2}
$$ -\frac{x+2}{2-x}+\frac{4x}{x^2-4}-\frac{2-x}{x+2}=\\\\\frac{x+2}{x-2}+\frac{4x}{(x-2)(x+2)}+\frac{x-2}{x+2}=\\\\\frac{(x+2)^2+4x+(x-2)^2}{(x+2)(x-2)}=\\\\\frac{x^2+4x+4+4x+x^2-4x+4}{x^2-4}=\\\\\frac{2x^2+4x+8}{x^2-4} $$
2]
так как квадрат любого выражения неотрицателен, а сумма неотрицательного выражения и положительного положительно, то оба знаменаталя дробно-рационального выражения не равны 0 при любом действительном значении х(более того знаментали положительны при любом действительном значении х)
получается ОДЗ: вся действительная пряммая, иначе x є R? иначе
х є $$ (-\infty;+\infty) $$
(так как при лбом х: \(x^2+5>0; x^2+4>0\))
б)$$ E(x)=0; \\ \frac{5}{x^2+5}-\frac{4}{x^2+4}=0 \\ \frac{5}{x^2+5}=\frac{4}{x^2+4}=0 \\ 5(x^2+4)=4(x^2+5) \\ 5x^2+20=4x^2+20 \\ 5x^2=4x^2 \\ x^2=0 \\ x=0 $$
следовательно $$ E(x) = 0 $$ при $$ x = 0 $$


 Сложение и вычитание простых дробей
Для сложения и вычитания дробей с одинаковыми знаменателями нужно в первом случае сложить, а во втором вычесть их числители и результат сделать числителем новой дроби, а знаменатель подписать прежний.
Если знаменатели дробей различны, то нужно сначала привести все данные дроби к простейшему общему знаменателю.
При сложении или вычитании дробей с многочленными числителями и знаменателями в особенности важно...
Сложение и вычитание простых дробей
Для сложения и вычитания дробей с одинаковыми знаменателями нужно в первом случае сложить, а во втором вычесть их числители и результат сделать числителем новой дроби, а знаменатель подписать прежний.
Если знаменатели дробей различны, то нужно сначала привести все данные дроби к простейшему общему знаменателю.
При сложении или вычитании дробей с многочленными числителями и знаменателями в особенности важно...