представить в виде дроби выражение - страница 3
^ - значит степень.
I. разложите на множители:
1). u^2-9
2).4-a^2b^2
3). 1
- a^2-b^4
16
II. сократите дробь:
xz+yz 4a-a^2
а). б).
x^2-y^2 4a^2-64
III. представьте выражение в виде многочлена:
1) (2x-y)(y+2x)+x(4-3x)
2) (y-2)(y+2)+(3-y)(3+y)
3) (a+b)(a-b)-(a-b)^2
Решение: I. Pазложите на множители:1) $$ u^{2}-9=(u)^{2}-(3)^{2}=(u-3)(u+3) $$
2) $$ 4-a^{2}b^{2}=(2)^{2}-(ab)^{2}=(2-ab)(2+ab) $$
3) $$ \frac{1}{16}a^{2}-b^{4}=(\frac{1}{4}a)^{2}-(b^{2})^{2}=(\frac{1}{4}a-b^{2})(\frac{1}{4}a+b^{2}) $$
II. Cократите дробь:
a) $$ \frac{xz+yz}{x^{2}-y^{2}}=\frac{z(x+y)}{(x-y)(x+y)}=\frac{z}{x-y} $$
б) $$ \frac{4a-a^{2}}{4a^{2}-64}=\frac{-a^{2}+4a}{4(a^{2}-16)}=\frac{-a(a-4)}{4(a-4)(a+4)}=\frac{-a}{4(a+4)}=\frac{-a}{4a+16}=-\frac{a}{4a+16} $$
III. Представьте выражение в виде многочлена:
1) $$ (2x-y)(y+2x)+x(4-3x)=2xy+4x^{2}-y^{2}-2xy+4x-3x^{2}=\\=(4x^{2}-3x^{2})+(2xy-2xy)-y^{2}+4x=x^{2}-y^{2}+4x $$
2) $$ (y-2)(y+2)+(3-y)(3+y)=y^{2}-4+9-y^{2}=\\=(y^{2}-y^{2})+(9-4)=5 $$
3) $$ (a+b)(a-b)-(a-b)^{2}=a^{2}-b^{2}-(a^{2}-2ab+b^{2})=\\=a^{2}-b^{2}-a^{2}+2ab-b^{2}=(a^{2}-a^{2})+2ab+(-b^{2}-b^{2})=2ab-2b^{2} $$
1. Представьте в виде многочлена:
а) (3а+б) 2 квадрат
б) (y- 1/5 дробь x)(y+1/5 дробь x)
2. Преобразуйте в произведение:
а) m 2квадрат - 81 n 2 квадрат
б) 25+10p+p 2 квадрат
в) 6b 7 степени - 24b 4 степени
3. Вычислите, не используя калькулятор и таблицы:
( 17,6 2 квадрате - 2,4 2 квадрате): 10
4. Упростите выражение y (7x-y)+(x-y) 2 степени и найдите его значение при x =-1;y=1/5 дробь.
6. Докажите, что значение выражения (a-1)(f 2 квадрате+a+1)-a 3 кубе не зависит от значения а.
7. Решите уравнение.
(x+1)2 квадрате=36.
Решение: 1. Представьте в виде многочлена:
а) (3а+б) 2 квадрат=9a²+6ab+b²
б) (y- 1/5 дробь x)(y+1/5 дробь x)=y²-1/25*x²
2. Преобразуйте в произведение:
а) m 2квадрат - 81 n 2 квадрат=m²-81n²=(m-9n)(m+9n)
б) 25+10p+p 2 квадрат=(p+5)²
в) 6b 7 степени - 24b 4 степени=6b^7-24b^4=6b^4(b^3-4) можно разложить далее но там корни третьей степени будут
3. Вычислите, не используя калькулятор и таблицы:
( 17,6 2 квадрате - 2,4 2 квадрате): 10=(17.6²-2.4²)/10=(17.6-2.4)(17.6+2.4)/10=15.2*20/10=30.4
4. Упростите выражение y (7x-y)+(x-y) 2 степени и найдите его значение при x =-1;y=1/5 дробь.
y (7x-y)+(x-y) 2 степени =7xy-y²+x²-2xy+y²=x²+5xy (-1)²+5*(-1)*1/5=1-1=0
6. Докажите, что значение выражения (a-1)(f 2 квадрате+a+1)-a 3 кубе не зависит от значения а.
(a-1)(a²+a+1)-a³=a³-1-a³=-1 не зависит от а
a³-b³=(a-b)(a²+ab+b²)
7. Решите уравнение.
(x+1)2 квадрате=36.
!x+1!=6
x+1=6
x=5
x+1=-6
x=-7
-
x²2x+1=36
x²+2x-35=0
D=4+140=144
x12=(-2+-12)/2= -7 5
x=5
x=-7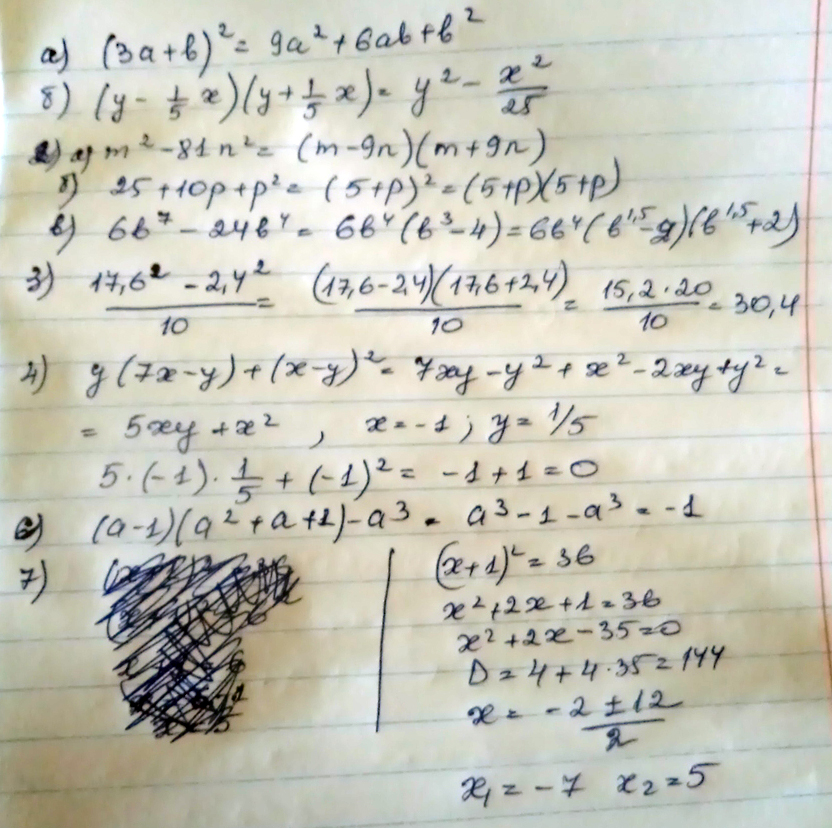
1. Вычислите:3^9*7^9/21^7
2. Представьте в виде многочлена:(1/3х-7у)^2
3. Решите уравнение:(5х-3)(2х+1)-(2х-3)(5х+4)=-3
4. Упростите выражение:4р/9р+9g-р/3р+3g
5. Решите неравенство:(2х-5)(2х+5)-(2х+3)^2 <_2
6. Разложите на множители: х^3-27у^3
7. Сократите дробь: х^2-bx-ax+аb/x^2-bx-ax-ab
8. В равнобедренном треугольнике АВС, АС-основание, ВD-высота этого треугольника, которая равна 5см. Периметр треугольника DBC равен 30 см. Найдите периметр треугольника АВС.
9. Упростите выражение:(-2/5а^4 b)^3*(-125а^3 b)
10. Пусть у/х=-3. Найдите значение выражения 3у^2-2ху+х^2/х^2+ху-у^2
11. Найдите точки пересечения параболы у=х^2 и прямой у=100.
12. Вычислите:0,4*0,8+0,4*1,2/0,6^2-0,4^2
13. Прямые m и n параллельные, с-секущая. Разность двух углов, образованных этими прямыми, равна 100 градусов. Найдите отношение большего из этих углов к меньшему.
14. Найдите углы треугольника, если они пропорциональны числам 4,5 и 9.
Решение: 1) 3⁹ * 7⁹ = (3*7)⁹ = 21⁹ = 21² =441
21⁷ 21⁷ 21⁷
2) (1/3x -7y)² = 1/9 x² - 14/3 xy + 49y² = 1/9 x² -4 ²/₃ xy +49y²
3) (5x-3)(2x+1)-(2x-3)(5x+4)=-3
10x²-6x+5x-3-(10x²-15x+8x-12)=-3
10x²-x-3-10x²+7x+12=-3
6x=-3-9
6x=-12
x=-2
Ответ: -2.
4) 4p - p = 4p - p = 4p - 3p = p
9p+9g 3p+3g 9(p+g) 3(p+g) 9(p+g) 9p+9g
5) (2x-5)(2x+5) - (2x+3)² ≤ 2
4x² -25 -(4x² +12x+9)≤2
4x²-25-4x²-12x-9≤2
-12x≤2+34
-12x≤36
x≥-3
6) x³-27y³=(x-3y)(x²+3xy+9y²)
8) BD=5 см
P(ΔDBC)=30 см
P(ΔDBC)=BD +BC+DC
30=5+(BC+DC)
BC+DC=25
В ΔABC AB=BC и AC=AD+AC=2DC
P(ΔABC)=AB+BC+AC=2BC+2DC=2(BC+DC)=2*25=50 (см)
Ответ: 50 см.
9) (-2/5 а⁴ b)³ * (-125 a³ b)= (-8/125 a¹² b³) * (-125 a³ b)= 8 a¹⁵ b⁴
10) y/x=-3
y=-3x
3y² -2xy+x² = 3 (-3x)² - 2x(-3x) +x² = 27x²+6x²+x² = 34x² = -34/11 =-3 ¹/₁₁
x²+xy-y² x² +x(-3x)-(-3x)² x² -3x² -9x² -11x²
11) y=x²
y=100
x²=100
x₁=10 (10; 100)
x₂=-10 (-10; 100)
12) 0,4 *0,8 + 0,4*1,2 = 0,4(0,8+1,2) = 0,4 * 2 = 2*2=4
0,6² - 0,4² (0,6-0,4)(0,6+0,4) 0,2 * 1
13) х - 1-ый угол
у - 2-ой угол
{x+y=180
{x-y=100
x=180-y
180-y-y=100
-2y=100-180
-2y=-80
y=40 - 2- ой угол
х=180-40=140 - 1-ый угол
140/40=3,5
Ответ: 3,5
14) х - коэффициент пропорциональности.
4х+5х+9х=180
18х=180
х=10
4*10=40 - 1-ый угол
5*10=50 - 2-ой угол
9*10=90 - 3-ий угол
Ответ: 40°; 50° и 90°.
№1
Представьте выражения (5а-2) в квадрате в виде многочлена.
№2
Выполните действия (-2х х в 4 степени у у в квадрате) в кубе
№3
Вычислите 8 в 16 степени умножить 8 в 10 степени разделить 8 в 24 степени.
№4Решите уравнение 2- 2х-5 разделить на 6(дробью)= 3-5х разделить на 4(дробью)
№5 Раскройте скобки и приведите подобные слагаемые 8(7-7у)-12(2у-5)+4(3у+7)
№6Решите уравнение (2х-1)(2х+1)-(2х+3) в квадрате=38
№7Вычислите ординату точки пересечения графиков функций у=5х-4 и у=х-12
Решение: 1
25a^2 + 4 - 20a
2
Не поняла, как выглядит выражение.
3
(8^16 * 8^10)/8^24 = 8^26/8^24 = 8^2 = 64
4
Домножаем на 12 обе части уравнения:
2(2 - 2x - 5) = 3(3 - 5x)
4 - 4x - 10 = 9 - 15x
11x = 15
x = 15/11
5
56 - 56y - 24y + 60 +12y + 28 = 68y + 144
6
4x^2 - 1 - 4x^2 - 9 + 12x = 38
12x = 48
x = 4
7
5x - 4 = x - 12
4x = -8
x = -2
y = -14
Ответ: -141) Приведите подобные слагаемые
15a -3b +5a +9b
2) Вычислите значение выражения
0,2 (2x -5)+1,2 (5x +3) при x =-4
3) Решите уравнение 5 -2 (3x -4)=4x-3
4) Представьте одночлен (3x в 6 )5 умножить 2x во второй, в стандартном виде
5) Упростите выражение 8a -(4a -5) во второй
6) Решите уравнение, записано виде дроби:4x -3 снизу 4, 5x +2 снизу 8 =3
7) Упростите выражение (с +d ) в квадрате
Решение: 1. Подобными слагаемыми будут 15а и 5а,3b и 9b. Можно записать так: (15а+5а)+(9b-3b).2. Для начала просто раскроем скобки и получится: 0,4х-1+6х+3,6= 6,4х+2,6
Затем подставляем значение х. 6,4*(-4)+2,6=-25,6+2,6=-23
3. Сначала раскроем скобки: 5-6х+8=4х-3
Затем всё что с х переносим влево, а что без х вправо:
-6х-4х=-3-8-5
-10х=-16
Умножаем всё на -1 и получаем10х=16,
отсюда х=16\10
х=1,6
5. Раскроем скобку по формуле: 8а-(16а^2+25-40а)
Затем избавимся от скобок и получим: 8а-16а^2-25+40а=-16а^2+48а-25
7. это формула: с^2+d^2+2cd

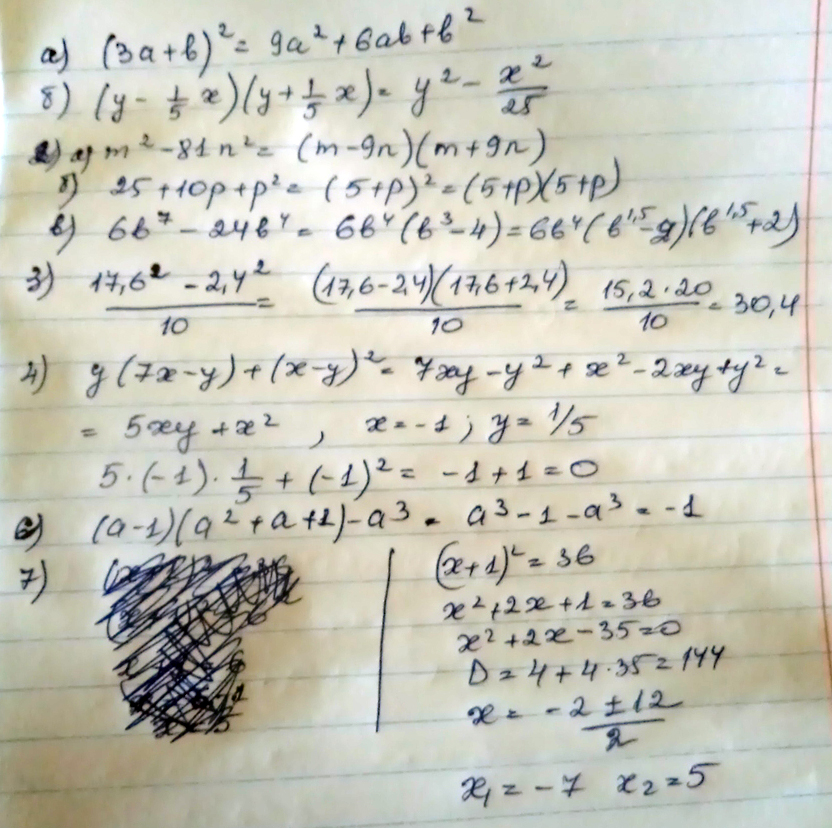
 Сложение и вычитание простых дробей
Для сложения и вычитания дробей с одинаковыми знаменателями нужно в первом случае сложить, а во втором вычесть их числители и результат сделать числителем новой дроби, а знаменатель подписать прежний.
Если знаменатели дробей различны, то нужно сначала привести все данные дроби к простейшему общему знаменателю.
При сложении или вычитании дробей с многочленными числителями и знаменателями в особенности важно...
Сложение и вычитание простых дробей
Для сложения и вычитания дробей с одинаковыми знаменателями нужно в первом случае сложить, а во втором вычесть их числители и результат сделать числителем новой дроби, а знаменатель подписать прежний.
Если знаменатели дробей различны, то нужно сначала привести все данные дроби к простейшему общему знаменателю.
При сложении или вычитании дробей с многочленными числителями и знаменателями в особенности важно...