дроби »

перевести дробь в обыкновенную - страница 5

  • перевести дробь в обыкновенную
    1) 0.(65) =
    2) -3.1(13)=
    3) 4.12(6)=
    4) 0.14(34)=
    5) 2.(123)=
    6) 1.2(8)=


    Решение: 1) 0,65(65) = 0,66 = \( \frac{66}{100} =  \frac{33}{50} \)
    2) -3,1(13) = -3,10 = -3 \(\frac{10}{100} = -3 \frac{1}{10} \)
    3) 4,12(6) = 4,13 = 4 \(\frac{13}{100} = 4 \frac{66}{100}\) 
    4) 0,14(34) = 0,14 = \( \frac{14}{100} = \frac{7}{50}\) 
    5) 2,123(123) = 2,123 = 2\(\frac{123}{1000} \)
    6) 1,2(8) = 1,30 = 1\( \frac{30}{100} = 1 \frac{3}{10} \)

  • Правило умножения и деления обыкновенных дробей, и как сокращать обыкновенные дроби. и еще как десетячную дробь перевести в обыкновенную и обратною


    Решение: Правило умножения дробей - числитель умножаем на числитель, а знаменатель на знаменатель.
    Пример - a/b * c/d = (a*c)/(b*d)
    Правило деления дробей - числитель первой умножаем на знаменатель второй, а знаменатель первой умножаем на числитель второй.
    Пример - a/b : c/d = (a*d)/(b*c)
    Правило сокращения дробей - в числителе и знаменателе должен быть общий множитель, на который и сокращается дробь.
    Пример (a*b)/(b*c) = a/c
    Десятичная дробь - в знаменателе число кратное 10 - 10, 100,1000 и др.
    Пример - 0,2 = 2/10 и 0,05 = 5/100 

  • Как выполнять действия с этими периодическими дробями(0,2(3) -0,1 или например, 9 11/15 - 0,2(6))?


    Решение: Как перевести периодическую дробь в обыкновенную:
    1) Считаем количество цифр в периоде десятичной дроби. Обозначаем количество цифр за букву k. У нас k=1.
    2) Считаем количество цифр, стоящих после запятой, но до периода десятичной дроби. Обозначаем количество цифр за букву m. У нас m=1.
    3) Записываем все цифры после запятой (включая цифры из периода) в виде натурального числа. Обозначаем полученное число буквой a. У нас а=23.
    4) Теперь записываем все цифры, стоящие после запятой, но до периода, в виде натурального числа. Обозначаем полученное число буквой b. У нас b=2.
    5) Подставляем найденные значения в формулу $$ Y+ \frac{a-b}{99.9000.0} $$, где Y — целая часть бесконечной периодической дроби (у нас Y=0), количество девяток равно k, количество нулей равно m.
    Вычислим примеры:
    1) $$ 0,2(3)-0,1=\frac{7}{30}-\frac{1}{10}=\frac{7-3}{30}=\frac{4}{30}=\frac{2}{15}=0,1(3) $$
    2) $$ 9\frac{11}{15}-\frac{4}{15}=\frac{146}{15}-\frac{4}{15}=\frac{131}{15}=8,7(3) $$

  • Как перевести неправильную дробь в обыкновенную или смешанную


    Решение: Чтобы из неправильной дроби выделить целую часть, надо:
    1) разделить с остатком числитель на знаменатель;
    2) неполное частное будет целой частью;
    3) остаток (если он есть) дает числитель, а делитель - знаменатель дробной части.
    Запись числа, содержащую целую и дробную части, называют смешанной. Для краткости вместо "число в смешанной записи" говорят смешанное число. Смешанное число можно представить и в виде неправильной дроби.
    Чтобы представить смешанное число в виде неправильной дроби, нужно:
    1) умножить его целую часть на знаменатель дробной части;
    2) к полученному произведению прибавить числитель дробной части;
    3) записать полученную сумму числителем дроби, а знаменатель дробной части оставить без изменения.

  • Как я могу перевести периодическую дробь в обыкновенную? Например: 1,58(3) и 9,1(6).
    Напишите правило и решение.


    Решение: Периодическую бесконечную десятичную дробь можно перевести в обыкновенную дробь. Рассмотрим периодическую дробь 10,0219(37). Считаем количество цифр в периоде десятичной дроби. Обозначаем количество цифр за букву k. У нас k = 2. Считаем количество цифр, стоящих после запятой, но до периода десятичной дроби. Обозначаем количество цифр за букву m. У нас m = 4. Записываем все цифры после запятой (включая цифры из периода) в виде натурального числа. Если вначале, до первой значащей цифры, идут нули, то отбрасываем их. Обозначаем полученное число буквой a.
    a = 021937 = 21 937
    Теперь записываем все цифры, стоящие после запятой, но до периода, в виде натурального числа. Если вначале до первой значащей цифры идут нули, то отбрасываем их. Обозначаем полученное число буквой b.
    b = 0219 = 219
    Подставляем найденные значения в формулу, где Y - целая часть бесконечной периодической дроби. У нас Y = 10.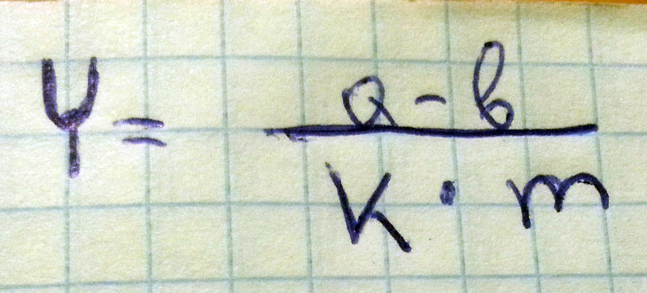

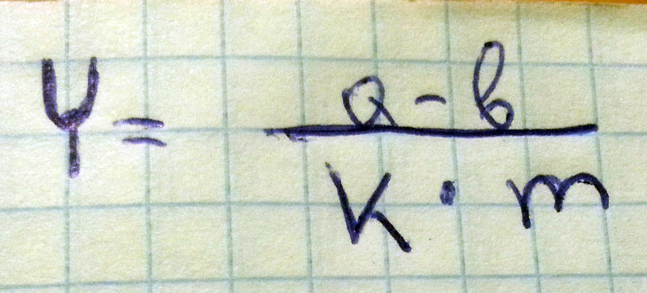
    Периодическую бесконечную десятичную дробь можно перевести в обыкновенную дробь. Рассмотрим периодическую дробь . Считаем количество цифр в периоде десятичной дроби. Обознача...
<< < 345 6 > >>