дроби »
перевести дробь в обыкновенную - страница 3
Как 14,4 перевести в обыкновенную дробь
Решение: У тебя написано: четырнадцать(14) целых и четыре(4) десятые. Если ты знаете дроби то ты в курсе про сотые, тысячные, десятые.
Переводим в обыкновенную: 14 целых оставляем без изменений. Далее 4 десятых "превращаем" в обыкновенную: сверху(в числителе) будет число 4 ( в данном случае); снизу: так как число 4 десятых и сверху у нас уже есть 4, то снизу(в знаменателе) уже будет 10(так как десятые)
ОТВЕТ: 14(целых) 4/10. Можно сократить на 2: 14(целых) 2/5Как перевести в обыкновенную дробь виде десятичной
Решение: 2 3/10*101=2,3*1,1=2,53
71/100*6,3=0,71*6,3=4,473
4 1/5*2,5=4,2*2,5=10,5
7 1/20=7,05*дальше не видноСмотри, у нас есть 2 3/10 (две целых три десятых) и 1,1 ( одна целая одна десятая). Что бы перевести десятичную др. нужно дамножить на то число что бы получилось : 10,100,1000. Так как у нас есть нижне число (извини забыла как называется ) и оно круглое (10) то записываем так как говорим :2,3
Перевести 4,(32) в обыкновенную дробь
Решение: 4,323232=x
1)1000x=4323,232
2)10x=43,232
затем отнимаете первое равенство от второго, у тебя получается:
990x=4280
x=4280/990
с помощью калькулятора сократи теперь правильно и все)Вот и все выше взято слишком большое кол во "Х"
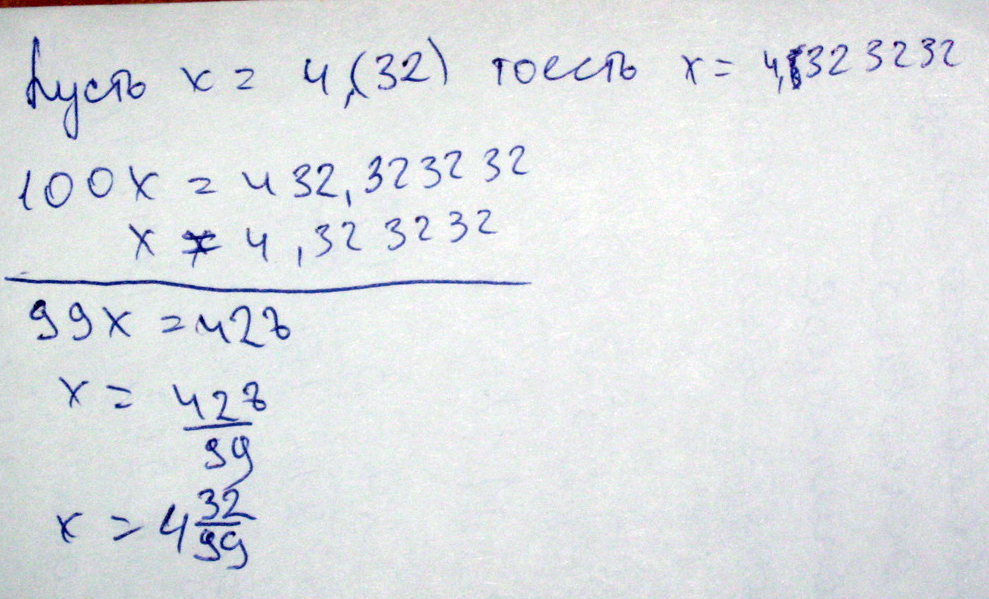
10,24 перевести в дробь обыкновенную
Решение: 10 целых и 24/100 или 1024/100
.$$ 10,24= 10\frac{24}{100}= 10\frac{24:4}{100:4}=10 \frac{6}{25} = \frac{25*10+6}{25} = \frac{256}{25} $$
Четвертая запись является смешанной дробью (присутствует в записи целая и дробная части).
Шестая запись является обыкновенной неправильной дробью (числитель больше знаменателя).перевести 0,(027) в обыкновенную дробь.
Решение: получится 27/1000. 0 целых означает, что целых чисел нет, а только дробные, поэтому перед дробью ничего не ставится. 27 означает часть от целой, а так как пишется 027, то значит двадцать семь тысячных. т. е. 27 в числитель-над чертой, а 1000 в знаменатель-под черту. получается 0, 027 - ноль целых, который не пишется в дробном виде, 27 тысячных - 27-я часть над чертой, 1000 под черту как тысячная часть от 27

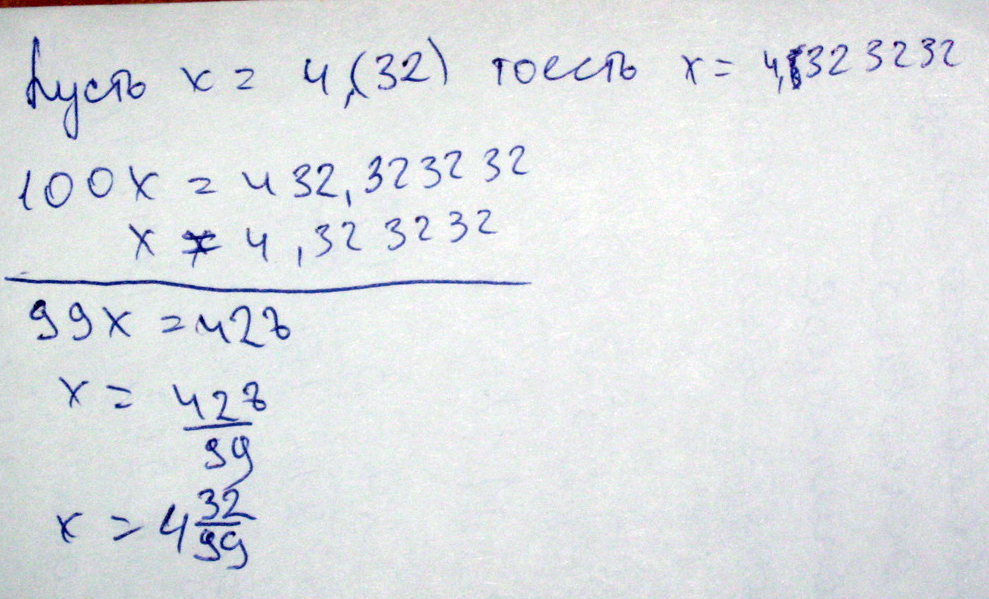
 Сложение и вычитание простых дробей
Для сложения и вычитания дробей с одинаковыми знаменателями нужно в первом случае сложить, а во втором вычесть их числители и результат сделать числителем новой дроби, а знаменатель подписать прежний.
Если знаменатели дробей различны, то нужно сначала привести все данные дроби к простейшему общему знаменателю.
При сложении или вычитании дробей с многочленными числителями и знаменателями в особенности важно...
Сложение и вычитание простых дробей
Для сложения и вычитания дробей с одинаковыми знаменателями нужно в первом случае сложить, а во втором вычесть их числители и результат сделать числителем новой дроби, а знаменатель подписать прежний.
Если знаменатели дробей различны, то нужно сначала привести все данные дроби к простейшему общему знаменателю.
При сложении или вычитании дробей с многочленными числителями и знаменателями в особенности важно...