дроби »

примеры с дробями

  • Выпиши пары дробей, которые ты можешь сравнить по величине: 3/9, 5/8, 4/7, 10/12, 7/8, 5/9, 7/15, 2/8, 2/3, 1/7, 5/6,2/9.запиши с ними верные неравенства.К остальным дробям подбери дроби, с которыми их можно сравнить. Запиши неравенства.


    Решение: 1)сравнить по величине....2/9 <3/9 <5/9 ````````````````2/8 <5/8 <7/`8```````````````1/7 <4/7``````````````2).подобрать дроби, с которыми можно сравнить-10/12 и5/6 (5/6 приводим к общему знаменателю и получаем 10/12).,значит 10/12=10/12........ 7/15и 2/3.........(2/3приводим к общему знаменателюи получаем 10/15),значит 7/15<10/15........................3) можно сравнить дроби с одинаковыми числителями:5/6>5/8> 5/9........7/8> 7/15...........2/3> 2/8> 2/9

    3/9 < 5/9, 3/9 > 2/9, 5/9 > 2/9
    5/8 < 7/8, 5/8 > 2/8, 7/8 > 2/8
    4/7 > 1/7
    10/12 = 5/6
    7/15 < 2/3



  • Нужно найти целые решения неравенства на отрезке [-3:3] Напишите подробное решение

    \( 3*9^x+11*3^x<4 \)


    Решение:

    $$ 3*9^x+11*3^x=4 $$

     $$ 3^x=t $$

     $$ 3t^2+11t-4=0 $$

     $$ t = \frac13 $$

     $$ t =-4 $$

     $$ 3^x=-4 $$ нет решений

     $$ 3^x=\frac13 $$

    $$ x =-1 $$

    Получаем ответ \( x=-1 \) целое решение на отрезке \( (-3,3) \)

  • 3(x-3)+2x-1
    ----------------- = 4x+1
    x-2


    ------ это черта дроби


    Решение: $$ \frac{3(x-3)+2x-1}{x-2}=4x+1 $$
    $$ \frac{3(x-3)+2x-1-(4x+1)(x-2)}{x-2}=0 $$
    $$ \frac{3x-9+2x-1-4x^2+8x-x+2}{x-2}=0 $$
    $$ \frac{-4x^2+12x-8}{x-2}=0 $$
    $$ \left[\begin{array}{ccc}-4x^2+12x-8=0\\x-2 eq 0\end{array}\right. $$
    $$ \left[\begin{array}{ccc}-4x^2+12x-8=0\\x eq 2\end{array}\right. $$
    $$ -4x^2+12x-8=0 $$
    $$ D=12^2-4*(-4)*(-8)=144-128=16 $$
    $$ x_{1}= \frac{-12-4}{2*(-4)}= \frac{-16}{-8}=2 $$ - не является корнем уравнения
    $$ x_{2}= \frac{-12+4}{2*(-4)}= \frac{-8}{-8}=1 $$
    Ответ: х=1

  • Представьте степень с дробным показателем в виде корня: а) 3 в степени 1/2; 5 в степени 3/4; 0,2 в степени 0,5; 7 в степени -0,25. б) х в степени 3/4; а в степени 1,2; b в степени -0.8; с в степени 8/3. в) 5а в степени 1/3; ах в степени 3/5; -b в степени -1,5; (2b) в степени 1/4. г)(х-у) в степени 2/3; х в степени 2/3 - у в степени 2/3; 3(а+b) в степени 3/4; 4а в степени -2/3 + ах в степени 2/3.


    Решение: a)$$ 3^{\frac{1}{2}} = \sqrt{3} $$

    $$ 5^{\frac{3}{4}} = \sqrt[4]{5^3}=\sqrt[4]{125} $$

    $$ 0.2^{0.5}=\sqrt{0.2} $$

    $$ 7^{-0.25}=\frac{1}{7^{0.25}}=\frac{1}{\sqrt[4]{7}}=\sqrt[4]{\frac{1}{7}} $$

    б) $$ x^{\frac{3}{4}} = \sqrt[4]{x^3} $$

    $$ a^{1.2} = a^{\frac{6}{5}} = \sqrt[5]{a^6}=a \sqrt[5]{a} $$

    $$ b^{-0.8} = \frac{1}{b^{0.8}}=\frac{1}{\sqrt[5]{b^4}}=\sqrt[5]{\frac{1}{b^4}} $$

    $$ c^{\frac{8}{3}} = \sqrt[3]{c^8}=c^2\sqrt[3]{c^2} $$

    в) $$ 5a^{\frac{1}{3}} = \sqrt[3]{5a} $$

    $$ (ax)^{\frac{3}{5}} = \sqrt[5]{(ax)^3} $$

    $$ -b^{-1.5} = -b^{-\frac{3}{2}} = \frac{1}{\sqrt{(-b)^3}} $$

    $$ (2b)^{\frac{1}{4}} = \sqrt[4]{2b} $$

    г) $$ (x-y)^{\frac{2}{3}} = \sqrt[3]{(x-y)^2} $$

    $$ x^{\frac{2}{3}}-y^{\frac{2}{3}} = \sqrt[3]{x^2}-\sqrt[3]{y^2} $$

    $$ 3(a+b)^{\frac{3}{4}} = 3\sqrt[4]{(a+b)^3} $$

    $$ 4a^{-\frac{2}{3}}+ax^{\frac{2}{3}} = \frac{4}{\sqrt[3]{a^2}}+a\sqrt[3]{x^2} $$

  • Представьте в виде корня (b 5\3*b 4\3)3\2 5\3 4\3 3\2 это степень \\ этот знак дроби


    Решение:

    ===============

    $$ b^\frac{5}{3}=\sqrt[3]{b^5} $$

    $$ b^\frac{4}{3}=\sqrt[3]{b^4} $$

    в итоге

    $$ \sqrt[2]{(\sqrt[3]{b^5}*\sqrt[3]{b^4})^3}=\sqrt[2]{\sqrt[3]{b^5*b^4}^3}=\\=\sqrt{b^5*b^4}=\sqrt{b^9}=4b\sqrt{b} $$

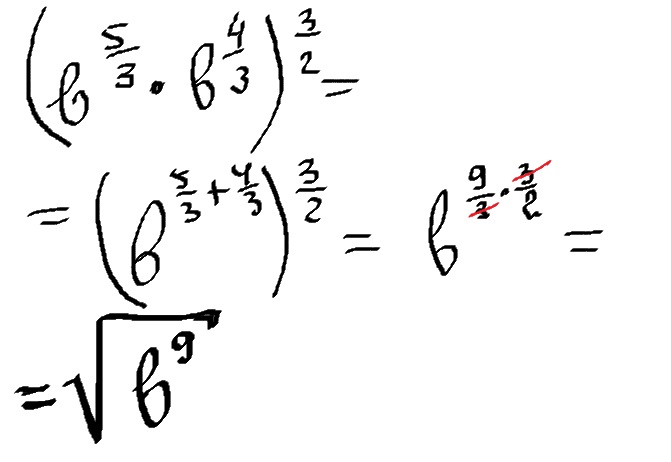
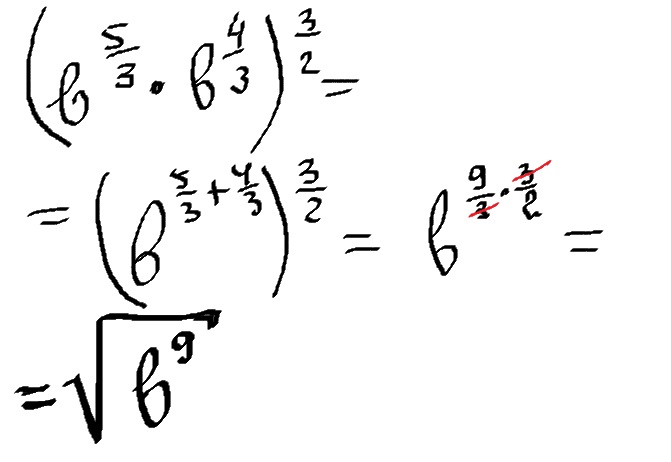
    b frac sqrt b b frac sqrt b в итоге sqrt sqrt b sqrt b sqrt sqrt b b sqrt b b sqrt b b sqrt b...
1 2 3 > >>