график функции производной - страница 19
Исследовать функцию с помощью производной и построить ее график f(x)=4x^3-6x^2
Решение: Производная функции f(x)=4x^3-6x^2 равна:
f ’(x) = 12x² - 12x.Исследовать функцию f (x) = 4x³–6x² и построить ее график.
Решение:
1. Область определения функции - вся числовая ось.
2. Функция f (x) = 4x³–6x² непрерывна на всей области определения. Точек разрыва нет.
3. Четность, нечетность, периодичность:
График четной функции симметричен относительно оси ОУ, а нечетной — относительно начала координат О.
f(–x) = 4(–x)³–6(–x)² = –(4x³+6x²) ≠ –f(x),
f(–x) = 4(–x)³3–6(–x)² = –(4x³+6x²) ≠ –f(x)
Функция не является ни четной, ни нечетной. Функция непериодическая.
4. Точки пересечения с осями координат:
Ox: y=0, 4x³–6x²=0, 2x²(2x–3)=0 ⇒ x=0, x=3/2. Значит (0;3/2), точки пересечения с осью Ox.
Oy: x = 0 ⇒ y = 0. Значит (0;0) - точка пересечения с осью Oy.
5. Промежутки монотонности и точки экстремума:
y’=0 ⇒ 12x²–12x =0 ⇒ 12x(x–1) = 0 ⇒ x = 0, x = 1 - критические точки.
Если производная положительна - функция возрастает, если производная отрицательна - функция убывает:
отрезок -∞ < x < 0 функция возрастает,
отрезок 0 < x < 3/2 функция убывает,
отрезок 3/2 < X < ∞ функция возрастает.
7*. Вычисление второй производной: у =4x³–6x²,
f ’(x) = 12x² - 12x. f ’’(x) = 24x - 12.
y’’=0, 24x–12= 0, x = 12/24 = 1/2.
8*. Промежутки выпуклости и точки перегиба:
отрезок -∞ < x < 1/2 график функции выпуклый вверх,
точка перегиба х = 1/2,
отрезок 1/2< x < ∞ график функции выпуклый вниз.
9. Найдем значение функции в дополнительной точке: f(1/2) = 4*(1/2)³– 6(1/2)² = 4/8 -6/4 = (4-12) / 8 = -8/8 = –1.
10. Искомый график функции .
Исследовать функцию с помощью производной и построить ее график : y=x^2 + 2/x
Решение:
Найдём производную у = 2х+2,
найдём критические точки, решив уравнение 2х + 2 = 0, х = - 1,
найдём знак производной на промежутках: у( -2) = -4+2 = - 2, то на
( -∞ ; - 1) производная отрицательна, значит функция на этом промежутке убывает;
у (3) = 6+2=8, то на (- 1; ∞ ) производная положительна, значит функция возрастает.
Найдём координату точки минимума у( -1) = - 2 + 2 = 0
Графиком будет парабола с вершиной в точке ( - 1; 0)Найдите значения х, при которых значения производной функции f(x) равно 0, если: f(x)= 4x^3 - x^2 - 2x
Напишите уравнение касательной к графику функции y=f(x) в его точке с абсциссой х нуливое, если: f(x)=2x^2 - x + 2, x нулевое=-1
РЕШИТЕНАДО
Решение: $$ \\f(x)= 4x^3 - x^2 - 2x\\ f’(x)=12x^2-2x-2\\ 12x^2-2x-2=0\\ 6x^2-x-1=0\\ \Delta=(-1)^2-4\cdot6\cdot(-1)\\ \Delta=1+24\\ \Delta=25\\ \sqrt{\Delta}=5\\ \\x_1=\frac{-(-1)-5}{2\cdot6}\\ x_1=\frac{-4}{12}\\ x_1=-\frac{1}{3}\\\\ x_2=\frac{-(-1)+5}{2\cdot6}\\ x_2=\frac{6}{12}\\ x_2=\frac{1}{2}\\\\ \\ \\y=f’(x_0)(x-x_0)+f(x_0)\\ f(-1)=2\cdot (-1)^2 - (-1) + 2\\ f(-1)=2+3\\ f(-1)=5\\ f’(x)=4x-1\\ f’(-1)=4\cdot (-1)-1\\ f’(-1)=-4-1\\ f’(-1)=-5\\\\ y=-5(x-(-1))+5\\ y=-5(x+1)+5\\ y=-5x-5+5\\ y=-5x $$Решить
1) Записать уравнение касатальной к графику функции f(x)=4x-sinx+1 в точке x0=0
2) найти значения x, при которых значения производной функции f(x)=(1-x)/(x^2+8) отрицательны
Решение: 1) Производная функции f(x)=4x-sinx+1 равна f’(x) = 4 - cos(x).
Значения функции и производной в заданной точке Хо = 0 равны:
f(0) = 4*0 - 0 + 1 = 1
f’(x) = 4 - 1 = 3
Тогда уравнение касательной:
Укас = 1 + 3*(Х - 0) = 3Х + 1.
2) Производная функции f(x) = (1 - x) / (x^2 + 8) равна:
f’(x) = (x^2 - 2x - 8) / (x^2 + 8)^2.
Так как в знаменателе квадрат, то отрицательной производная может быть при отрицательном числителе.
Для этого находим критические точки:
x^2 - 2x - 8 = 0
Квадратное уравнение, решаем относительно x:
Ищем дискриминант:D=(-2)^2-4*1*(-8)=4-4*(-8)=4-(-4*8)=4-(-32)=4+32=36;
Дискриминант больше 0, уравнение имеет 2 корня:
x_1=(√36-(-2))/(2*1)=(6-(-2))/2=(6+2)/2=8/2=4;
x_2=(-√36-(-2))/(2*1)=(-6-(-2))/2=(-6+2)/2=-4/2=-2.
Поэтому ответ: f’(x) < 0 при -2 <x < 4.F(x) = 3x^2-x^3-1 Исследовать функцию с помощью производной и построить ее график. кому не лень
Решение: D(f)∈(-∞;∞)
f(-x)=3x²+x³-1 ни четная, ни нечетная
f’(x)=6x-3x²=-3x(x-2)=0
x=0 x=2
_ + _
-(0)-(2)-
убыв min возр max убыв
ymin=-1
ymax=12-8-1=3
f’’(x)=6-6x=0
x=1 y=3-1-1=1
(1;1)-точка перегиба
+ _
-(1)-
вог вниз вып вверх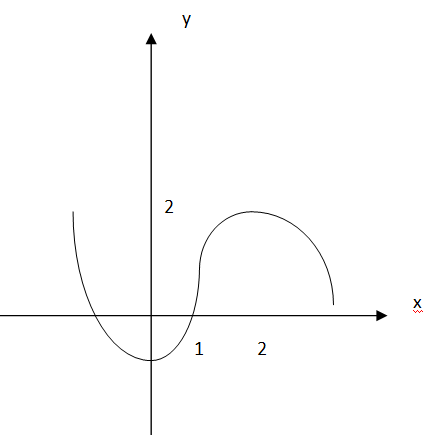

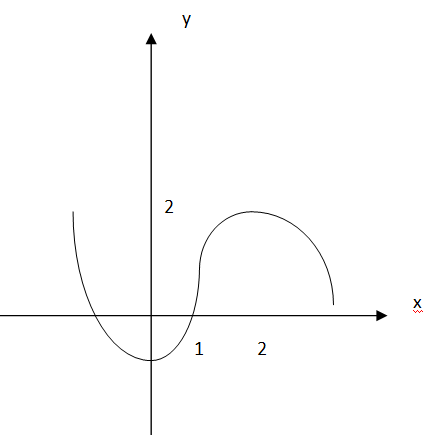
 Допустим, есть некоторая функция s (t), указывающая путь, пройденный телом за время от 0 до t. Аргументу t дается некоторое приращение τ, то есть вместо значения t рассматривается значение t + τ. Этому приращению аргумента соответствует следующее приращение функции s (t):
s (t + τ) - s (t).
Это приращение функции делится на приращение аргумента τ
s (t + τ) - s (t)τ
и...
Допустим, есть некоторая функция s (t), указывающая путь, пройденный телом за время от 0 до t. Аргументу t дается некоторое приращение τ, то есть вместо значения t рассматривается значение t + τ. Этому приращению аргумента соответствует следующее приращение функции s (t):
s (t + τ) - s (t).
Это приращение функции делится на приращение аргумента τ
s (t + τ) - s (t)τ
и...