график функции производной - страница 20
Ребят а то не допуск по математике;(((
Исследуйте функцию с помощью производной и постройте её график:
y=4x-x^2
Решение: Всё подробно написала в решении.1. D(f)= R
2. Нули функции а) график пересекает ось Ох, у=0, тогда 4х-х^2=0
x(4-x)=0
x=0 или x=4. точки пересечения по оси Ох ( 0;0) и (4;0)
б) график пересекает ось Оу, если х=0, тогда у=0 точка пересечения с Оу ( 0;0)
3. Производная равна у/= 4-2x. по т Ферма
4-2х=0
2х=4
х=2, если х=2, то у= 4*2-2^2=4 получим точку вершины параболы ( 2;4)
4/ Ветви параболы направлены вниз, тк а=-1
5. ( - бескон. 2) функция возрастает, ( 2: + бесконеч) функция убывает
max f(x)=f(2)=4
по данным точкам построй параболу.
Решите 1) Прямая проходящая через точку А(-6;1) касается графика функции у=F(x) в точке (-2;4). Найдите значение производной функции в точке х=-2
Ответ:0,75
2) Если автомобиль, имеющий скорость V0(м/с), осуществляет торможение с постоянным ускорением a (м/с^2), a<0, то время t ( в секундах), прошедшее с
момента начала торможения до момента полной остановки автомобиля, определяется формулой t=V0/ |a|. Какую наименьшую скорость мог иметь автомобиль, если при a= -8 м/с^2 время от начала торможения до момента полной остановки составило не менее 5 секунд?
Ответ:144
Решение: 1) Попробуем написать уравнение касательной. касательная - это прямая. Уравнение прямой в общем виде : у = кх + b. х и у - это координаты точек, через которые наша касательная проходит.
1 = -6к +b
4 = -2k+ b вычтем из 2-го уравнения первое, получим: 3 = 4к, к = 3/4. к - это угловой коэффициент касательной, а угловой коэффициент - это производная в точке касания. Ответ: 3/4 = 0,75Математики, я знаю, что для вас это сущий пустяк))
1) Найдите значение производной функции f(x)=x^3 - 4 в точке в точке хо=2
2) Запишите уравнение касательной к графику функции f(x)=cos^2 x в точке с абсциссой хо=П\2
Решение: 1) f’(x)=3x^2;f’(x0)=3*4=12
2) f(pi/2)=y0=0;
f(x)=(1+cos2x)/2
f’(x)=-sin2x
k=f’(pi/2)=0
ур-е кас y=y0+k(x-x0)
y=0
1)$$ f’(x)=(x^3)’-(4)’=3x^2\\f’(x_{0})=f’(2)=3*2^2=12 $$
2) Уравнение касательной:$$ y=f’(x_{0})(x-x_{0})+f(x_{0}) $$
Производная:
$$ f’(x)=(cos^2x)’=(cosx*cosx)’=\\=(cosx)’*cosx+cosx*(cosx)’=\\=(-sinx)*cosx+cosx*(-sinx)=-sinx*2cosx=-2sin2x. $$
Или можно проще:
$$ f’(x)=(cos^2x)’*(cosx)’=2cosx*-sinx=-2sin2x \\ f’(x_{0})=f’(\frac{\pi}{2})=-2sin(\frac{2*\pi}{2})=-2sin180=0 \\ f(x_{0})=f(\frac{\pi}{2})=cos^2(\frac{\pi}{2})=cos^290=0 $$
Подставим значения в уравнение касательной:
$$ y=0*(x-\frac{\pi}{2})+0=0 $$
,
Завтра сдавать, а у меня нет решения :( пнкт не жалею
1. Найти значение производной функции f(x)=2x^3+3x^2-x в точке х=-2.
2. Найти производную функции:
1) 2/x +4sqrt{х} - e^x 2)(3x-5)^3
3) 3sin2x*cosx 4) (x^3)/(x^2+5)
3. Найти угол между касательной к графику функции y=x^4-2x^3+3 в точке с абсциссой х0=1/2 и осью Ох.
4. Найти значения х, при которых значения функции f(x)=ln(3x+1) отрицательны.
5. Напишите уравнение касательной к графику функции y=1/3 x^3 - x^2 +5 которая параллельна прямой y=3x-2.
Решение: Все, что смогла.1. $$ 6*x^2+6*x-1 $$ производная
$$ 6*(-2)^2+6*(-2)-1=11 $$
2.
1)$$ - \frac{2}{x^2} - \frac{2}{ \sqrt{x} } -e^x $$
2)$$ 3*(3*x-5)^2*3=9*(3*x-5)^2 $$
3)$$ 6*cos(2x)*cos(x)+3*sin(2x)*sin(x) $$
4)$$ \frac{2*x^2*(x^2+5)-x^3*2*x}{(x^2+5)^2} $$
3.$$ 4*x^3-6*x^2 $$ производная
$$ y(1/2)= 4*(1/2)^3-6*(1/2)^2=-1 $$
4. По графику, от нуля до точки разрыва х = -0.32
5. $$ x^2-2*x=3 $$ производную функции приравниваем к 3, т. к угловой коэффициент прямой y=3*x-2 равен 3. Дальше находим значение x и его подставляем в исходное уравнение y=1/3*x^3-x^2+5 получаем y=5,
Искомое уравнение принимает вид y=k*x+b, b=-4 (подставив значение y=5 x=3)
Искомое уравнение имеет вид y=3*x-4
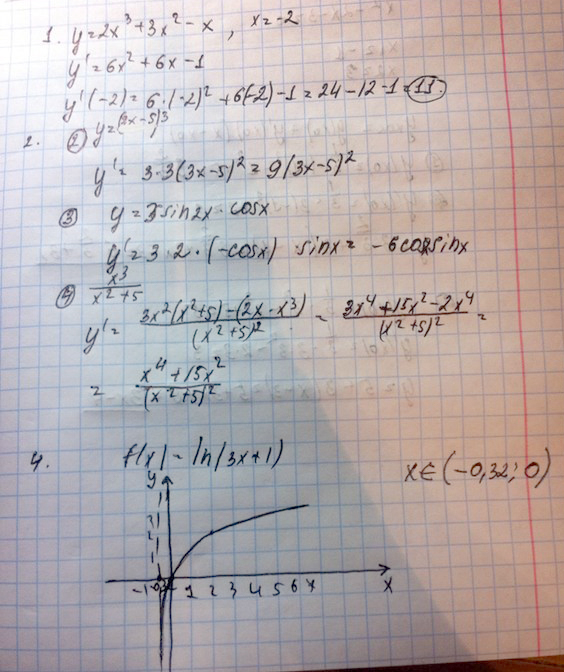
А1. Из пункта А в пункт В, расстояние между которыми 60 км, одновременно выехали автомобилист и велосипедист. Известно, что в час автомобилист проезжает на 35 км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт В на 2 часа 48 минут позже автомобилиста. Ответ дайте в км/ч. 1) 20 2) 15 3) 10
— производной функции
, определенной на интервале
. Найдите количество точек, в которых касательная к графику
функции
параллельна прямой
или совпадает с ней.
1)
1 2) 3 3) 4
Решение: Пусть x км/ч - скорость велосип. тогда (х+35) км/ч - скорость автом.
составим уравнение:
2 часа 48 минут = 2,8часа
$$ \frac{60}{x} = \frac{60}{x+35} +2.8 $$
60(x+35) = 60x + 2.8x(x+35)
60x + 2100 = 60x + 2.8x² + 98x
2.8x² + 98x - 2100 = 0
1.4x² + 49x - 1050 = 0
D = 2401+5880=8281
x₁ = (-49+91) / 2.8 = 15
x₂ = (-49-91) /2 <0 не удов.
Ответ: 15 км/ч


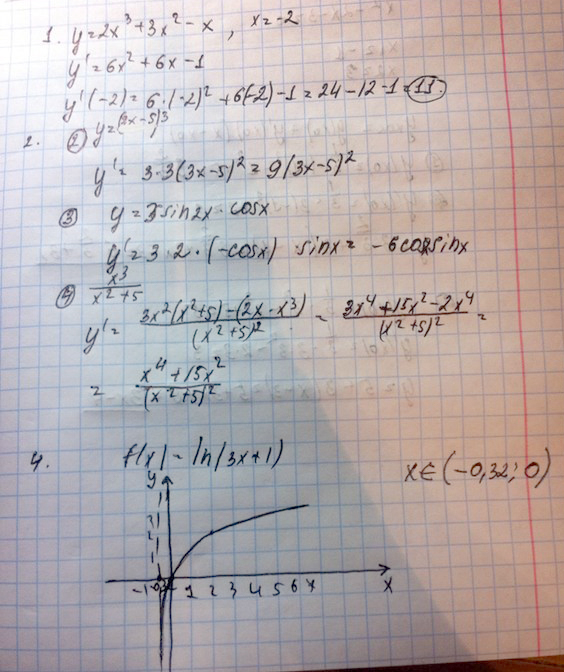
 Допустим, есть некоторая функция s (t), указывающая путь, пройденный телом за время от 0 до t. Аргументу t дается некоторое приращение τ, то есть вместо значения t рассматривается значение t + τ. Этому приращению аргумента соответствует следующее приращение функции s (t):
s (t + τ) - s (t).
Это приращение функции делится на приращение аргумента τ
s (t + τ) - s (t)τ
и...
Допустим, есть некоторая функция s (t), указывающая путь, пройденный телом за время от 0 до t. Аргументу t дается некоторое приращение τ, то есть вместо значения t рассматривается значение t + τ. Этому приращению аргумента соответствует следующее приращение функции s (t):
s (t + τ) - s (t).
Это приращение функции делится на приращение аргумента τ
s (t + τ) - s (t)τ
и...