производная »

график функции производной - страница 18

  • Исследуйте функцию с помощью производной и постройте её график:
    f(x)=4x^4-16/3x^3.


    Решение: $$ f(x)=4x^{4}- \frac{16}{3x^{3}}; \\ f’(x)=16x^{3}- \frac{(16)’*3x^{3}-(3x^{3})’*16}{(3x^{3})^{2}}= \\ \frac{0*3x^{3}-9x^{2}*16}{3x^{6}}= \\ -\frac{144x^{2}}{3x^{6}}. \\ f’(x)=0 \\ -\frac{144x^{2}}{3x^{6}}=0 \\ 3x^{6} = 0 \\ x = 0 $$f x x - frac x f x x - frac x - x x frac x - x x - frac x x . f x - frac x x x x...

  • Исследуйте функцию с помощью производной и постройте её график f(x)=x3-x2+4


    Решение: 1)D(y)=R

    2)f’(x)=3x2-2x

    3)y=0,3x2-2x=0

    x=0 или 3x-2=0

      x=1.5 

    4)x=0, y=0.

      (-∞;0) 0  (0;1.5) 1.5  (1.5;+∞)

    f’(x) + 0  - 3.75  +

    f(x) возрастает 4  убывает 12.875  возрастает

    минимум 

  • Исследовать функцию с помощью производной и построить её график. y=1/3x^2 - 1/2x^2


    Решение: 1) область определения: -∞,+∞
    2) область значения: -бесконеччность,+∞
    3) пересечение с осью Ox: (0,0); (3/2,0)
    4) экстремумы и монотонность: y’=x^2-x
    x^2-x=0
    x=0 и x=1
    (-∞,0) и (1,+∞) функция возрастает
    (0,1) функция убывает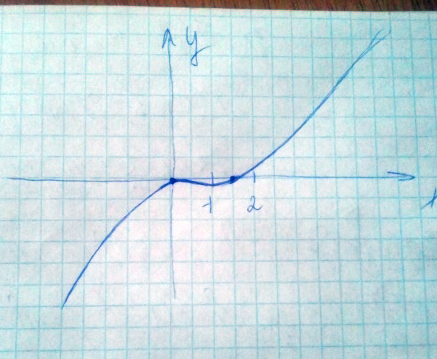

    область определения - область значения -бесконеччность пересечение с осью Ox экстремумы и монотонность y x -xx -x x и x - и функция возрастает функция убывает...

  • Исследовать функцию с помощью производной и построить ее график: у=2х2-5х+2.


    Решение: Найдём производную у = 2х+2, 
    найдём критические точки, решив уравнение 2х + 2 = 0, х = - 1, 
    найдём знак производной на промежутках: у( -2) = -4+2 = - 2, то на 
    ( -∞ ; - 1) производная отрицательна, значит функция на этом промежутке убывает;
    у (3) = 6+2=8, то на (- 1; ∞ ) производная положительна, значит функция возрастает.
    Найдём координату точки минимума у( -1) = - 2 + 2 = 0
    Графиком будет парабола с вершиной в точке ( - 1; 0)

  • Исследовать функцию с помощью производной и построить ее график
    y = x^3/2 + 3x^2 + 1


    Решение: Y=x³/2+3x²+1
    D(y)∈(-∞;∞)
    y(-x)=-x³/3+3x²+1 ни четная и ни нечетная
    y’=3x²/2+6x=0
    1,5x(x+4)=0
    x=0  x=-4
       +  _  +
    -(-4)-(0)-
    возр  max  убыв  min  возр
     ymax=y(-4)=-32+48+1=17
    ymin=y(0)=1
    y’’=3x+6=0
    x=-2
    y(-2)=-4+12+1=9
    (-2;9)-точка перегиба
       _  +
    -(-2)-
    выпук вверх  вогн вниз
    -
<< < 161718 19 20 > >>