график функции производной - страница 16
Исследовать функцию с помощью производной и построить график y=3x-3^3
Решение: Y=(3x-3)^3
y’=9(3x-3)^2
y’=0
3x-3=0
X=1
Чертим ось х. Сверху слева над осью пишем у’ снизу слева под осью просто у. Ставим точку 1. Определяем знаки производной. Выходит + и +, в обоих промежутках, делаем вывод: функция не имеет экстреммумов и всегда возрастает. График- кубическая парабола, идёт снизу вверх пересекает ось х в точке 1.Исследовать функцию с помощью производной и построить график
Решение: 1) D(y)=R;E(y)=R
2)F(-x)=-1/6*x^3+12x функция нечетная3) Точки пересечений:
Ох: x(1/6*x^2-12)=0
x=0 ; x^2=72
x=+-\sqrt72
Oy: y=0
4)f`(x)=x^2/2-12=0
x=+-\sqrt(24)
ф-я возрастает от (-беск.\sqrt(24));(sqrt(24);+беск.)
ф-я убывает от (-\sqrt(24);sqrt(24)
x(max)=-\sqrt(24) x(min)=\sqrt24
5) Точки перегиба:
f``(x)=(1/6*x^3-12*x)=x=0
Т. пер: х=0()
У нас в школе обычно так описывали функцию. Извиняюсь за сколь "корявое описание" просто в редакторе писать долго. а сам график . Да и еще недочет в том что из под корней можно вытащить числа.
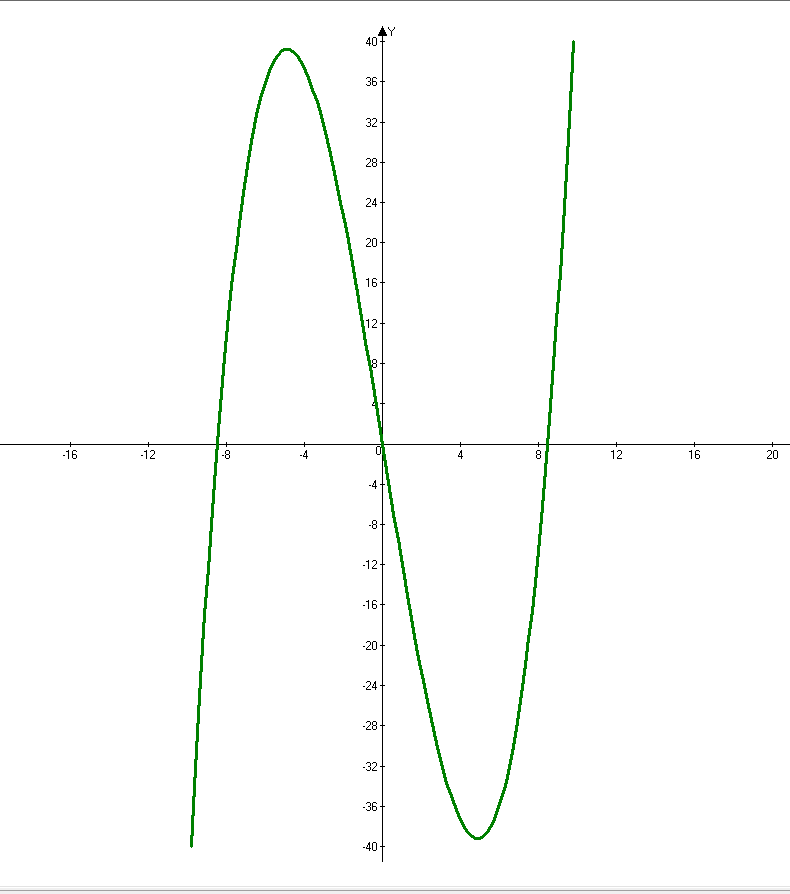
$$ f(x) = \frac{1}{6}x^3 - 12x \\ 1) $$ Функция определена и непрерывна на множестве вещественных чисел $$ R \\ 2) \ f’(x) = \frac{1}{2}x^2 - 12\\\\ \frac{1}{2}x^2 - 12 = 0\\\\ \frac{1}{2}x^2 = 12\\\\ x^2 = 24\\\\ \boxed{ x_1 = -\sqrt{24}, \ x_2 = \sqrt{24} } $$
Так как это парабола, ветви которой идут вверх, то она будет принимать отрицательные значения при $$ x \in (-\sqrt{24};\sqrt{24}). $$ Соответственно исходная функция будет убывать при $$ x \in (-\sqrt{24};\sqrt{24}) $$ и возрастать при $$ x \in (-\infty; -\sqrt{24}) \cup (\sqrt{24}; +\infty) \\ 3) \ \min\limits_{x} f(x) = f(\sqrt{24}) = -16\sqrt{6}\\\\ \max\limits_{x} f(x) = f(-\sqrt{24}) = 16\sqrt{6} \\ 4) f(x) = \frac{1}{6}x^3 - 12 = 0\\\\ x(\frac{1}{6}x^2 - 12) = 0\\\\ \frac{1}{6}x(x^2 - 72) = 0\\\\ \boxed{x_1 = 0, \ x_2 = -\sqrt{72}, \ x_3 = \sqrt{72}} $$
Исследуйте функцию с помощью производной и постройте график Y=2-3x^2-x^3
Решение: D/dx ( 2 - 3x^2 - x^3) = -3x(x+2)
Тогда max( y = 2- 3x^2 - x^3=)2, x = 0( локальный максимум)
И min(y = 2- 3x^2 - x^3) = - 2, x = -2 (локальный минимум)Построение графика функции с помощью производной \(y=\frac{x+1}{x^2+1}\)
Решение: Попробуем исследовать в меру возможного.
1) Область определения.
X⊂ R или Х ⊂ (-∞;+∞)
2) Непрерывная. Разрывов нет.
3) На четность. У(1) = 2/5 и У(-1) = 0. Функция ни четная, ни нечетная.
4) Пересечение с осью Х при Х= -1.
Пересечение с осью У при Х=0 У=1
5) Асимптоты. Lim(-∞) = 0. Lim(+∞) = 0.
6) Монотонность.
Производная
$$ Y’= \frac{1}{ x^{2} +1}- \frac{2x(x+1)}{ ( x^{2} +1)^{2} } $$
Убывает - Х⊂(-∞,√2-1]∪[√2-1,+∞)
Возрастает - X⊂[-√2-1,√2-1]
Точки экстремума.
$$ Ymin =- \frac{ \sqrt{2} }{(- \sqrt{2}-1 ) ^{2}+1 } \\ Ymax= \frac{ \sqrt{2} }{( \sqrt{2}-1 )^{2}+1 } $$
График, конечно, приблизительный.Исследовать функцию с помощью производной и построить график f(x)=x^4-6x^2+4 отрезок от -1 до 1
Решение: Дана функция: f(x)=x^4-6x^2+4.Общая схема исследования и построения графика функции
1. Найти область определения функции и область значений функции, выявить точки разрыва, если они есть.
Область определения функции D(x)( = R.
При определении области значений функции задача сводится к нахождению наибольшего и наименьшего значения функции (это будет в пункте 8).
2. Выяснить, является ли функция четной или нечетной.
Проверим функцию чётна или нечётна с помощью соотношений f = f(-x) и f = -f(-x).
(-x)^4-6*(-x)^2+4 = x^4-6x^2+4.
То есть, f = f(-x). Функция чётная.3. Выяснить, является ли функция периодической - нет.
4. Найти точки пересечения графика с осями координат (нули функции).
График функции пересекает ось X при f = 0
x^4−6x^2+4=0.
значит надо решить уравнение:
Замена: х^2 = t.
Имеем квадратное уравнение t^2-6t+4=0
Квадратное уравнение, решаем относительно t:
Ищем дискриминант:D=(-6)^2-4*1*4=36-4*4=36-16=20;
Дискриминант больше 0, уравнение имеет 2 корня:t_1=(√20-(-6))/(2*1)=(√20+6)/2=√20/2+6/2=√20/2+3 =
= √5 + 3 ≈ 5.236068;t_2=(-√20-(-6))/(2*1)=(-√20+6)/2=-√20/2+6/2=-√20/2+3 =
= -√5 + 3 ≈ 0.763932.
Тогда получаем 4 корня:
х_1 = -(-√5 + 3),
х_2 = √(-√5 + 3),
х_3 = -√(√5 + 3),
х_4 = √(√5 + 3). Точки пересечения с осью X:
Численное решение
x1=0.874032048898,
x2=−0.874032048898x2,x3=−2.28824561127,
x4=2.28824561127.
График пересекает ось Y, когда x равняется 0:
подставляем x = 0 в x^4 - 6*x^2 + 4.
0^4−0+4 = 4Результат:
f(0)=4
Точка:
(0, 4)5. Найти асимптоты графика - их нет.
6. Вычислить производную функции f’(x) и определить критические точки.
f’(x) = 4х³ - 12х = 4х(х² - 3).
Приравниваем производную нулю: 4х(х² - 3) = 0.
Получаем 3 корня (это критические точки):
х = 0, х = √3 и х = -√3.
7. Найти промежутки монотонности функции.
Исследуем знаки производной:
х = -2 -1.732 -1.5 -0.5 0 0.5 1.5 1.732 2
y’=4х³ - 12х -8 0 4.5 5.5 0 -5.5 -4.5 0 8.
Где производная положительна - там функция возрастает, где отрицательна - там функция убывает.
Возрастает на промежутках [-sqrt(3), 0] U [sqrt(3), oo).
Убывает на промежутках (-oo,sqrt(3)] U [0, sqrt(3)]8. Определить экстремумы функции f(x).
Где производная меняет знак с - на + там минимум функции, где меняет знак с + на - там максимум.
экстремумы в точках:
(0, 4) максимум,(-√ 3,5) и (√ 3,5) минимумы.
9. Вычислить вторую производную f’’(x).
Приравниваем нулю вторую производную:
f’’(x) = 12х²-12 =12(х² - 1) = 0.
Имеем 2 точки перегиба функции: х = 1 и х = -1.
10. Определить направление выпуклости графика и точки перегиба.
Вогнутая на промежутках (-oo,1] U [1, oo).
Выпуклая на промежутках [-1, 1]11. Построить график, используя полученные результаты исследования - .
На заданном интервале графика от -1 до 1 будет только выпуклая его часть.
Допустим, есть некоторая функция s (t), указывающая путь, пройденный телом за время от 0 до t. Аргументу t дается некоторое приращение τ, то есть вместо значения t рассматривается значение t + τ. Этому приращению аргумента соответствует следующее приращение функции s (t):
s (t + τ) - s (t).
Это приращение функции делится на приращение аргумента τ
s (t + τ) - s (t)τ
и...