производная »

график функции производной - страница 14

  • На рисунке изображен график функции, к которому проведены касательные в четырех точках.
    Ниже указаны значения производной в данных точках. Пользуясь графиком, поставьте в соответствие каждой точке значение производной.


    Решение: 6) Углы наклона в точках А и D - тупые, причем угол А меньше угла D.
    Тангенсы углов (от 90 до 180) во второй четверти- отрицательные.
    Тангенс функция возрастающая, меньшему углу соответствует меньшее значение тангенса
    О т в е т.
    В точке А  3); в точке В 2) в точке С 4) в точке D 1).
    Аналогично,
    7) О т в е т.
    в точке А 2); в точке В 4); в точке С 1); в точке D  3).
    8) О т в е т.
    в точке K 2); в точке L 4); в точке M 1); в точке N  3).

  • На рисунке изображён график функции, к которому проведены касательные
    в четырёх точках.
    Ниже указаны значения производной в данных точках. Пользуясь графиком,
    поставьте в соответствие каждой точке значение производной в ней.
    ТОЧКИ:
    А )K
    Б) L
    В) M
    Г) N
    ЗНАЧЕНИЯ ПРОИЗВОДНОЙ:
    1)−4
    2) 3
    3) 2/3
    4) −0,5


    Решение: Геометрический смысл производной в точке
    f`(x₀)= k (касательной)
    k(касательной)=tgα, α - угол наклона касательной (прямой) к оси ох.
    Так как функция тангенс возрастает на (-π/2; π/2), то большему значению  аргумента соответствует большее значение тангенса.
    угол 1 и угол 2 образуют острые углы с осью ох. Тангенс острого угла положителен.
    Угол 2 больше угла 1, значит углу 2 соответствует значение производной равное 3, а углу 1 соответствует значение производной, равное 2/3.
    Углы 3 и 4 тупые. А смежные к ним острые.
    Смежный углу 3 больше, чем смежный к углу 4. Значит, тангенс  смежного с углом 3  равен |-4|=4, угол 3 имеет тангенс, равный (-4) и значение производной соответственно (-4).
    См. рисунок .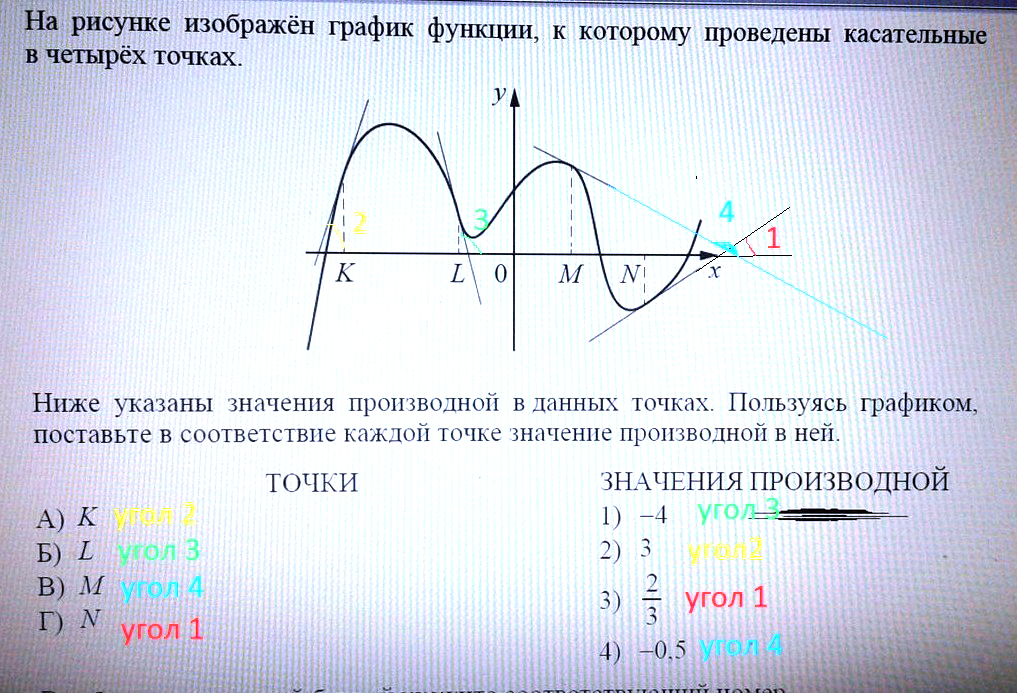

    Геометрический смысл производной в точкеf x k касательной k касательной tg - угол наклона касательной прямой к оси ох.Так как функция тангенс возрастает на - то большему знач...

  • На рисунке изображен график функции, к которой проведены касательные в четырех точках. Ниже указаны значения производной в данных точках. Пользуясь графиком, поставьте в соответствие каждой точке значение производной.


    Решение: Производная убывающей функции отрицательна: чем быстрее функция убывает, тем значение производной по модулю будет больше; следовательно, в точках A и D производная будет отрицательна, т. к. в точке A функция быстрее убывает, значит производная в этой точке будет равна -1 3/4, а в точке D -2/3. В точках B и C функция возрастает, значит значение производной будет положительное, а именно в точке B она будет равна 1,4, а в точке C 0,5, т. к. в точке C функция возрастает медленее

  • 1) Упростите выражение.
    2) На рисунке изображен график к функций y=f(x) и касательная к нему в точке с абсциссой х0. Найдите значение производной в точке х0


    Решение: 1)$$ 3 cos^{2} \alpha - 5 + 3 sin^{2} \alpha = 3(1 - sin^{2} \alpha ) - 5 + 3 sin^{2} \alpha = \\ 3 - 3 sin^{2} \alpha - 5 + 3 sin^{2} \alpha = 3 - 5 = -2 $$
    2) Согласно геометрическому смыслу производной, если в точку x0 проведена касательная к графику функции, то значение производной функции в точке касания x0 равно угловому коэффициенту этой касательной. Угловой коэффициент касательной, в свою очередь равен тангенсу угла наклона касательной. Отсюда сначала найдём тангенс угла наклона. Для этого найдём две целые точки, через которые проходит касательная(точки с целыми абсциссами). Первая точка (-2;0), вторая - (0;6) Построим соединим эти точки взаимно линиями, построив прямоугольный треугольник. И найдём тангенс тангенс угла наклона(этот угол между касательной и положителньым направлением оси OX). Длины обоих катетов соответственно 2 и 6. Тангенс угла прямоугольного треугольника равен отношению противолежащего катета к прилежащему. Так что tg a= 6/2 = 3.
    Согласно геометрическому смыслу это и есть значение производной в точке x0.

  • 1. Найдите угловой коэффициент касательной, проведенной к графику производной f ’(x) функции f(x)=3cos^2x в точке с абсциссой x0=пи/4
    2. Найдите тангенс угла наклона касательной, проведенной к графику функции f(x)=5x^2-7x+2 в точке с абсциссой x0=2


    Решение: Ответ производной три косинус квадрат икс ровно минус три синус два икс значение производной в точке пи /читворти  ровно минус три и это будет ответ первого задание

    Касательная-это та же прямая, функция которой задается f(x)=kx+b
    угловой коэффициент(k) =f’(x)=tg a ⇒
    f(x)=3cos²x
    f’(x)=-3sinx*2cosx=-6sinx*cosx=-3sin2x
    f’(x)=-3sin2x -это функция того графика к которой проведена касательная, значит, чтобы найти коэффициент касательной к графику нужно найти производную уже от функции f’(x)=-3sin2x
    ( f’(x) )’=(-3sin2x)’=-3cos2x*2=-6cos2x=-6cos(2*π/4)=-6cos(π/2)=0
    отв:k=0
    2)f(x)=5x²-7x+2
    f’(x)=10x-7=10*2-7=13
    f’(x)=tg a=13
    отв:13

<< < 121314 15 16 > >>