производная »

график функции производной - страница 12

  • Нахождение производной сложной функции.
    1.) у=1/2х^4 - 1/х - 4√х;
    2.) у= ln9х × сos(8[+4);
    3.) Построить график функции.
    у=х^4 - 2х^2 -3.


    Решение: 1.) у=1/2х^4 - 1/х - 4√х
    y`=2x³+1/x²-2/√x
    2.) у= ln9х × сos(8x+4)
    y`=9/9x *cos(8x+4)-8sin(8x+4)*ln9x=1/x*cos(8x+4)-8sin(8x+4)*ln9x
    3) у=х^4 - 2х^2 -3=(x²-1)²-4
    Строим y=x^4
    x  -2  -1  0  1  2
    y  16 1  0  1  16
    Сдвигаем ось оу на 1 влево и ось ох на 4 вверх
    (если двигаем график, то на 1 вправо и на 4 вверх

  • На рисунке изображён график функции y = −x2 + bx + c и четыре прямые, одна из которых является графиком производной данной функции. Укажите в ответе номер этой прямой.


    Решение: На рисунке изображён график функции y = −x2 + bx + c и четыре прямые, одна из которых является графиком производной данной функции. Укажите в ответе номер этой прямой.
    Производная параболы
    y’ = (−x2 + bx + с)’ = -2x+ b
    Из рисунка видно что с угловым коэффициентом k = -2 всего две прямые 3 и 2.
    При этом в точке максимума параболы производная равна нулю.
    Данному условию удолетворяет только прямая по номером 3.
    Ответ: 3

  • На рисунке изображен график функции f (x) и касательная к этому графику в точке x0. Найдите значение производной этой функции в точке x0.


    Решение: Геометрический смысл производной: производная - это тангенс угла между касательно и осью x.

    Т. е. нужно найти тангенс угла между касательной и осью x.

    Тангенс - это отношение противолежащего катета к прилежащему.

    Ищем такие точки, чтобы длины отрезков были целыми. Отчетливо виден треугольник к катетами 3 и 6.

    3 - противолежащий

    6 - прилежащий

    $$ tg\alpha=\frac{3}{6}=0,5 $$

    Важно заметить ещё какой будет знак у производной. Тут тоже довольно все просто: смотрим куда наклонена касательная: если она как бы возрастает (как в данном примере), то знак положительный. Если она будто убывает, то отрицательный. Ну и тут у нас знак положительный.

    Ответ: 0,5.

  • Функция y=f(x) определена на промежутке (-4; 2). На рисунке изображен график ее производной. Определите абсциссу точки, в которой касательная к графику функции y=f(x) параллельна оси ОХ


    Решение: Касательная будет параллельна оси Х в точках экстремумов производной.
    Данная функция имеет только один максимум в точке Х = -1 F’(x)~1.75.
    ОТВЕТ Х= -1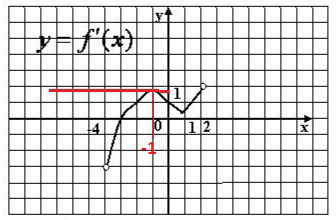

    Касательная будет параллельна оси Х в точках экстремумов производной.Данная функция имеет только один максимум в точке Х - F x . .ОТВЕТ Х -...

  • Функция y=f(x) определена на промежутке [-5;5]. На рисунке изображен график ее производной. Известно, что существует ровно одна касательная к графику функции, наклоненная под углом a к оси абсцисс. Найдите tga


    Решение: По условию, существует только одна касательная, наклонённая к графику функции под углом  α к оси абсцисс, значит на промежутке [-5;5] должна существовать одна касательная к графику производной функции.
    Ищем прямую у=а, имеющую только одну точку пересечения с графиком функции y=f(x)
    Только прямая у=4 имеет единственную точку пересечения. т. е. f’(x₀)=4.
    Следовательно, tgα = f’(x₀)=4

<< < 101112 13 14 > >>