производная »

график функции производной - страница 10

  • На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.


    Решение: Значение производной, вычисленное в точке касания = угловому коэффициенту касательной или тангенсу наклона касательной.
    угол α - угол между касательной и положительным направление оси Ох.
    прямоугольный треугольник:
    прилежащий к углу α катет =3
    противолежащий катет = 6
    tgα=6/3
    tgα=2
    f’(x₀)=2, f’(x₀)=2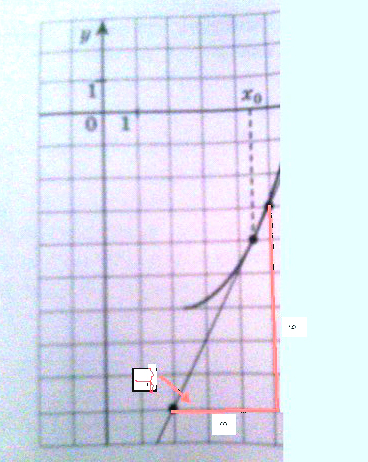

    Значение производной вычисленное в точке касания угловому коэффициенту касательной или тангенсу наклона касательной.угол  - угол между касательной и положительным направление...

  • На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой Xp
    Найдите значение производной функции x=y(x) в точке Xp


    Решение: Производная функции равна уравнению касательной в точке касания.
    По рисунку определяем это уравнение:
    у = (3/6) х + 4 = 0,5х + 4.
    По рисунку значение Хр = -3,5.
    Ответ: значение производной функции x=y(x) в точке
     Xp = -3,5 равно:
    f’(-3.5) = 0,5*(-3.5) + 4 = -1,75 + 4 = 2,25.

  • На рисунке изображен график функции y=f(x) и касательная к нему в точке с абсциссой х0. Найдите значение производной функции f(x) в точке x0.


    Решение: В таких заданиях специально отмечают еще 2 дополнительные точки на касательной. Нужны достроить прямоугольный треугольник (лучше снизу от касательной). При этом отрезок касательной, заключенный между этими точками, является гипотенузой. Получаем сторону=8 и =6.
    Производная=tg a, где а - угол между касательной и положительным направлением оси OX, в данном случае - с параллельной оси OX прямой, включающей в себя катет треугольника.
    tg a = противолеж. катет / прилеж. катет = 6 / 8 = 0,75

  • На рисунке изображены график функции y=f(x) и касательная к нему в точке абсциссой х0. Найдите значение производной функции f(x) в точке x0


    Решение: Воспользуемся геометрическим смыслом производной: это тангенс угла наклона касательной.
    тангенс угла наклона можно найти построив прямоугольный треугольник, гипотенуза которого - касательная.
    На вашем рисунке отмечены еще 2 "хорошие точки" (они выделены жирными черными точками). Эти точки можно использовать для построения треугольника.
    $$ tga=\frac{3}{6}=\frac 12 $$
    Ответ: 0,5

  • На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0


    Решение: Ищете на графике жирные точки, они совпадают с пересечением касательной с координатной сеткой. Находите расстояние между ними по вертикали, оно равно 6. Находите расстояние между ними по горизонтали, оно равно 8
    значение производной равно тангенсу угла наклона касательной
    f’(x0) = tg a = 6/8 = 0.75

    Значение производной в точке Х0 - это тангенс угла наклона касательной к оси ОХ,
    достроив прямоугольный треугольник по точкам (-5,1) (3,1) (3,7) видим, что тангенс угла наклона из этого треугольника  к оси ОХ (отношение противолежащей стороны к прилежащей)= 6/8 = 3/4
     

<< < 8910 11 12 > >>