производная »

график функции производной - страница 9

  • на рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0/


    Решение: Значением производной в какой-либо точке называют тангенс угла наклона касательной или ее угловой коэффицент. Т. к. касательная убывает, значит ее угловой коэффицент отрицательный, значит и тангенс отрицательный.

    Чтобы найти тангенс угла, нужно достроить его до прямоугольного треугольника.

    в данном случаенам нужно найти тангенс угла, выходящего из точки 2 на оси х.

    Достроим угол до треугольника с катетами 6 и 5.

    Тангенсом называется отношение противолежащего катета к прилежащему

    В данном случае это 6\5 т. е 1,2

    Не забываем что он отрицателен. Ответ -1,2

  • На рисунке изображены график функцииY=F(x) и касательная к нему в точке с абсциссой Xo. Найдите значение производной функции в точке Xo.


    Решение: Вам нужно найти f°(x₀), которое равно tgα

    f°(x₀)=tgα=5/4

    Прямая проходит через точки (7; 6) и (-1; -4)

    Найдем по ним уравнение прямой

    $$ \frac{x-7}{-1-7}=\frac{y-6}{-4-6} \\ \\ 48-8y=70-10x \\ \\ y=1,25x-2,75 $$

    Значение производной в точке касания равно угловому коефициенту касательной

    $$ f’(x_0)=k=1,25 $$

    Ответ: 1,25

  • На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой х0. Найдите значение производной функции f(x) в точке х0.


    Решение: F’(xo)=tga=2/8=1/4=0,25
    ***Пользуемся координатами точек, отмеченных на касательной (-4;5) и (4;3)
        Строим прямоугольный треугольник с вершинами в этих точках и в точке с координатами (-4;3). Далее, катеты этого треугольника равны 2 и 8.
    Теперь осталось найти тангенс угла наклона касательной к оси Ох.

  • На рисунке изображены график функции y=f(x) и касательная к нему в точке абсциссой x0. Найдите значение производной функции f(x) в точке x0.


    Решение: Геометрический смысл производной в точке:
    f’(x₀)=k(касат)=tgα
    см. рисунок
    Все углы, которые образуют касательные на рисунках с положительным направление оси ох - тупые.
    Из прямоугольных треугольников находим тангенсы смежных ( острых улов)
    3) tg(180°-α)=3,5/3,5=1
    180°-α=45°
    α=135°
    4)tg(180°-α)=2,2/8,5=22/85
    180°-α=arctg (22/85)
    α=180° - arctg (22/85)
    5)tg(180°-α)=3/1,5=2
    180°-α=arctg (2)
    α=180° - arctg (2)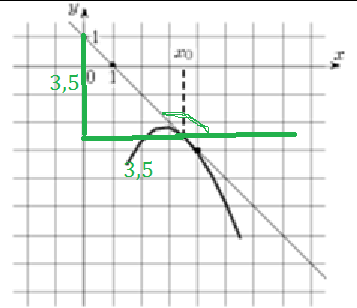

    Геометрический смысл производной в точке f x k касат tg см. рисунок Все углы которые образуют касательные на рисунках с положительным направление оси ох - тупые.Из прямоуголь...

  • На рисунке изображены график функции y=f(x) и касательная к нему в точке абсциссой x0. Найдите значение производной функции f(x) в точке x0.


    Решение: Геометрический смысл производной в точке:
    f`(x₀)=k(касат)=tgα
    1)  tgα=2,5/1,5 =5/3  (отношение противолежащего катета к гипотенузе)
    см. рисунок, провели прямую параллельную оси ох через точку касания и построили прямоугольный треугольник.
    2) tgα=2,25/4,5 =1/2

<< < 789 10 11 > >>