какое из данных чисел является рациональным
Два автомобиля выезжают одновременно из одного города в другой. Скорость первого на 20 км/ч больше скорости второго, и поэтому первый автомобиль приезжает на место на 2ч. 24мин. раньше второго. С какой скоростью шел первый автомобиль, если известно, что расстояние между городами равно 420 км?
Решение: Смотри вложение,там таблица
420/(x+20)+2.4=420/x
2,4+48×-8400=0
D=√82944=288
x=(-48+288)/4,8=50
50-скорость второго автомобиля, тогда
x+20=50+20=70 - скорость первого автомобиля
Ответ: 70 км/ч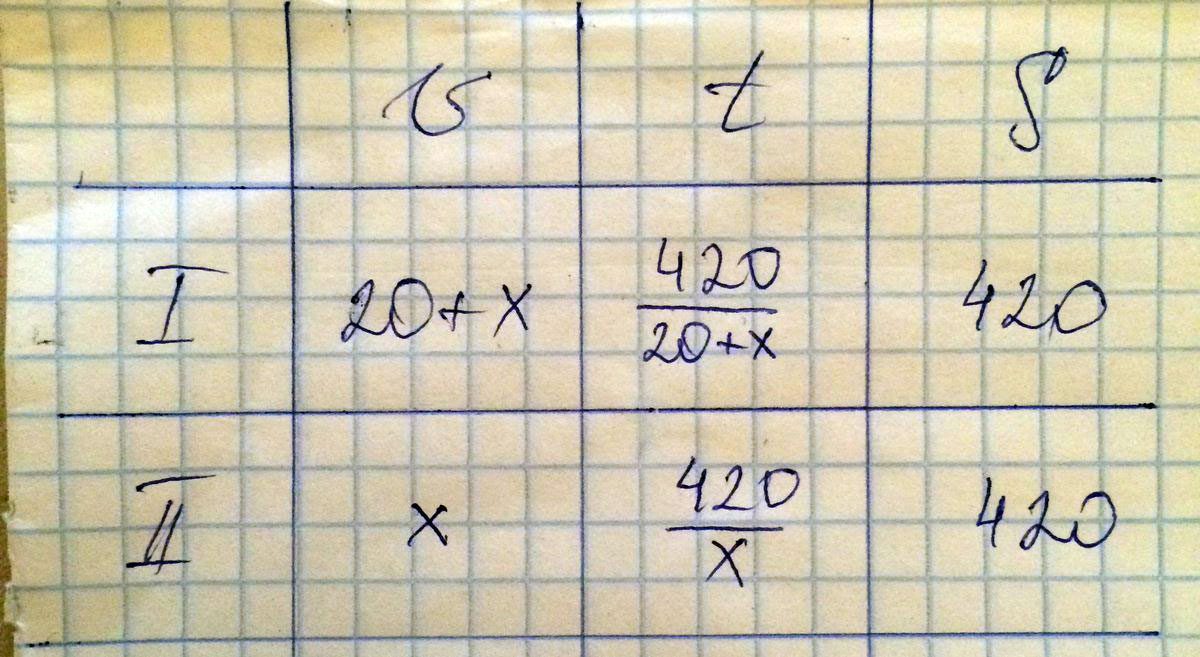
Из Цветочного города в Солнечный город одновременно выехали Незнайка на велосипеде и Винтик на мотоцикле. В тот же момент из Солнечного города им навстречу выехали Тюбик на велосипеде и Шпунтик на мотоцикле. Винтик едет в два раза быстрее Незнайки, а Шпунтик – в три раза быстрее Тюбика. Винтик встретил Тюбика в тот момент, когда Шпунтик встретил Незнайку. Чья встреча произошла ближе к Цветочному городу: Винтика со Шпунтиком или Тюбика с Незнайкой? Или как 10 возвести в 2012 степень?
Решение: Ближе к Цветочному городу произошла встреча Винтика со Шпунтиком, т.к. Шпунтик – в три
раза быстрее Тюбика, а Винтик едет в два раза быстрее Незнайки, Шпунтик быстрее приблизится к Цветочному городу, чем Винтик уедет от негоЧтобы возвести 10 в 2012 степень надо 10 * 10 * 10 * и так 2012 раз
Чтобы возвести нужное число в степень, то есть 10 нужно это число умножить само на себя столько раз во сколько нужно возвести то есть 10 нужно умножить само на себя 2012 раз
Результатом измерения является последняя цифра натуральной степени двойки (числа два в энной степени)
а) Выпишите общий ряд данных этого измерения
б) выпишите ряд данных этого измерения для n=2,3,5,7,8,10,11
в) выпишите ряд данных этого измерения для n=12,13,15,17,18,20,21
г) какова кратность варианты 8 среди всех результатов, полученных в заданиях б) и в)?
Решение:А)
ряд имеет вид
а={2;4;8;6;2;4;8;6;........;2;4;8;6;.......}
общий ряд данных 2;4;8;6
а1=2
а2=4
а3=8
а4=6
а(i+4)=а(i)
б)
n=2,3,5,7,8,10,11
2^2=4
2^3=8
2^5=32=10*3+2=?+2
2^8=128=10*12+8=?+8
2^10=2^8*4=(?+8)*4=?+32=?+2
2^11=2^10*2=(?+2)*2=?+4
аn={4;8;2;8;2;4}
в)
n=12,13,15,17,18,20,21
а(12)=а(4)=6
а(13)=а(1)=2
а(15)=а(3)=8
а(17)=а(1)=2
а(18)=а(2)=4
а(20)=а(4)=6
а(21)=а(1)=2
аn={6;2;8;2;4;6;2}
г)
кратность варианты 8 в примере б) равна 2
кратность варианты 8 в примере в) равна 1Каким образом можно возвести число в дробную степень. При решении задачи получился ответ : 243^3/5 ( 243 в степени 3/5 ).
Как поэтапно произвести данное действие?
Решение:Чтобы возвести число в дробную степень, нужно возвести в степень числителя и извлечь корень степени знаменателя.
В данном случае (для простоты)я бы представила 243 как 3⁵
Тогда
243^3/5 = (3⁵)^3/5
При возведение в степень показатель умножаются.
5 * 3/5 = 3
Следовательно
243^3/5 = (3⁵)^3/5 = 3³ = 27
Арифметическая прогрессия (аn) задана формулой аn=5n-7. Какое из следующих чисел является членом этой прогрессии?
А)56
Б)65
В)22
Г)43
Решение: Допустим аn=56
1)5n-7=56
5n=56+7
5n=63/5
n=12.6 (получилось не целое число, значит, не является)
2) допустим аn=65
5n-7=65
5n=65+7
5n=72/5(получится не целое число)
3) допустим an=22
5n-7=22
5n=22+7
5n=29/5(получится не целое число)
4) допустим an=43
5n-7=43
5n=43+7
5n=50/5
n=19(получилось целое число)
Ответ: Г) 43

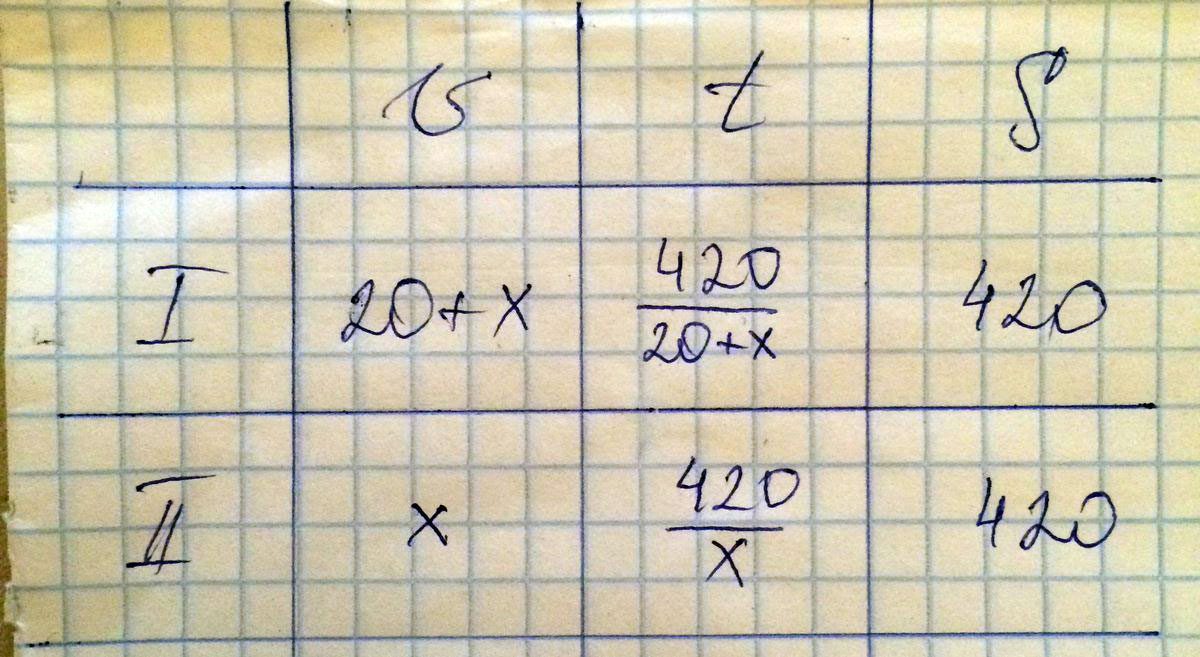
 Если ограничиваться только вещественными числами, то, как известно, действие извлечения корня не всегда выполнимо; корень четной степени из отрицательного числа не имеет ответа в области вещественных чисел. В связи с этим уже квадратное уравнение с вещественными коэффициентами не всегда имеет вещественные корни.Это обстоятельство приводит, естественно к расширению понятия о числе, к введению новых чисел более общей природы, частным случаем...
Если ограничиваться только вещественными числами, то, как известно, действие извлечения корня не всегда выполнимо; корень четной степени из отрицательного числа не имеет ответа в области вещественных чисел. В связи с этим уже квадратное уравнение с вещественными коэффициентами не всегда имеет вещественные корни.Это обстоятельство приводит, естественно к расширению понятия о числе, к введению новых чисел более общей природы, частным случаем...