график функции »

график степенной функции

  • На примере неравенств 3x^2 (в квадрате) +5x-2<0 и x^2 (в квадрате) +2x+6>0 покажите, как можно решить неравенство второй степени, используя свойства графика квадратичной функции.


    Решение:   3x^2+5x-2<0 приравниваем квадратный трехчлен 0 и ищем корни 
      3x^2+5x-2=0 D=25-4*3*(-2)=49 vD=7 x1=1/3 x2=-2 
      чертим ось х ,отмечаем на ней найденные значения х ,квадратный трехчлен имеет график -параболу ,оси вверх(а=3) ,парабола пересекает ох в точках х=1/ 3 и х=-2 ,дно параболы находится в отрицательной области у ,поэтому твоё неравенство будет отриц. (-2 , 1/3)
     x^2+2x+6>0 D=4-4*6*1=4-24=-20<0 ес
      ли дискриминант <0 то парабола не имеет точек пересечения с осью х и она расположена выше оси х ,а ,значит она положительна при всех х от( -бескон. до + бескон.)

  • В одной системе координат построить графики зависимости функций у=х в третей степени и у=корень третей степени из х. Как расположены относительно прямой у=х графики этих зависимостей?


    Решение: 2 картинки, просто масштаб разный. На втором графике значение аргумента и функций слева от графика. Степенные функции лежат по разные стороны относительно линейной функции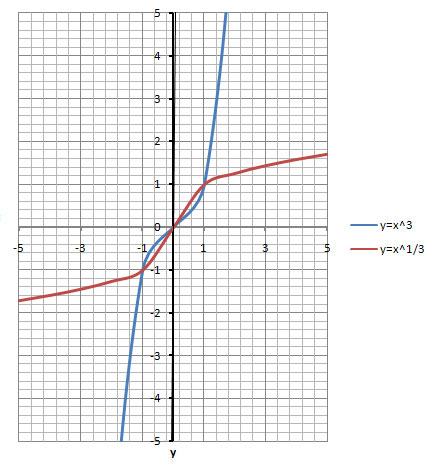 картинки просто масштаб разный. На втором графике значение аргумента и функций слева от графика. Степенные функции лежат по разные стороны относительно линейной функции...

  • 1) На примере неравенств 3х2+5х-2<0 и х2+2х+6>0 расскажите,как можно решить неравенство второй степени,используя свойства графика квадратичной функции.
    2) На примере неравенства (х-5)(х+7)(х+9)<0 расскажите, как решают неравенства методом интервалов


    Решение: 1) Нужно вычислить корни трехчлена, показать их на оси ох,нарисовать эскиз графика, учитывая направление ветвей параболы. Расставить знаки и выбрать нужные промежутки ( если > то +, если   < - то -). Смотри файл. Нужно вычислить корни трехчлена показать их на оси ох нарисовать эскиз графика учитывая направление ветвей параболы. Расставить знаки и выбрать нужные промежутки если то есл...

  • На примере неравенств 3x^2 (в квадрате) +5x-2<0 и x^2 (в квадрате) +2x+6>0 покажите, как можно решить неравенство второй степени, используя свойства графика квадратичной функции.


    Решение:   3x^2+5x-2<0 приравниваем квадратный трехчлен 0 и ищем корни 
      3x^2+5x-2=0 D=25-4*3*(-2)=49 vD=7 x1=1/3 x2=-2 
      чертим ось х, отмечаем на ней найденные значения х, квадратный трехчлен имеет график -параболу, оси вверх(а=3), парабола пересекает ох в точках х=1/ 3 и х=-2 ,дно параболы находится в отрицательной области у ,поэтому твоё неравенство будет отриц. (-2, 1/3)
     x^2+2x+6>0 D=4-4*6*1=4-24=-20<0 ес
      ли дискриминант <0 то парабола не имеет точек пересечения с осью х и она расположена выше оси х ,а ,значит она положительна при всех х от( -бескон. до + бескон.)

  • Постройте график функции у=х (в степени 7/4) + 1 и опишите ее свойства


    Решение: Область определения от 1 до бесконечности(1 включительно)
    Функция не является ни четной ни нечетной(общего вида)
    Функция не периодична
    Возрастает на промежутке от 1 до бесконечности(1 включительно)

    Минимальное значение функций 1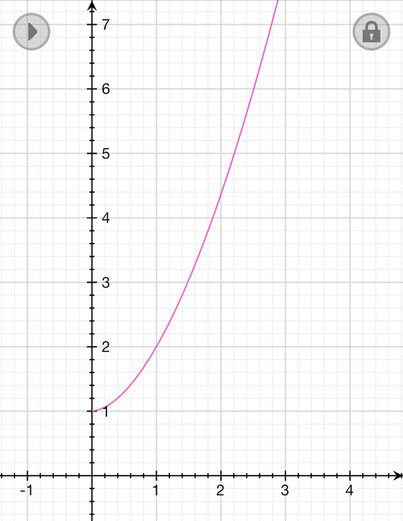
    Область определения от до бесконечности включительно Функция не является ни четной ни нечетной общего вида Функция не периодичнаВозрастает на промежутке от до бесконечности вк...
1 2 3 > >>