график функции »

график степенной функции - страница 3

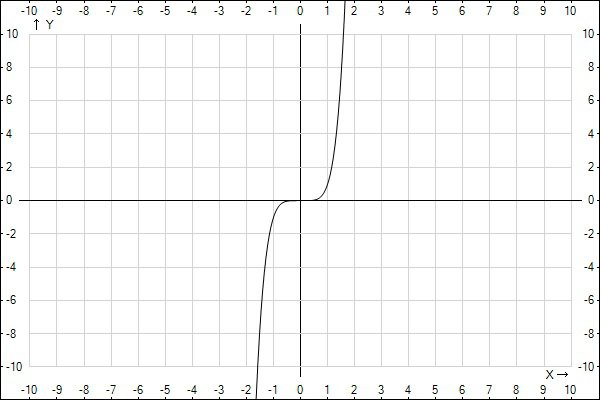
  • Постройте график функции y=x в 5 степени является ли функция четной или нечетной?


    Решение: фунция нечетная...............................................................................

    $$ f(x)=x^5\\f(-x)=(-x)^5=-x^5\\-f(x)=-x^5\\-f(x)=f(-x) $$

    Значит функция нечетная

    фунция нечетная............................................................................... f x x f -x -x -x -f x -x -f x f -x Значит функция нечетная...

  • Постройте график функции y=2x+3-x во второй степени и определите по графику промежуток, на котором функция возрастает


    Решение: Найдем вершину параболы
    $$ m=- \frac{b}{2a} = \frac{-2}{-2} =1 $$ - абсцисса
    $$ y=2\cdot 1+3-1=4 $$
    (1;4) - вершина параболы
    Ветви направлены вниз

    На рисунку видим что график возрастает на промежутке $$ (-\infty;4) $$, а убывает $$ (4;+\infty) $$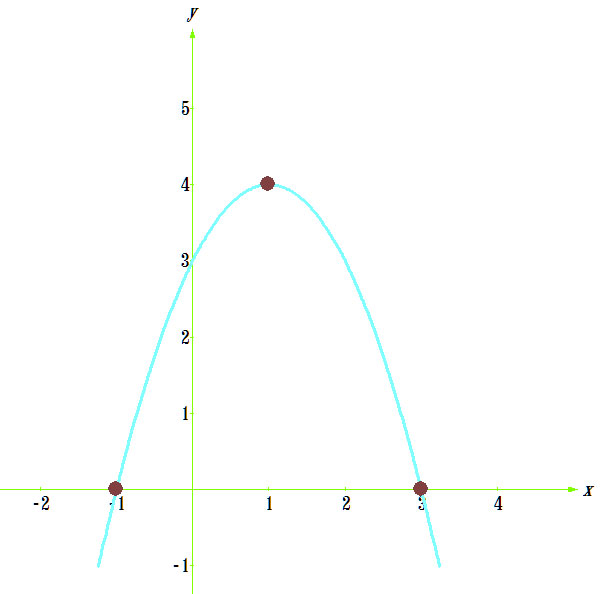 Найдем вершину параболы m - frac b a frac - - - абсцисса y cdot - - вершина параболыВетви направлены внизНа рисунку видим что график возрастает на промежутке  - infty а убывае...

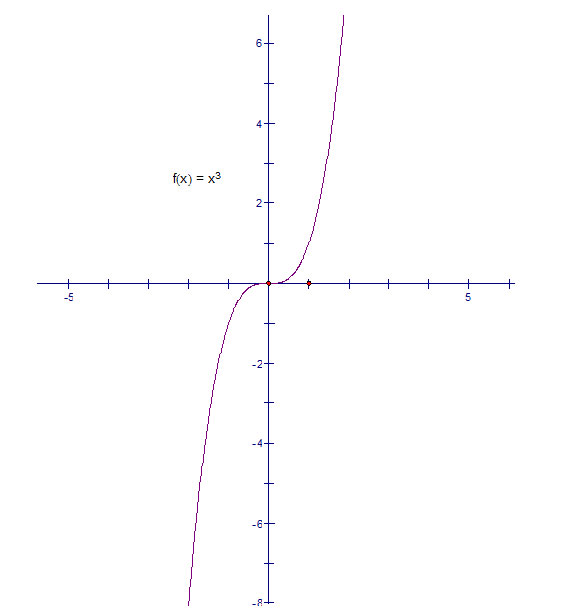
  • График какой функции получится если y=x в 3 степени


    Решение: У=х³, график кубическая парабола. ветви расположены в 1 и 3 четверти(координатных углах.
    график во вложении

    Кубическая параболла У х график кубическая парабола. ветви расположены в и четверти координатных углах.график во вложении Кубическая параболла...

  • 1 Найдите координаты вершин парабол у=3х(в степени 2),у=-5х(в степени 2) и y=x(в степени 2)2) для нахождения площади многоугольника используют его:

    3) точки графика нечетной функции симметричны относительно
    4) что является осью симметрии графика у=х(в степени 2)

    5) одна из сторон прямоугольника равна А ,а площадь S.как можно найти вторую его сторону?


    Решение: 1)у=3х²; у=-5х²; у=х² Все эти параболы имеют вершину в начале координат,значит координаты вершины (0;0)
    2)для нахождения площади многоугольника используют формулы
    3) Точки графика нечетной функции симметричны относительно начала координат, то есть точки с координатами (0;0)
    4)Ось симметрии параболы у=х² -это ось ординат ОУ : или прямая х=0
    5)чтобы найти другую сторону надо S:A

  • графиком какой из указанных функций является гипербола y=x/4 y=-x/4 y=4/x y=x во второйстепени


    Решение:

    y=4/x, так как простейшее уравнение гиперболы y=1/x, y=x в квадрате-это парабола, а 2 остальные-это прямые, только 1 возрастает, а другая убывает.

     y=4/х потому что уравнение функцией которого является парабола это y=k/х.

    все остальные это прямые и парабола.( y= x²)

<< < 123 4 > >>