график функции пересекает

В какой точке график функции у=х-2 пересекает ось координат А)(0,-2)
Б)(0,2)
В)(2,0)
Г)(-2,0)

Постройте в системе координат хОу график линейной функции у=ах+а², если известно, что он проходит через точку (1;2) и пересекает ось х левее начала координат. Чему равно значение а?

2=а+а²
а²+а-2=0
Д=1+8=9
а(1)=(-1+3)/2=1
а(2)=(-1-3)/2=-2
у=х+1 - пересек ось х левее нач координат в точке (-1;0); или у=-2х+4

Строим прямую у=х+1
точки в таблице:
х= 0 -2
у= 1 -1

Подставим значения координат заданной точки в уравнение прямой у=ах+а²:
2 = а*1 + а².
Получаем квадратное уравнение:
а² + а -2 = 0.
Квадратное уравнение, решаем относительно a: 
Ищем дискриминант:D=1^2-4*1*(-2)=1-4*(-2)=1-(-4*2)=1-(-8)=1+8=9;
Дискриминант больше 0, уравнение имеет 2 корня:a₁=(√9-1)/(2*1)=(3-1)/2=2/2=1;a₂=(-√9-1)/(2*1)=(-3-1)/2=-4/2=-2.

Значение а = -2 отбрасываем, так как прямая будет проходить сверху слева вниз направо и пересечёт ось х справа от 0.

Ответ: а = 1.

1. Решите систему уравнений:
\( \left \{ {{4x+y=2} \atop {6x-y=8}} \right. \)
2. Найдите координаты точки пересечения прямых 4x+3y-5=0 и -2x+y+5=0
3. Решите систему уравнений:
\( \left \{ {{y=x-1} \atop { x^{2}-2y=26 }} \right. \)
4. Решите систему уравнений:
\( \left \{ {{ x^{2}+ y^{2}=2 } \atop {xy=1}} \right. \)
5. Линейные функции заданы формулами:
А) y=-10x+3? Б) y=15-10x, В) y=5x
Графики каких функций пересекаются в точке:\( ( \frac{1}{5};1) \)
6. Решите систему уравнений:
$$ \left \{ {{5x+3y+ \frac{4}{7x-y}=5} \atop {5x+3y- \frac{4}{7x-y}=3 }} \right. $$
7. Решите систему:
$$ \left \{ {{y=2x-4} \atop {y=-x-1}} \right. $$

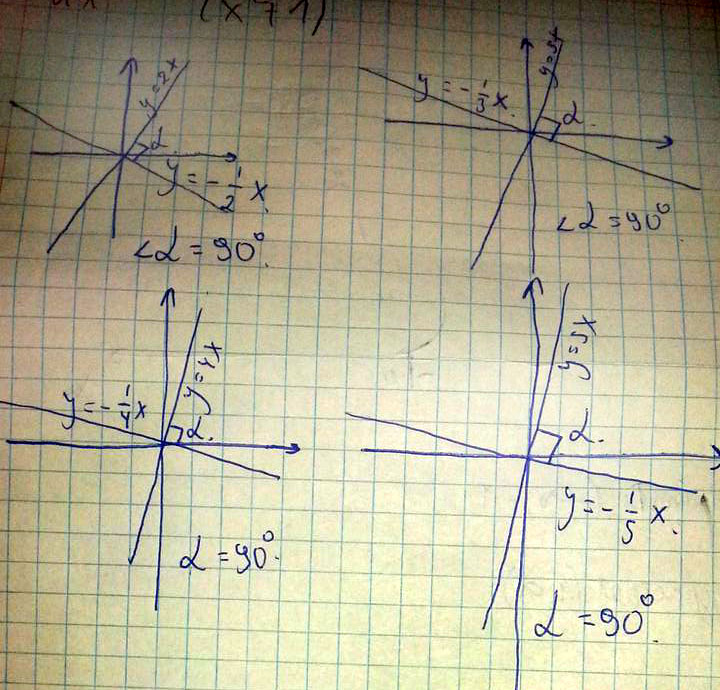
В одной системе координат постройте график функции: A) y=2x и у=-1/2х
б) у=-3х и у= 1/3х
В)у=4х и у=-1/4х
г)у=-5х и у=1/5х
определите угол между пересекающими прямыми.

1.Упростите выражение :
a) 2b*(3a+b)-(a-b)^2=?;
b)((2^2)^5 * 8) / 2^12=&?
(решение к обоим)
^x степень числа
*- знак умножения


2.Решите уравнение:

a) 6*(2-5x)=9-7*(4x-3) x=? Решение


3) Решите сист.уравнений 8x+y= -6
-2x+5y=12

4) Разложите на множители: b^3-81b=? (b в 3 степени)


5)Пересекаются ли графики функций?


а) y= -2x+3 и y = -2x+7 (найдите точку пересечения)

б) y= 3x-8 и y=2x+8 (найдите точку пересечения)^ - степень числа(цифры)*- знак умножения

 8х+у=-6
-8х+20у=48
  21у=42
у=42:21
у=2 

2b*(3a+b)-(a-b)^2=6ab+2b^2-(a^2-2ab+b^2)=6ab+2b^2-a^2+2ab-b^2=8ab-a^2=a(8b-a)

((2^2)^5*8)/2^12=2^10*2^3/2^12=2^13/2^12=2

6*(2-5x)=9-7*(4x-3);

12-30x=8x-6;

12-30x-8x+6=0;

18-38x=0;

18=38x;

X=18/38,x=9/19-дробь

8x+y=-6;

-2x+5y=12; => 8x+y=-6; -8x+20y=48; =>21y=42,y=2; 8x+2=-6,8x=-8,x=-1. (-1;2)

B^3-81b=b^2(b-81), ...