найдите координату точек пересечения графика функции - страница 27
Точка а имеет координату равную минус 4 а точка B координата равна 18 найдите координаты точек которые делят отрезок на 4 равные части
Решение: A(-4) B(18)
Пусть отрезок АВ разделен на 4 части точками С, D и Е
A________C_______D_______E_______B
Найдём их координаты:
1)18-(-4)=18+4=22 - расстояние АВ
2)22:4=5,5 - длина 1/4 расстояния АВ
3) -4+5,5=1,5 - координата точки С
4) 1,5+5,5=7 - координата точки D
5) 7+5,5=12,5 - координата точки Е
Ответ: C(1,5); D(7); E(12,5)
Длина отрезка |-4|+|18|=|22|. Длина половины равна 22/2=11, Четверти 11/2=5,5. 18-5,5=12,5 - одна координата. 12,5-5,5=7- вторая координата. 7-5,5=1,5 - третья. Ответ: 1,5; 7; 12,5.
Даны точки А(а, b), В(-а,b), С(-а, 3b) где а не равно 0, b не равно 0. Найдите координаты точек пересечения сторон треугольника ABC с осями координат.
Решение: Уравнение прямой по двум заданным точкам:$$ \frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1} $$
где x1, x2, y1, y2 - координаты точек.
Запишем уравнение для стороны AB:
$$ \frac{x+a}{a+a}=\frac{y+b}{b+b}\Rightarrow\frac{x+a}{2a}=\frac{y+b}{2b}\Rightarrow 2bx+2ab=2ay+2ab\\ 2bx=2ay\\ y=\frac bax $$
При пересечении данной прямой с осями координат одна из координат равна 0. В данном случае, если x=0, то и y=0, т. к. a и b не равны 0. Значит, эты прямая проходит через начало координат (0, 0).
Уравнение для стороны BC:
$$ \frac{x+a}{-a+a}=\frac{y+b}{3b+b}\Rightarrow (x+a)\cdot4b=(y+b)\cdot0\\ 4b(x+a)=0\\ beq0\Rightarrow x+a=0\Rightarrow x=-a $$
Данная прямая не имеет пересечений с осью OY, ось OX она пересекает в точке (-a, 0).
Уравнение для стороны AC:
$$ \frac{x-a}{-a-a}=\frac{y-b}{3b-b}\Rightarrow\frac{x-a}{-2a}=\frac{y-b}{2b}\Rightarrow 2bx-2ab=-2ay+2ab\\ 2ay=2ab-2bx\\ y=-\frac bax+b\\ y=0\Rightarrow -\frac bax+b=0\\ \frac bax=b\\ x=a\\ x=0\Rightarrow y=b $$
Эта сторона пересекает ось OX в точке (0, a), ось OY в точке (b,0).
Даны точки A(3;-1) B(4;1) C(2;0) D(3;1)
1) Пусть BM=6*BD,AN=4*AC. Найдите координаты точек М и N
2) Определите угол между векторами СA и DB
Решение: Вычисляем координаты векторов, вычитая из координаты конечной точки координаты начальной. У равных векторов координаты приравниваем. Для вычисления угла применяем формулу косинуса угла через скалярное произведение.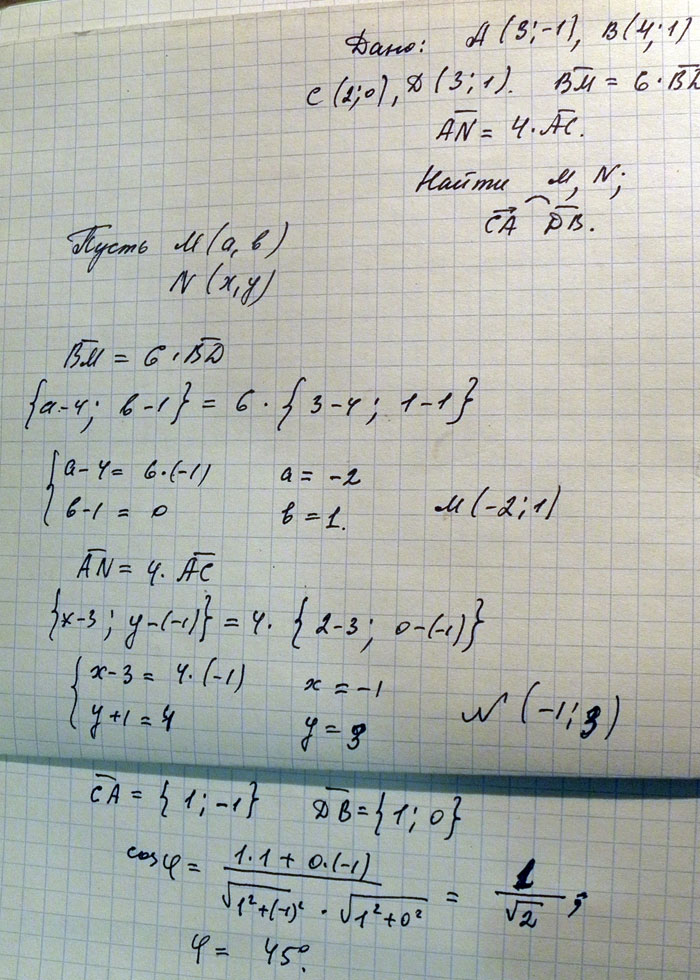
Найдите координаты точек пересечения с осями координат графиков данных уравнений A) 7x-2y=9 B) 25x+14y=24,5
Решение: 7x-2y=9
если х=0, то 7*0-2у=9
-2у =9
у= - 9/2 = -4,5
если у=0, то 7х - 2*0 =9
7х= 9
х=9/7 =1 целая 2/7
(0; -4,5) и ( 1 целая 2/7 ; 0)
25x+14y=24,5
если х=0, то 25*0+14у=24,5
14у=24,5
у=24,5/14
у= 1,75
если у=0, то 25х+14*0=24,5
25х= 24,5
х=24,5 / 25
х= 0,98
(0; 1,75) и (0,98; 0)1)
В треугольнике АВС MN – средняя линия, M ∈ AB, N ∈ ВС. О – точка пересечения медиан. М(0; 3), N(–2; 3), O(–1; 2).
а) Найдите координаты точек А и В.
б) Докажите, что точка К(0; 1) принадлежит медиане AN и делит ее в отношении 1:2.
2)
Докажите, что АВ диаметр окружности (x – 2)2 + (y – 1)2 = 10, если A(5; 2), B(–1; 0).
Решение: 1. а
Пусть А(х;0) (0- потому что А лежит на оси ОХ), В(х1; у1)
Т. к. М - середина ВА, то
(х1+х)/2=0, (0+у1)/2=3
Значит у1=6
Т. е. В(х1;6)
Рассмотрим СМ - медиана, и ОМ, лежащую на СМ
Т. к. СМ - мед. а О точка пересечения медиан, то ОМ=1/3СМ
Пусть С(х2;0) (0 т. к. С лежит на оси ОХ)
Вектор СМ имеет координаты{0-х2; 3-0}
{-х2;3}
ОМ{0-(-1);3-2}
ОМ{1;1}
ОМ*3=СМ
Так и с координатами
1*3=-х2
х2=-3
С(-3;0)
N-середина ВС
Значит (х1-3)/2=-2
х1=-1
В(-1;6)
(х+(-1))/2=0
х=1
А(1;0)

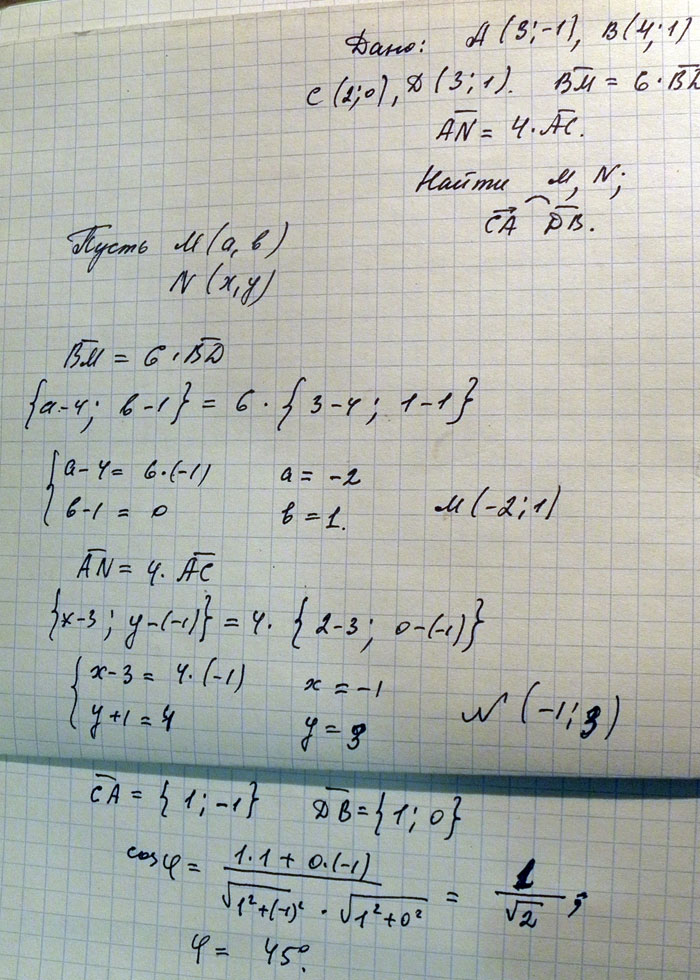
 Уравнение вида mx = n, к которому сводится любое линейное уравнение, может быть легко решено графически. На одном и том же рисунке построим графики двух функций: у = mx и у = n. Если эти графики пересекутся, то абсцисса точки пересечения и даст нам корень уравнения mx = n.
Если же эти графики не пересекутся, то это будет означать, что уравнение...
Уравнение вида mx = n, к которому сводится любое линейное уравнение, может быть легко решено графически. На одном и том же рисунке построим графики двух функций: у = mx и у = n. Если эти графики пересекутся, то абсцисса точки пересечения и даст нам корень уравнения mx = n.
Если же эти графики не пересекутся, то это будет означать, что уравнение... Рассмотрим некоторые вопросы поведения функций вида
$$ y=\frac{ax+b}{cx+d} \;\;\;(1) $$
где а, b, с и d - заданные числа, причем с отлично от нуля. Такие функции называются дробно-линейными (обычно, говоря о функциях вида (1), предполагают, что ad - bc \(\neq\) 0. Это условие мы заменяем здесь более простым условием с \(\neq\) 0.).
Прежде всего отметим, что дробно-линейная функция (1) определена при всех...
Рассмотрим некоторые вопросы поведения функций вида
$$ y=\frac{ax+b}{cx+d} \;\;\;(1) $$
где а, b, с и d - заданные числа, причем с отлично от нуля. Такие функции называются дробно-линейными (обычно, говоря о функциях вида (1), предполагают, что ad - bc \(\neq\) 0. Это условие мы заменяем здесь более простым условием с \(\neq\) 0.).
Прежде всего отметим, что дробно-линейная функция (1) определена при всех...