график функции »

найти координаты точки пересечения графиков - страница 2

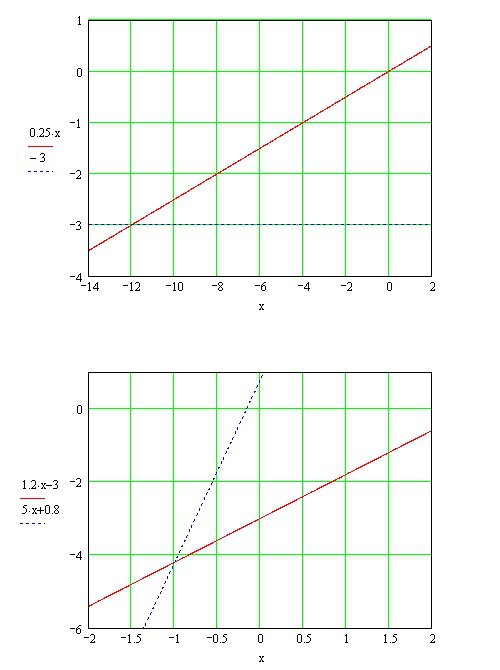
  • 1) Построить график функции в одной системе координат а)у=1/4х б) у+-3
    2) пересекаются ли графики f у=1,2х-3 и у=5х+0,8. Если графики фун. пересекаются, то найти точки их пересечения.


    Решение: 1) смотри вложение

    2) смотри вложение точка пересечения (-1; -4,2)

    ее найдем если приравняем 1,2х-3 = 5х+0,8 ==> -3-0,8 = 5x - 1,2x ==> -3,8 = 3,8x ==> x=-1

    смотри вложение  смотри вложение точка пересечения - - ее найдем если приравняем х-   х - - x - x - x x -...

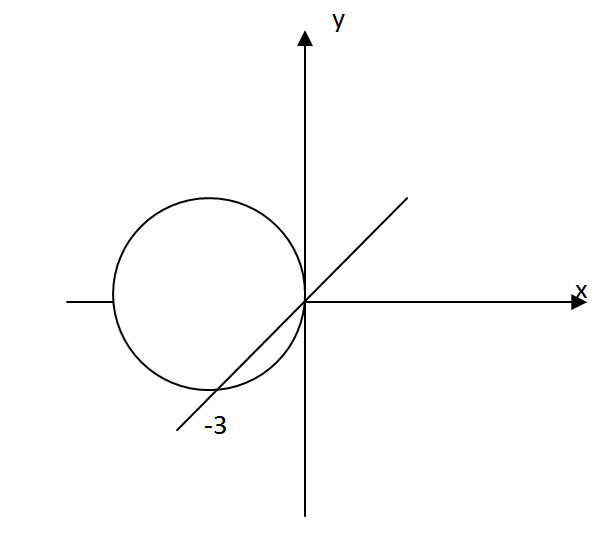
  • Постройте график уравнения (x^2+y^2+6y)*(x-y)=0 * это умножить
    ^ это степень


    Решение: 1)x²+y²+6y=0
    x²+(y+3)²-9=0⇒x²+(y+3)²=9
    окружность с центром (0;-3) и радиусом 3
    2)х-у=0⇒у=х
    биссектриса 1 и 3 координатных углов
    Решением будут все точки окружности и все точки прямой
    x y y x y - x y окружность с центром - и радиусом х-у у хбиссектриса и координатных угловРешением будут все точки окружности и все точки прямой...

  • Найдите значения b, при которых парабола y=2x^2 + bx + 18 касается оси Х. Для каждого значения b определите координаты точки касания


    Решение: парабола y=ax^2+bx+c касается оси Ох в вершине x=-b/(2a), y=c-b^2/(4a)=0

    поєтому

    x=-b/(2*2)=-b/4

    18-b^2/(4*2)=0

    18-b^2/8=0

    b^2/8=18

    b^2=18*8

    b^2=144

    b=12 или b=-12

    для b=12 : x=-12/4=-3

    для b=-12 :x=-(-12)/4=3

    овтет: при b=12 точка касания (-3;0)

    при b=-12 точка касания (3;0)

  • 1. Построить график функции, заданной формулой у= -1/3х + 2. Найдите по графику:
    а) у (- 3); у(6)
    б) значение х, при котором значение у(х) равно 1; 4.
    2. Не выполняя построения графика функции у = 60х - 29, выяснить, проходит ли он через точку: В (0,5; 1); С (0,3; 11).
    3. Построить график функции: у = -2,5х +3.
    4. Не выполняя построения графика функции, найти координаты точек пересечения его с осями координат, если у = - 0,8х + 1
    5. При каком значении b график функции у = 5х + b проходит через точку А (- 3; - 7)
    6. При каком значении k график функции у = kх - 3 проходит через точку М (- 5; 2).
    7. Найти координаты точки пересечения графиков функций у = 3х и у = -4х + 7
    8. Задать формулой линейную функцию, график которой проходит через точку М (- 6; 5) и параллелен графику функции у = - 2х + 7.


    Решение: 1) на графике красным цветом; а) x=-3; y=1+2=3; x=6; y=-2+2=0; б)y=1; 1/3x=2-y; x=6-3y; x=6-3=3; y=4; x=6-12=-6; 2) B)x=0,5 y=1; 1=60*0,5-29; 1=1; да; C) x=0,3; y=11; 11=60*0,3-29; 11=-11; нет; 3) на графике синим цветом; 4)y=0; -0;8x+1=0; 0,8x=1; x=1,25; x=0; y=1; (0;1) и (1,25;0); 5)x=-3; y=-7; -7=(-3)*5+b; -7=-15+b; b=8; 6) x=-5; y=2; 2=-5k-3; 5k=-5; k=-1; 7)3x=-4x+7; 7x=7; x=1; y=3*1=3; (1;3); 8)y=kx+b; k1=k2; k=-2; x=-6; y=5; 5=12+b; b=-7; y=-2x-7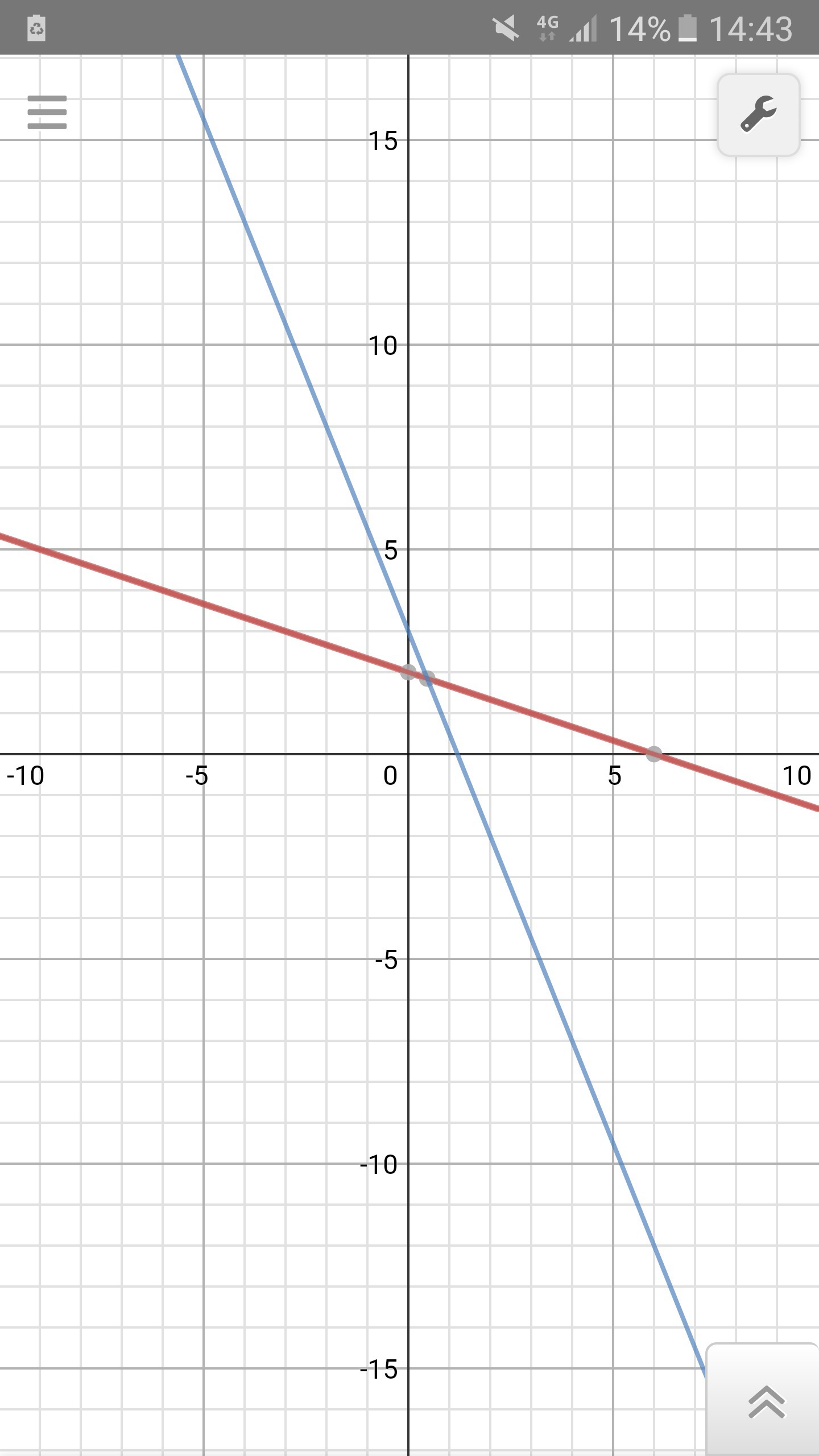

    на графике красным цветом а x - y x y - б y x -y x - y x - y x - - B x y - да C x y - - нет на графике синим цветом y - x x x x y и x - y - - - b - - b b x - y - k- k - k - x...

  • Найти координаты точки пересечения графика функций y=0,5x+1и y=-x+4


    Решение: $$ \left \{ {y=0.5x+1} \atop {y=-x+4} \right. \\ 0.5x+1=-x+4\\ 0.5x+x=4-1\\ 1.5x=3\\ x=2\\ y=-2+4=2 $$
    Ответ (2;2)

    Можно составить систему уравнений 
    у=0,5х+1
    у=-х+4
    так как в левой части мы в обоих уравнениях приравниваем к у, то можно приравнять правые части 
    0,5х+1=-х+4
    у=-х+4
    ________________
    0,5х+1=-х+4
    0,5х+х=4-1
    1,5х=3
    х=2
    ________________
    х=2
    у=-х+4
    х=2
    у=-2+4
    х=2
    у=2
    Ответ: (2;2)
    Проверка:
    2=0,5*2+1; 2=2
    2=-2+4; 2=2
    Решено верно
    Точки пересечения графиков функций: (2;2)

<< < 12 3 4 > >>