график функции »

найти координаты точки пересечения графиков - страница 4

  • 1. Определите координаты вершины параболы : y=x²-12x+33
    2. Найти точки пересечения параболы с осями координат : y=x²-10x+24
    3. Построить график функции : y=(x-2)²+1


    Решение: $$ 1.\;A\left(-\frac b{2a};\;-\frac{b^2-4ac}{4a}\right)\\-\frac{b}{2a}=\frac{12}2=6\\-\frac{b^2-4ac}{4a}=\frac{4ac-b^2}{4a}=\frac{132-144}{4}=-3\\A(6;\;-3)\\\\2.\;c\;OY,\;x=0\Rightarrow\;y=0\\B(0;\;0)\\c\;OX,\;y=0\Rightarrow x^2-12x+33=0\\D=144-4\cdot33=12\\x_{1,2}=\frac{12\pm\sqrt{12}}2\\x_1=6-\sqrt3,\;x_3=6+\sqrt3\\C(6-\sqrt2;\;0),\;D(6+\sqrt2;\;0)\\\\3.\;y=x^2-2x+5 $$
    График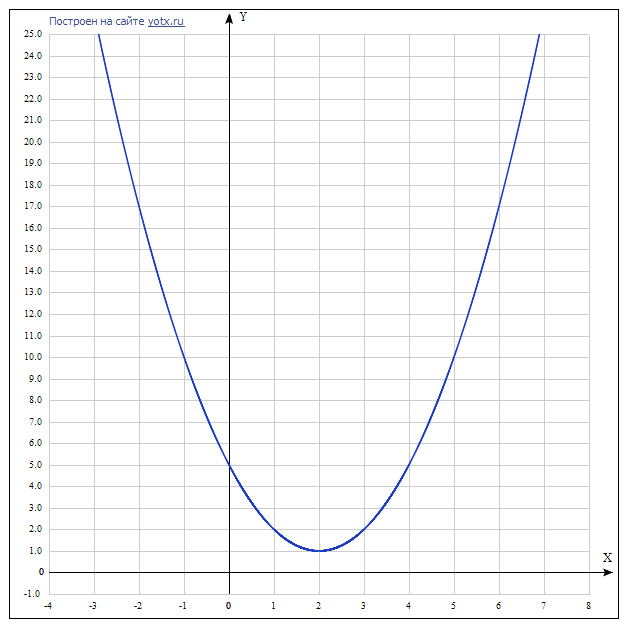

    . A left - frac b a - frac b - ac a right - frac b a frac - frac b - ac a frac ac-b a frac - - A - . c OY x Rightarrow y B c OX y Rightarrow x - x D - cdot x frac pm sqrt x -...

  • Найти точку пересечения функции с осями координат
    у=-2x^2+5x+6


    Решение:
    2x^2-5x-6=0
    D=25-4*2(-6)=√73
    X1=(5+√73)
      -
      4
    X2=(5-√73)
      -
      4
    Это пересечения с осью х.
    y=-2( 5+√73)^2+(5+√73)+24 -50-20√73-146+25+5√73+24 ( - 147-15√73)
      - = - = -
      4 4 4
     
    Аналогично решаем второе, но с +, получаем ( -147+15√73)
      -
     Это с y. 4
     
    Вроде как-то так. Смущают меня иррациональные числа, надеюсь, правильно

  • Найти точки пересечения с осями координат касательной, проведенной к графику функции
    \( y=4\sqrt{x} \) в точке М(1;4).


    Решение: Уравнение касательной yk = f (x0) +  f ’(x0) · (x − x0).
    f (x0) = 4*√1 = 4.
    f ’ (x) = 2/√x,
    f ’ (0) = 2/√1 = 2.
    yk = 4 +  2 · (x − 1).
    yk = 4 +  2x − 2 = 2x + 2.
    Теперь находим точки пересечения касательной с осями координат: yk = 2x + 2.
     у = 0 0 = 2х + 2 2х = -2 х = -1.
     х = 0  у = 2*0 + 2 = 0 + 2 = 2  у = 2.

  • Дана функция y=-x^2+4x+5
    а) Найти точки пересечения графика функции с осями координат.
    б) Не строя графика, найти наибольшее значение функции.


    Решение: Это парабола, ветви направлены вниз. Пересечение с осью ОУ точка (0;5), ось ОХ : решаем квадратное уравнение -х^2+4х+5=0 D=16+20=36 х1=-1, х2=5. значит ось ОХ пересекает в точках (-1;0) и (5;0). Находим производную: у’= -2x+4. Следующий шаг: критические точки: -2х+4=0.2х=-4, х=2. Подставляем значение 2 в функцию: у=-4+8+5=9. Наибольшее значение 9!

    1) точек пересечения с осью ох (-1;0) (5;0)
    с осью оу: (0;5)
    2)$$ x=- \frac{b}{2a} $$ ось симметрии, след х=2 точка максимума
      у=9 - максимум функции

  • Найти точки пересечения графика функции с осями координат: у=5х+2/3х-1


    Решение: если график данной функции пересекает ось ОХ в точке А, то она имеет координаты А(х;0), имеем уравнение:

    (5х+2)/(3х-1)=0,

    5х+2=0,

    х=-0,4, значит точка А имеет координаты (-0,4;0).

    Допусти что график данной функции пересекает ось ОУ в точке В, то она имеет координаты В(0; у), имеем второе уравнение:

    5*0+2/3*0-1=-2, значит точка В имеет координаты (0;-2).

    Ответ:(-0,4;0) и (0;-2).

<< < 234 5 6 > >>