график функции »

найти координаты точки пересечения графиков - страница 6

  • 1) Как из графика функции y=-2x можно получить график функции y=-2x-3 ? Нужно подробно написать 2) Построить график функции и найти точки пересечения его с осями координат - 1) y=4x+8 2) y=-3x+6 Все Можете решить нужно1


    Решение: 1) Сдвинуть на 3 единицы вниз
    2) y=4x+8
    Если х=0 то у=8
    Если у=0 то х=-2
    y=-3x+6
    Если х=0 то у=6
    Если у=0 то х=2

    1) нужно перенести прямю, отвечающую уравнению у=-2х, на три единицы вниз вдоль оси у, при этом не меняя ее наклон. Просто параллельный перенос.
    2) у=4х+8
      точка перес с Ох: х=0 > у=4*0 + 8 > y=8. т. о. точка с координатами (0;8)
      точка перес с Оу: у=0=4х+8 > x=-2 > т. о. точка с координатами (-2;0)
     y=-3х+6
    точка перес с Ох: х=0 > у=-3*0 + 6 > y=6. т. о. точка с координатами (0;6)
      точка перес с Оу: у=0=-3х+6 > x=2 > т. о. точка с координатами (2;0)

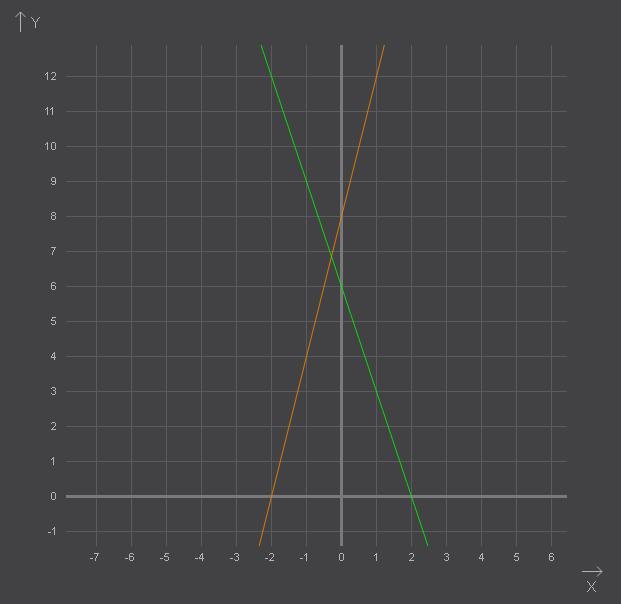
    Сдвинуть на единицы вниз y x Если х то у Если у то х - y - x Если х то у Если у то х нужно перенести прямю отвечающую уравнению у - х на три единицы вниз вдоль оси у при этом...

  • Найти точки пересечения графика функции y = 5x - 3 с осями координат


    Решение: Точка пересечения с осью х у=0, с осью у - х=0.
    0=5х-3
    х=3/5 с осью х (3/5;0)
    у=-3 с осью у (0; -3).

    Когда график пересекается с осями координат, то при пересечении с Ох его абсцисса = о, соответственно и при пересечении с Оу, ордината = о
     1) 5х -3=0 ⇒ х=5/3 = 0,6 ⇒ (0,6; 0) - с абсциссой
    2) y = -3, следовательно (0; -3) – точка пересечения с осью ординат;

  • Не выполняя построения найти точки пересечения графика функции y=0,2x+6 с осями координат


    Решение: Когда график пересекает ось абсцисс - в ноль превращается у, когда пересекает ось ординат в ноль превращается х.
    у=0 ⇒ 0,2х + 6 = 0            
             0,2х = -6
             х = -30
    х = 0 ⇒ у = 0,2 * 0 + 6
                у = 6
    Вот искомые точки х = -30
                                 у = 6

    В точке пересечения с осью у х=0:
    у=0,2*0+6=6
    Точка пересечения с осью у имеет координаты (0; 6).
    В точке пересечения с осью х у=0:
    0=0,2х+6
    0,2х=-6
    х=(-6):0,2
    х=-30
    Точка пересечения с осью х имеет координаты (-30; 0).

  • Исследовать функцию, построить график: y= -1/6*x³+2x; Работа делается по шагам
    1) Найти ОДЗ
    2) находим асимптоты графика функции
    3) четная симметрия графика или нет
    4) находим точки пересечения график с осями координат
    5) Находим интервалы монотонности и экстремумы
    6) Находим интервалы выпуклости вогнутости точки перегиба
    7) Строим график функции


    Решение: ДАНО
    Y= -1/6*x³+2x
    ИССЛЕДОВАНИЕ.
    1. Область определения - Х∈(-∞,+∞) - непрерывная, разрывов нет.
    2. Пересечение с осью Х.
    х1 = -2√3, х2 = 0, х3 = 2√3.
    3. Пересечение с осью У - У(0) = 0.
    4. Поведение на бесконечности.
    limY(-∞) = +∞
    limY(+∞) = -∞
    5. Исследование на четность.
    Y(-X) = - Y(X) - функция нечетная.
    6. Первая производная
    Y’ = - 1/2*x² + 2.
    Нули производной - х1= -2 х2= 2.
    7. Максимум - Y(2) = 2.6667
    Минимум - Y(-2) = - 2.6667.
    8. Монотонность.
    Убывает - Х∈(-∞,2]∪[2,+∞)
    возрастает - Х∈[-2,2].
    9. Вторая производная - точка перегиба
    Y" = -2x=0 при Х=0.
    10. Вогнутая - Х∈(-∞,0]
    Выпуклая - X∈[0,+∞)
    11/ График прилагается.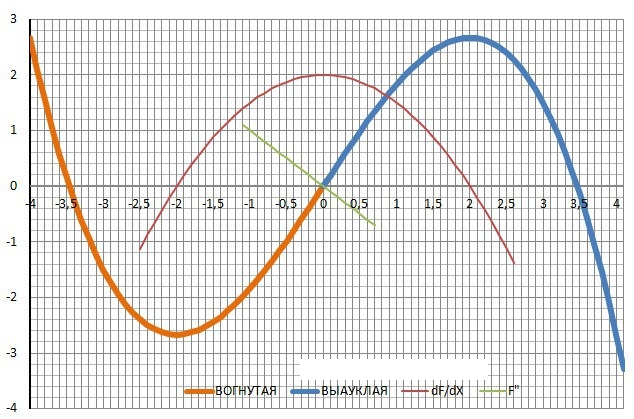 

    ДАНОY - x xИССЛЕДОВАНИЕ. . Область определения - Х - - непрерывная разрывов нет. . Пересечение с осью Х.х - х х . . Пересечение с осью У - У . . Поведение на бесконечности.li...

  • 1 Функция задана формулой y=2x+3 принадлежит ли графику функции точки A(1;5) B(-1;-1)?
    2Постройте график функции y=2x+6 Укажите точки пересечения графика с осями координат.
    б) укажите с помощью графика чему равно знание x=1,5
    4 найти точку пересечения графиков функций y=3 и y=2x-1
    5запишите уравнение прямой параллельной графику функции y=-7x -15 и проходящей через начало координат


    Решение: 1. у=2х+3 А(1;5): 5=2×1+3;5=5-принадлежит, т. к выполняется равенство. В(-1;-1): -1=2×(-1)+3;-1=1-не принадлежит, т. к равенство не выполняется.2. для построения графика задаем координаты х=0, у=6; х=-1, у=4(наносить их на плоскость и получаете прямую-это и будет график) а.) точки пересечения у тебя будут(-3;6); б.) у=2×1,5+6=9.3. у=kx. 4=-2k; k=-2, функция для построения графика это у=-2х,(задаем координаты для построения х=0, у=0; х=1, у=-2).4.3х=2х-1;3х-2х=-1; х=-1-это точка пересечения. у=-7х-15, уравнение параллельной прямой, проходящей через начало координат это у=-7х(прямые параллельны, когда коэффициенты при х равны, т. е k1=k2=-7)

    . у х А -принадлежит т. к выполняется равенство. В - - - - - -не принадлежит т. к равенство не выполняется. . для построения графика задаем координаты х у х - у наносить их н...
<< < 456 7 8 > >>