график функции »

найти координаты точки пересечения графиков - страница 5

  • Найти точки пересечения графика функции с осями координат
    y=1/6x^3+2x^2+6x


    Решение: Чтобы найти точки пересечения функции с осями нужно:
    с осью OY:
    подставить вместо х - нули:
    $$ y= \frac{1}{6}x^3+2x^2+6x\\\\ y(0)=\frac{1}{6}\cdot0^3+2\cdot 0^2+6\cdot0=0 $$
    Пересекает ось ОY в 0
    c осью ОХ:
    приравнять выражение к нулю и решить уравнение:
    $$ \frac{1}{6}x^3+2x^2+6x=0\\\\ \frac{1}{6}x^( x^2+12x+36)=0\\\\ \frac{1}{6}x(x+6)^2=0\\\\ \frac{1}{6}x=0\\\\ x=0\\\\ x+6=0 \\x=-6 $$
    На оси ОХ пересекает в -6 и 0

  • Найти точки пересечения графиков функций с осями координат y=-4x^2+8x-3


    Решение: Y=-4x²+8x-3
    1) Точки пересечения с осью Ох:
      -4х²+8х-3=0
      4х²-8х+3=0
      D=(-8)²-4*4*3=64-48=16=4²
      x₁=(8+4)/(2*4)=12/8=1,5
      x₂=(8-4)/(2*4)=4/8=0,5
      (1,5;0) и (0,5;0) - точки пересечения с осью Ох
    2) Точка пересечения с осью Оу:
      у(0)=-4*0²+8*0-3=-3
      (0;-3) - точка пересечения с осью Оу

  • А) y=x²-4x²-7x
    б) \( y= \frac{16}{ x^{2} ( x - 4 )} \)
    1) найти области допустимых значений
    2) проверить чётность - нечетность функции.
    3) найти точки пересечения с осями координат.
    4) найти асимптоту.
    5) найти первую производную, интервалы рост - падение функции, точки максимума - минимума.
    6) найти вторую производную. интервалы выпуклости - вогнутости и точки перегиба.
    7) построить график.
    .


    Решение: ДАНО
    Y = x³ - 4x² - 7x
    ИССЛЕДОВАНИЕ
    1. Область определения - Х∈(-∞,+∞) - все R.
    2. Пересечение с осью абсцисс - ось Х
    Х1 = 2 - √11 ~ 1.32 и Х2 = 0 и Х3 = √11+2 ~5.32 
    3. Пересечение с осью ординат - ось У - Х4 =0.
    4. Поведение на бесконечности.
    У(+∞) = +∞ и У(-∞) = -∞.
    5. Исследование на четность.
    У(х) = х³-4х²-7х
    У(-х) = - х³-4х²+7х
    Функция ни чётная ни нечетная.
    6. Производная функции - красная
    3х² - 8х -7.
    7. Корни производной - точки экстремума.
    х5 = 4/3 - √37/3 ~ - 0.69
    х6 = √37/3 - 4/3 ~ 3.36
    8. Максимум - Y(-0.69) = 2.6
    Минимум - Y(3.36) = - 30.75
    8. Возрастает - Х∈(-∞,0.69]∪[3.36,+∞)
    Убывает - Х∈[-0.36,3.36]
    9. Вторая производная
    Y" = 6x - 8 - зеленая прямая
    Точка перегиба - Х=4/3 = 1,33
    10. Выпуклая - Х∈(-∞,0] - оранж
    Вогнутая - X∈[0,+∞) - синия
    11. график прилагается.

  • Построить график функции у = - 3х + 6 и найти точки пересечения с осями координат.


    Решение: Ответ: (2;0), (0;6).

    Решение уравнения:
    Для начала нам нужно найти x,y
    Для этого мы подводим подобные слагаемые, возьмём например:(2,0), как мы знаем первое число это x, а второе y нам удобнее решать уравнение с маленькими слагаемыми, а следующая пара чисел, у нас будет(0;6)
    Строим координатную плоскость, поесть график. отмечаем наши точки и проводим прямую, вот и все, наш график готов!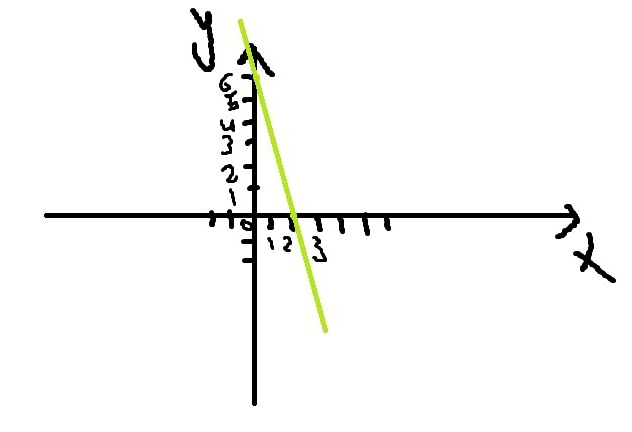

    Ответ . Решение уравнения Для начала нам нужно найти x yДля этого мы подводим подобные слагаемые возьм м например как мы знаем первое число это x а второе y нам удобнее решат...

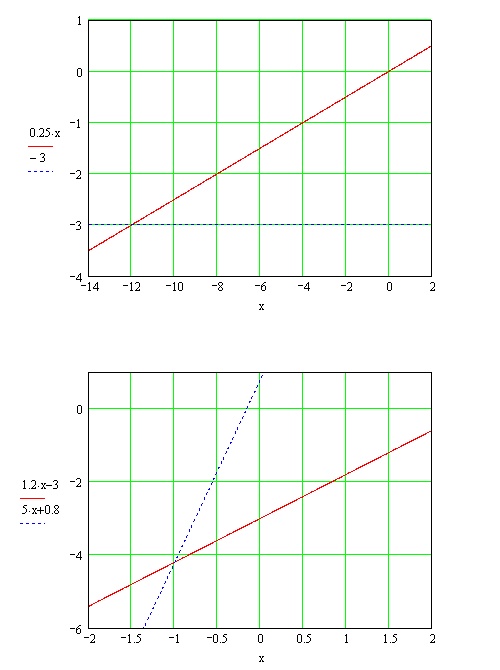
  • 1) построить график функции в одной системе координат а) у=1/4х б) у+-3 2) пересекаются ли графики f у=1,2х-3 и у=5х+0,8 если графики фун. пересекаются то найти точки их пересечения


    Решение: 1) смотри вложение

    2) смотри вложение точка пересечеия (-1; -4,2)

    ее найдем если приравняем 1,2х-3 = 5х+0,8 ==> -3-0,8 = 5x - 1,2x ==> -3,8 = 3,8x ==> x=-1

    смотри вложение  смотри вложение точка пересечеия - - ее найдем если приравняем х-   х gt - - x - x gt - x gt x -...
<< < 345 6 7 > >>