координаты »

найдите координаты точки - страница 2

  • Найдите координаты точки графика функции y=6x-5
    1) абсцисса и ордината которой равны между собой;,
    2) сумма координат которой равна 30


    Решение: Первую точку находим графически - А(1;1) - на чертеже. ОТВЕТ
    Вторую точку находим алгебраически
    Дано
    Y= 6x-5
    X+Y=30
    Подставили первое уравнение
    X + 6x-5 = 30
    7X=35
    X = 5 - абсцисса
    Y= 6x-5 = 30-5 = 25 - ордината
    Окончательно координаты точки = В(5:25) - ОТВЕТ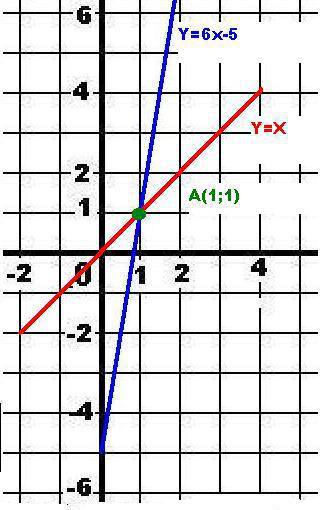

    Первую точку находим графически - А - на чертеже. ОТВЕТВторую точку находим алгебраическиДано Y x- X Y Подставили первое уравнениеX x- X X - абсциссаY x- - - ординатаОкончате...

  • Графики функции.
    Найдите координаты точки графика функции y=-3x+5, если эти координаты равны.


    Решение: Пусть точка A(x;y) - искомая точка.
    По условию, координаты равны между собой, значит: x=y
    Подставим в уравнение функции:
    y(x)=-3x+5=-3y+5
    y=-3y+5
    4y=5
    y=5/4=1.25
    x=1.25
    A(1.25;1.25)
    Ответ: x=y=1.25

    У=-3х+5
    по условию у=х
    х=-3х+5
    х+3х=5
    4х=5
    х=5/4=1,25⇒у=1,25
    Координаты точки (1,25;1,25)

  • Найдите координаты точки пересечечения графика функции y=10x^2-9x 2 с осью Ox.


    Решение: Приравниваем к 0
    получаем квадратное уравнение.
    D=81-80=1
    x1=2/5
    x2=1/2
    т. е. график пересекает ось х в двух точках (0;2/5) (0;1/2)

    Чтобы найти точки пересечения двух графиков, их нужно приравнять
    $$ y=10 x^{2} -9 x+2 \\ y=0 $$
    Приравниваем:
    $$ 10 x^{2} -9 x+2=0 $$
    Решаем с помощью дискриминанта:
    $$ D=81-80=1 \\ x_{1} = \frac{9+1}{20} = \frac{1}{2} \\ x_{2}= \frac{9-1}{20}= \frac{2}{5} $$
    Мы получили два корня, то есть две точки пересечения.
    $$ A( x_{1};y_{1})=A( \frac{1}{2};0) \\ B( x_{2};y_{2})=A( \frac{2}{5};0) $$

  • А) Найдите координаты точки пересечения графика линейной функции у = - 2х + 6 с осями координат. б) определите принадлежит ли графику данной функции точка М (15; -24)


    Решение: Надо 24-15:2 равно 3 все

    А)
    ОСЬ Ох(у=0)
    -2х+6=0
    6=2х
    3=х
    х=3
    И так точка пересечения графика заданной функции с осью Ох: (3;0)
    С Осью Оу(х=0)
    у=-2*0=6
    у=0+6
    у=6
    И так точка пересечения графика заданной функции с осью Оу: (0;6)
    б)
    Подставим вместо х и у координаті точки М и посмотрим віполняется ли равенство
    -24=-2*15+6
    -24=-30+6
    -24=-24
    Точка М(15;-24) принадлежит заданной функции

  • не выполняя построения, найдите координаты точки пересечения графика линейной функции: у=7х-1 и у=2х


    Решение: Составим систему уравнений:

    у=7х-1

    у=2х

    Подставляем 2х в первое уравнение. Получается следующее: 

    2х=7х-1

    у=2х

    Решаем первое уравнение

    2х=7х-1

    2х-7х=-1

    -5х=-1

    х=1/5

    Подставляем получившуюся координату во второе уравнение

    у=2х

    у=2*1/5=2/5

    Ответ: (1/5; 2/5)

<< < 12 3 4 > >>