координаты »
найдите координаты точки - страница 4
Постройте график функции у=2х-3. Найдите координаты точки пересечения этого графика с прямой у=-5х+11
Решение: у=2х-3 - лин. ф-ция, графиком явл. прямая проходящая через 1 и 3 угол, т. к. к=2>0.
Тоже самое и ко второй функции.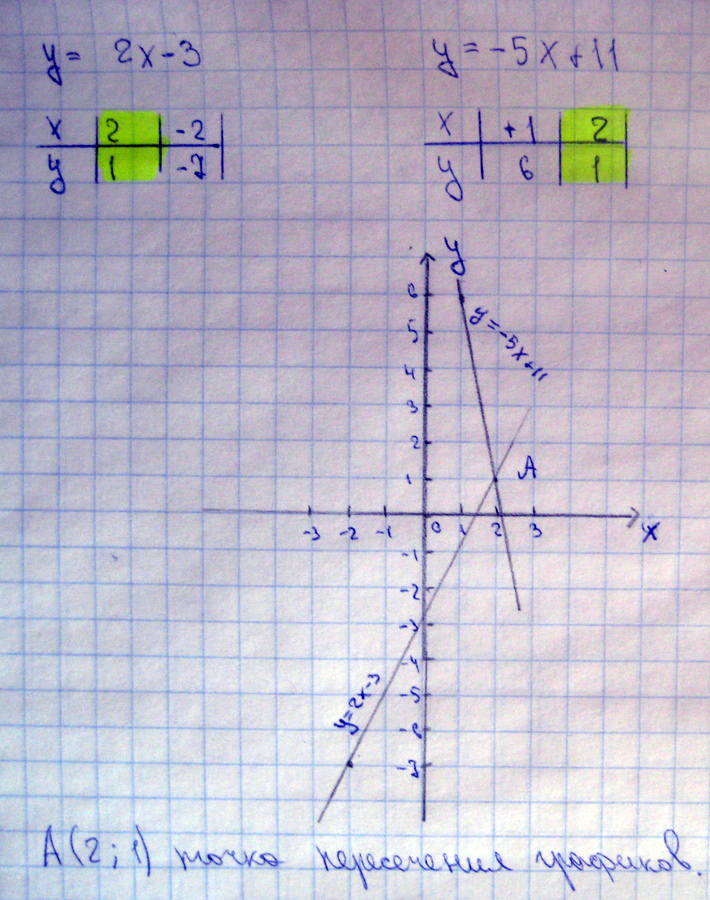
Постройте график функции у=2х-3 и найдите координаты точки пересечений этого графика с прямой у=-5х+11
Я нарисовал систему координат и отметил точки х=0 у=-3, х=2 у=1 (Как на скрине)
Что делать дальше?
Решение: Тебе нужно построить два графика :
у=2х -3 и у=-5х+11
Только точек нужно немного больше
Где графики пересекутся в одной точке - это и будет точка пересечения.
Проверить эти координаты можно с помощью решения системы двух уравнений.
См. приложение.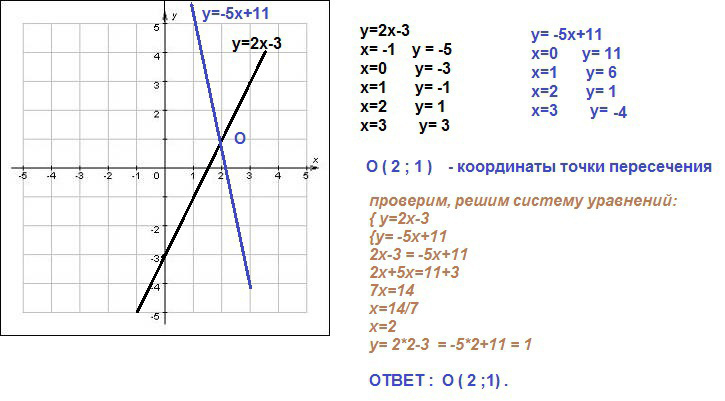
Постройте график функции y=0,8x Найдите координаты точки пересечения этого графика с прямой y=4
Решение: просто выбираете значения х, и по формуле находите унапример подставляете вместо х 0,1,2,3
тогда
у=0
у=0,8
у=1,6
у=2,4
для х = 0,1,2,3 соотв.
на графике ставите эти точки и соединяете прямой
подставим вместо у четыре: получаем
4=0,8х
решаем и находим х=5
Постройте график функции. y=2x-3 Найдите координаты точки пересечения этого графика с прямой y=-5x+11
Решение: Чтобы найти координаты точки пересечения этого графика, просто приравняй оба графика те 2x-3 =-5x+11одна точка А, точка (2;1)
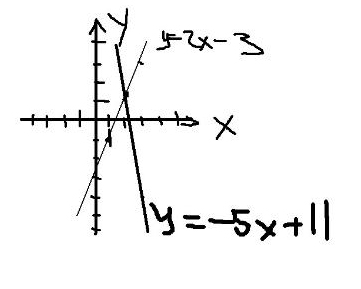
Постройте график функции y=3x-5
Найдите координаты точки пересечения этого графика с прямой y=x+83
Решение: Чтобы найти точки пересечения графиков надо чтобы с левой стороны уравнений стоял только У
дальше надо приравнять
3х-5=х+83 Х переносим влево, все остальное вправо
3х-х=83+5
2х=88
х=44 это мы нашли координату Х точки пересечения
Теперь же найдем координату У
Для этого надо в любое из уравнений подставить найденное значение Х
у=3*44-5
у=127 координата У
Ответ: точка пересечения (44;127)



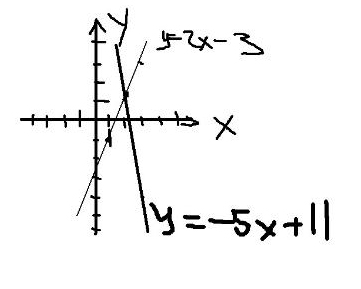
 Декартова система координат
Пусть в пространстве заданы две различные произвольные точки О и М, и пусть одна из них, например точка О, выбрана в качестве начальной. Тогда вектор \(\vec{OM}\) называется радиус-вектором точки М относительно точки О (рис.).
Пусть в пространстве задана точка О и некоторый базис e1, e2 , e3. Совокупность этого базиса и точки О называется декартовой системой координат О,...
Декартова система координат
Пусть в пространстве заданы две различные произвольные точки О и М, и пусть одна из них, например точка О, выбрана в качестве начальной. Тогда вектор \(\vec{OM}\) называется радиус-вектором точки М относительно точки О (рис.).
Пусть в пространстве задана точка О и некоторый базис e1, e2 , e3. Совокупность этого базиса и точки О называется декартовой системой координат О,... Выбором прямоугольной декартовой системы координат устанавливается взаимно однозначное соответствие между точками плоскости и упорядоченными парами действительных чисел. Это означает, что каждой точке плоскости соответствует единственная пара чисел и каждой упорядоченной паре действительных чисел соответствует единственная точка.
Выбор той или иной системы координат ничем не ограничен и определяется в каждом конкретном случае только соображениями удобства. Часто одно и то же множество приходится...
Выбором прямоугольной декартовой системы координат устанавливается взаимно однозначное соответствие между точками плоскости и упорядоченными парами действительных чисел. Это означает, что каждой точке плоскости соответствует единственная пара чисел и каждой упорядоченной паре действительных чисел соответствует единственная точка.
Выбор той или иной системы координат ничем не ограничен и определяется в каждом конкретном случае только соображениями удобства. Часто одно и то же множество приходится...