координаты »

найдите координаты точки - страница 3

  • Функция задана формулой y=-3х-4. Найдите координаты точки пересечения графика этой функции с осью ординат


    Решение: У=-3х-4
    х 1 2 
    ______
    у -1 -10
    система координат(надеюсь поймете)
     
      у
      1
      -1. 1 2 х 
      -1 *
      -2
      -3
      -10 *
    По * проводите прямую и подписываете ее как у=-3х-4

  • Найдите координаты точки пересечения с осями координат графика функции y=2x+4


    Решение: Y=2x+4 - функция вида y=kx+m, где коэффициент m обозночает точку пересечения с осью ординат, т. е. график пересекает ось ординат в точке (0;4).
    2x+4=0
    2x=-4
    x=-2
    В точке (-2;0) график пересекает ось абсцисс.
    Ответ: (0;4) точка пересечения графика с осью ординат
    (-2;0) точка пересечения графика с осью абсцисс

  • , не понимаю эти функции График функции y=3x^2 - 5x - c проходит через точку (-3;-5). Найдите координаты точки пересечения графика с осью ординат


    Решение: Чтобы найти точку пересечения графика вашей функции с осью ординат, нужно вместо значения х в вашей функции подставить 0. Т. к. При пересечении функции с осью ординат х=0. у=-с. 
    А чтобы найти с, нужно вместо х в это уравнение подставить-3, а вместо у -5. И вы найдете с. 
    С=47.
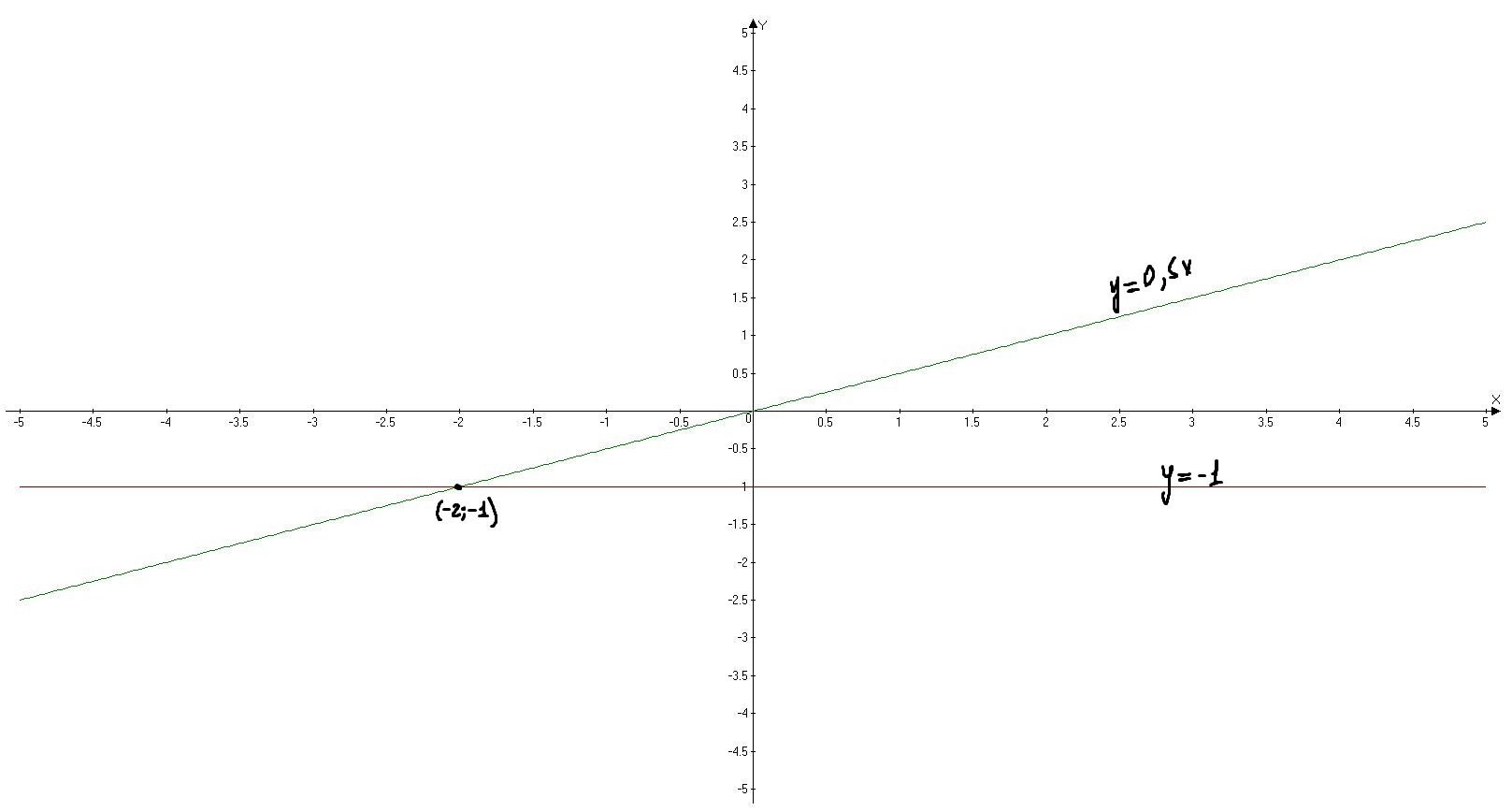
    значит точка пересечения с осью ординат будет (0;-47)

  • Постройте график функции y=0,5x. Найдите координаты точки пересечения этого графика с прямой y=-1.


    Решение:

    y=0.5x 

    Берете и подставляете 3 любые точки, например 0,1, и -1, в уравнение 

    0,1 и -1 это х, подставляете эти значения(0,1 и -1) в уравнение и получаете точки с координатами(0;0),(1;0,5) и (-1;-0,5) отмечаете эти точки на координатной прямой, затем соединяете эти точки и получаете прямую-это и есть график уравнения у=0,5х Затем чертите прямую у=1 эта прямая параллельна оси х, затем находищь точки пересечения графиков у=1 и у=0,5 точка пересечения и есть ответ на твой вопрос (в ответе записывай только координату х)

    y . x  Берете и подставляете любые точки например и - в уравнение  и - это х подставляете эти значения и - в уравнение и получаете точки с координатами и - - отмечаете эти точ...

  • Постройте график функции у=3х-5
    найдите координаты точки пересечения этого графика с прямой у=-5х+11


    Решение: Могу привсти аналитическое решение:

    Так как точка пересечения общая для этих прямых, то мы можем уравнять их правые части:

    3х-5=-5х+11 - решаем это уравнение

    8х=16

    х=2 - мы нашли координату икс и теперь можем найти у. Подставляем полученное значение в первое уравнение:

    у=3*2-5=1

    Точка пересечения - (2; 1)

<< < 123 4 5 > >>