найдите координаты точки - страница 5
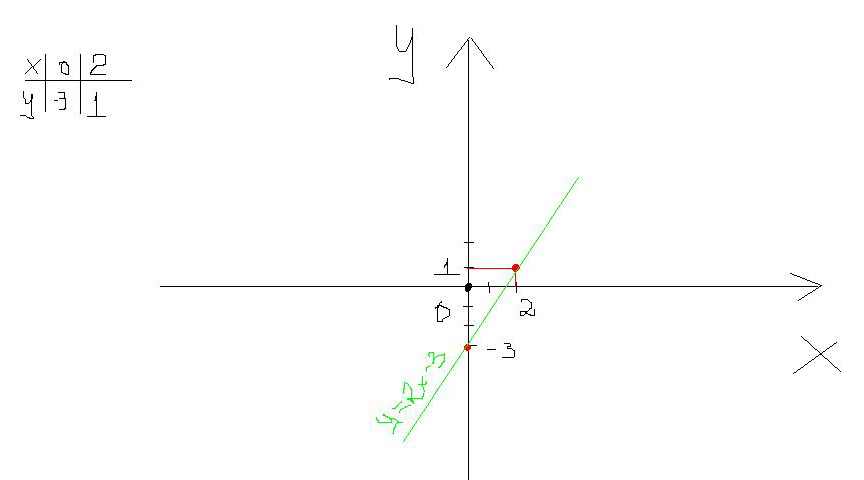
Постойте график функции у=2х-3. Найдите координаты точки пересечения этого графика с прямой у=5х+11
Решение: Это линейная функция, следовательно ее графиком будет прямая. Чтобы изобразить ее, нам надо найти 2 точки этой прямой. Для этого подставим в функцию значение х (обычно всегда ставят ноль и например 1 или 2, т. к. легче маленькое число, а ноль всегда ставят, так просто легче чертить ) и получили "у" -3 и 1 соответственно.Далее найдем точку пересечения прямых. Для этого нам не надо строить вторую прямую мы просто приравняем 2х-3=5х+11 (т. к. у=у ну например 10=5+5 и 10 =7+3 в итоге то 5+5=7+3 и решаем это
2х-5х=11+3
3х=-14
х=-4целых 2/3
подставим в любую функцию
у=2*(-4 2/3) - 3
у=-12 целых 1/3
Ответ: (-4 2/3; -12 1/3)
Постройте график функции y=2x-3 и найдите координаты точки пересечения этого графика с прямой y=-5x+11
Решение: Графики заданных функций - это прямые линии.
Для построения прямой достаточно определить координаты двух точек:
у = 2х - 3
Задаём любую координату: например, х = 0 у = 2*0 - 3 = -3.
Получили координаты первой точки.
Задаём другое значение х = 3 у = 2*3 - 3 = 6 - 3 = 3.
То же самое нужно выполнить для второй прямой:
у = -5х + 11
х = 0 у = -5*0 + 11 = 11
х = 4 у = -5*4 + 11 = -20 + 11 = -9.
После построения прямых находится точка их пересечения.
Координаты этой точки можно проверить аналитически.
Для этого надо решить систему линейных уравнений:
у = 2х - 3 у = 2х - 3
у = -5х + 11 -у = 5х - 11
0 =7х - 14 7х = 14 х= 14/7 = 2 у = 2*2 - 3 = 1.
Постройте график функции у=4х-7. Найдите координаты точки пересечения этого графика с прямой у = х + 83
Решение: График этой функции - прямая, поэтому для того, чтобы его построитоь достаточно 2-х точек. Например: х=0, у=-7;х=2, у=1
Чтобы най ти точки пересечения с другой прямой, можно построить 2-ую по 2-м точкам.
Или решить систему
у=4х-7
у=х+83
Подставим вместо у во второе уравнение его значение
4х-7=х+83
3х=90
х=30
у=30+83
у=113
Ответ: точка пересечения (30;113)
График этой функции - прямая, поэтому для того, чтобы его построитоь достаточно 2-х точек. Например: х=0, у=-7;
х=2, у=1
у=4х-7
у=х+83
Подставим вместо у во второе уравнение его значение
4х-7=х+83
3х=90
х=30
у=30+83
у=113
Ответ: точка пересечения (30;113)Постройте графики функций у = 5х и у = -3х + 8. Найдите координаты точки их пересечения
Решение: 1) график
Х=0 у=0
Х=1 у=5
2график
Х=0 у =8
Х=-1 у = 11
По двум точкам стройте и найдете пересечение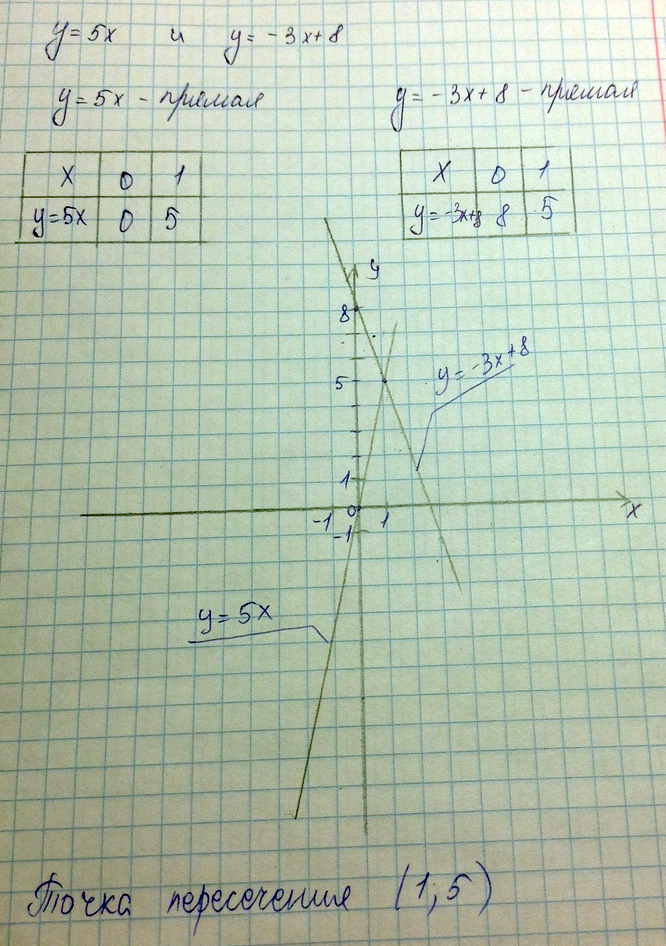
1. Найдите ординату точки, лежащей на графике функции 3х–7=74, если абсцисса этой точки равна 27.
2. Найдите координаты точки пересечения графиков х–у=3,2 и 5х+3у=28,8
Решение: 1) Если точка лежит на прямой, то координаты этой точки удовлетворяют уравнению этой прямой. Другими словами, если координаты подставить в уравнение, то получим верное равенство.
Абсцисса точки ( это координата х) равна 27, Подставим х=27 в уравнение, получим:
3·27-7=74- верно, так как 74=74
Значит точки у которых х=27 а у-любое удовлетворяют уравнению.
Это точки (27; с), где с-любое число.
2) Координаты точки пересечения можно найти графически. Построить две прямые
х-у=3 по двум точкам (0;-3) и (3;0)
5х+3у=28,8 по точкам (0;9,6) и (5,76; 0)
Поскольку координаты второй прямой сложно отметить в системе координат, то
графически решить вряд ли получится.
Решаем задачу алгебраически,
то есть рассмотрим систему двух уравнений:
$$ \left \{ {{x-y=3} \atop {5x+3y=28,8}} \right. \Rightarrow \left \{ {{3x-3y=9} \atop {5x+3y=28,8}} \right. $$
Сложим уравнения, получим 8х=9+28,8
8х=38,4
х=4,8
Подставим х =4,8 в первое уравнение х-у=3, получим: 4,8-у=3, у=4,8-3, у=1,8
Ответ (4,8 ; 1,8)- точка пересечения двух прямых


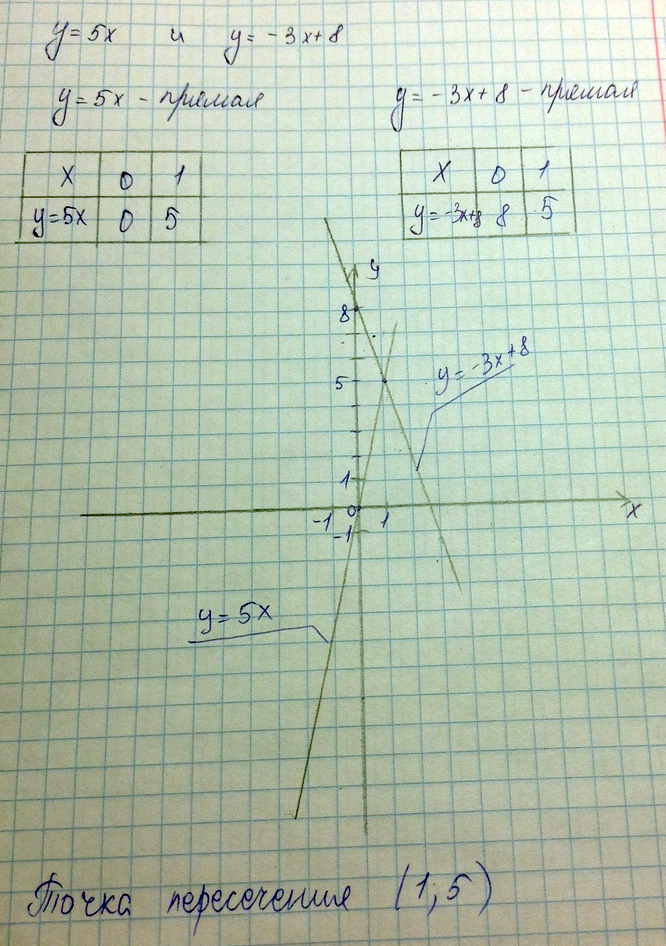
 Декартова система координат
Пусть в пространстве заданы две различные произвольные точки О и М, и пусть одна из них, например точка О, выбрана в качестве начальной. Тогда вектор \(\vec{OM}\) называется радиус-вектором точки М относительно точки О (рис.).
Пусть в пространстве задана точка О и некоторый базис e1, e2 , e3. Совокупность этого базиса и точки О называется декартовой системой координат О,...
Декартова система координат
Пусть в пространстве заданы две различные произвольные точки О и М, и пусть одна из них, например точка О, выбрана в качестве начальной. Тогда вектор \(\vec{OM}\) называется радиус-вектором точки М относительно точки О (рис.).
Пусть в пространстве задана точка О и некоторый базис e1, e2 , e3. Совокупность этого базиса и точки О называется декартовой системой координат О,... Выбором прямоугольной декартовой системы координат устанавливается взаимно однозначное соответствие между точками плоскости и упорядоченными парами действительных чисел. Это означает, что каждой точке плоскости соответствует единственная пара чисел и каждой упорядоченной паре действительных чисел соответствует единственная точка.
Выбор той или иной системы координат ничем не ограничен и определяется в каждом конкретном случае только соображениями удобства. Часто одно и то же множество приходится...
Выбором прямоугольной декартовой системы координат устанавливается взаимно однозначное соответствие между точками плоскости и упорядоченными парами действительных чисел. Это означает, что каждой точке плоскости соответствует единственная пара чисел и каждой упорядоченной паре действительных чисел соответствует единственная точка.
Выбор той или иной системы координат ничем не ограничен и определяется в каждом конкретном случае только соображениями удобства. Часто одно и то же множество приходится...