координаты »

определите координаты точек пересечения графиков - страница 7

  • Решите надо 1; (2х-5)(х+1)=6х
    2; Упростите выражение
    2корень27 - корень 300 - корень12
    3; Найдите координаты точек пересечения графиков функции
    y=Кореньx и y= 2х.


    Решение: $$ (2x-5)(x+1)=6x, \\ 2x^2-9x-5=0, \\ D=121, \\ x_1=-0,5, \ x_2=5. \\ 2\sqrt{27}-\sqrt{300}-\sqrt{12}=2\sqrt{3\cdot9}-\sqrt{3\cdot100}-\sqrt{3\cdot4}=\\=2\cdot3\sqrt{3}-10\sqrt{3}-2\sqrt{3}=6\sqrt{3}-12\sqrt{3}=-6\sqrt{3} \\ \sqrt{x}=2x, \\ x\geq0, \\ 2x-\sqrt{x}=0, \\ \sqrt{x}(2\sqrt{x}-1)=0, \\ \left [ {{\sqrt{x}=0,} \atop {2\sqrt{x}-1=0;}} \right. \left [ {{x=0,} \atop {\sqrt{x}=\frac{1}{2};}} \right. \left [ {{x=0,} \atop {x=\frac{1}{4};}} \right. \\ y_1=2\cdot0=0, \\ y_2=2\cdot\frac{1}{4}=\frac{1}{2}; \\ (0;0), \ (\frac{1}{4};\frac{1}{2}). $$

  • 1. Найдите нули функции y=4x^2+16 (если они существуют) 1) нет нулей 2) -1/2; 1/2; 3) -4; 4; 4) -2; 2
    2. Найдите координаты точек пересечения графиков функций y=2x^2 и y=x+1.
    3. С помощью шаблона параболы y=x^2 Постройте график функции y=(x-1)^2 -4.


    Решение: Для того, чтобы проверить имеет ли функция нули и найти их, приравниваем выражение к нулю:
    4x^2=16
    x^2=4
    x=2; x=-2
    Т. е. ответ 4).
    2) Приравниваем значения функций:
    2x^2=x+1
    2x^2-x-1=0
    Обычное квадратное уравнение, считаем дискриминант:
    D=1+4*2*1
    D=9
    Ищем корни по формуле:
    x1=-1+3/4=1/2=0,5
    x2=-1-3/4=-1
    Это точки по x, ищем точки по y:
    у=0,5+1=1,5
    у=-1+1=0
    Т. е. графики пересекаются в точках A (0,5; 1,5) и B (-1; 0)
    3) Тут максимум могу сказать, куда график уедет, строить не буду:
    Ветви вверх, уедет на 1 клетку вправо и еще на 4 вниз.

  • 1) Исключите иррациональность из знаменателя, что получится ?
    корень из 7 + корень из 3 дробная черта корень из 7 - корень из 3
    2) (х-7)(х+3)+(х-1)(х+5)=102 Решите уравнение пож-та
    3) Найдите все значения а, при которых уравнение ах2+5х+4=0, а больше 0 имеет два корня
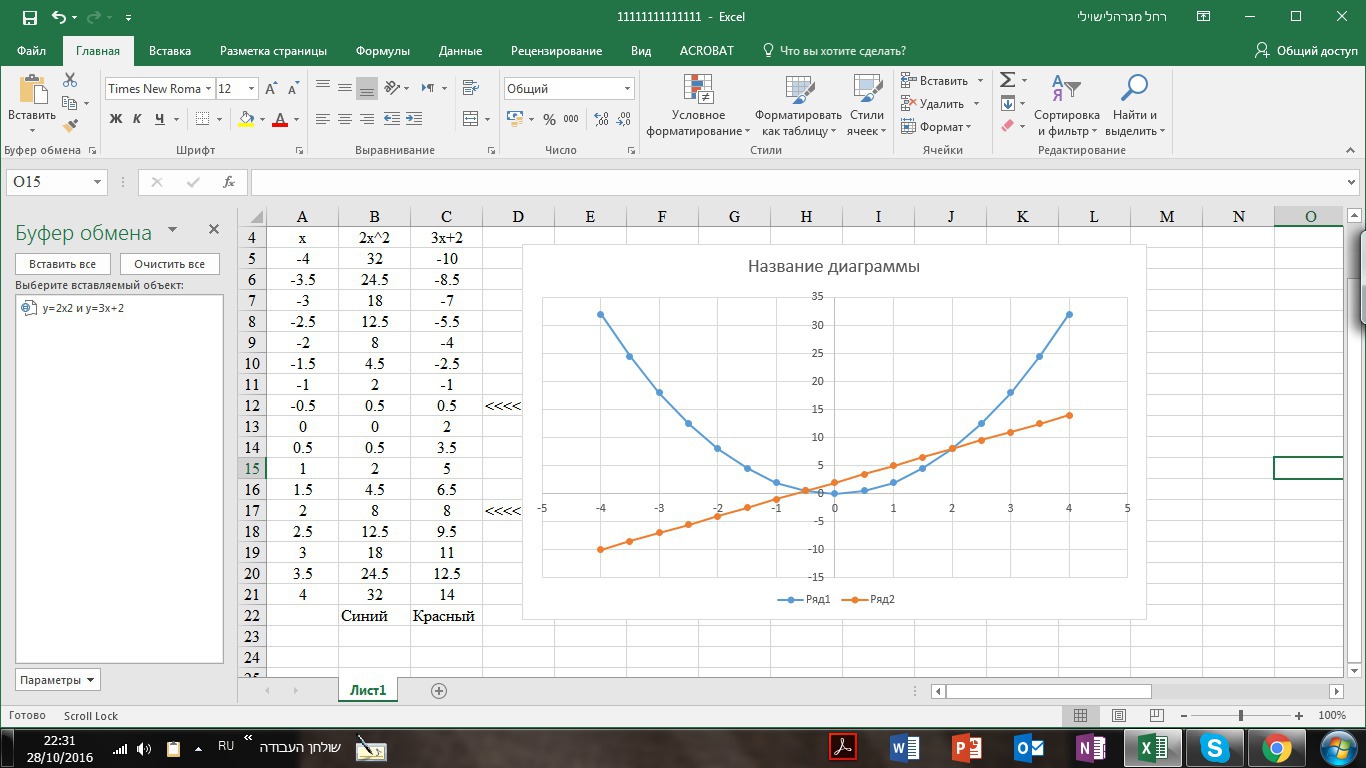
    4) Найдите координаты точек пересечения графиков функций y=2x2 и y=3x+2


    Решение: (√7+√3)/(√7-√3)=
    ((√7+√3)/(√7-√3))²=
    (7+3)/(7-3)=10/4=2.5
    (х-7)(х+3)+(х-1)(х+5)=102 
    (x²+3x-7x-21)+(x²+5x-x-5)-102=0
    2x²-128=0
    x=√64=8
    Во вложении график 4 задания

    √7+√3÷√7-√3=(√7+√3)²÷7-5=(10+2√21)÷4=5+√21÷2
    (х-7)·(х+3)+(х-1)·(х+5)=102
    х²+3х-7х-21+х²+5х-х-5=102
    2х²=128  х²=64 х=8  х=-8
    ах²+5х+4=0   Корни есть, когда D>0 D=в²-4ас    5²-4·4·а>0
    25-16a>0  25>16a  a<25÷16  a<1,9/16

    - - - . х- х х- х   x x- x- x x-x- - x - x Во вложении график задания - - х- х х- х х х- х- х х-х- х   х х   х - ах х    Корни есть когда D gt D в - ас    - а gt - a gt   gt...

  • Укажите промежуток, которому принадлежит сумма корней уравнения (x^2+3*x)/(x-4)=(x^2-х)/(4-х)
    Найдите среднее арифметическое корней уравнения (5*y-2)/(2*y+1)=(3*y+2)/(y+3)
    Найдите среднее арифметическое корней уравнения (7*a-6)/(a^3+27)=1/(a^2-3*a+9)-1/(a+3)
    Найдите координаты точек пересечения графиков функций y=4*x и y=7/(x+1)-1


    Решение: Х2-21+54=0 теперь находим дискрименант:  D=21^2-54*4=441-216=225/                                                    21-15теперь находим корни:  х1=-=3                                          2                                            21+15                                   х2=-=18                                             2 теперь находим среднее арифметическое: 18+3                                                                         -=10,5                                                                    2 Ответ: среднее арифметическое 10,5.

  • 1. Решите уравнение (x^2+3x)/2+(x-3x^2)/8=2x.
    А) 3 Б) 3; 0 В) – 3; 0 Г) 0; - 29
    2. Сумма корней уравнения x^2/(3-x)=2x/(3-x).
    А) √2 Б) 0 В) 2 Г) – 2
    3. Укажите, между какими числами находится сумма корней уравнения (x^2+3x)/(x-4)=(x^2-x)/(4-x).
    А) 0 и 1 Б) – 2 и 5 В) – 9 и – 3 Г) 5 и 20
    Найдите среднее арифметическое корней уравнения (5y-2)/(2y+1)=(3y+2)/(y+3).
    А) 2√2 Б) 3 В) – 3 Г) 8
    4. Найдите произведение корней (или корень, если он единственный) уравнения (4x^2-11x-3)/(3-x)=0.
    А) – 3; 1/4 Б) 2; -1/4 В) 3 Г) -1/4
    5. Решите уравнение (7a-6)/(a^3+27)=1/(a^2-3a+9)-1/(a+3).
    Ответ _____________________
    6. Найдите координаты точек пересечения графиков функций y=4x и y=7/(x+1)-1.
    Ответ _____________________


    Решение: №1
    $$ \frac{x^2+3x}{2} + \frac{x-3x^2}{8} =2x \\ |*8 \\ 4x^2+12x+x-3x^2=16x \\ x^2-3x=0 \\ x(x-3)=0 \\ \left\{{{x=0} \atop {x-3=0}} \right. \\ \left\{{{x=0} \atop {x=3}} \right. \\ \text{Ответ:} 0;3 $$
    №2
    $$ \frac{x^2}{3-x} = \frac{2x}{3-x} \\ x^2=2x \\ x^2-2x=0 \\ x(x-2)=0 \\ \left\{{{x=0} \atop {x=2}} \right. \\ x_1+x_2=2 $$
    №3
    $$ \frac{x^2+3x}{x-4}= \frac{x^2-x}{4-x} \\ \frac{x^2+3x}{x-4} =- \frac{x^2-x}{(x-4)} \\ |*(x-4)^2 \\ (x-4)(x^2+3x)=-(x-4)(x^2-x) \\ -4x^2-8x=0 \\ -4x(x+2)=0 \text{Ответ:} -2;0 $$
<< < 567 8 9 > >>