координаты »

найти координаты

  • Опытные данные сведены в таблицу значений переменных x_i и y_i. построить точки(x_i и y_i) в системе координат Oxy. Подобрать формулу эмпирической зависимости между x и y. Найти по методу наименьших квадратов параметры этой зависимости.Оценить среднеквадратичную погрешность. Построить график эмпирической зависимости.


    Решение: 1)Подобрать формулу эмпирической зависимости между x и y. Для начало по точкам не плохо было бы построить, если построить график то будет что то половины параболы, то есть ее правый кусок симметрично расположенный по оси ОУ .(см график)
    Теперь ограничим наш поиск нахождение зависимости, возможные варианты для меня (как я вижу) это:
    1) Обратная функция ввида     $$ y=a+\frac{b}{x} $$, только ее симметричная часть расположенная 3 четверти отбрасывается 
    2) Экспоненциальная ввида $$ y=e^x $$
     По первому пункту сложность заключается в том что мы должны как можно наименьшие коэффициенты подобрать, но так как нам не говорят как точно будет выглядит сама функция, то есть ее некая параметрическая формула, то мы лите можем ограничиться погрешностью от какой-то прямой аппроксимируема равная данной кривой.Я провел эксперименты по алгоритму (ПО МЕТОДУ НАИМЕНЬШИХ КВАДРАТОВ ДЛЯ ЛИНЕЙНОЙ ФУНКЦИЙ)
    $$ S=0.5+1+1.5+2+2.5+3+3.5+4=18 \\ S=0.54+2.02+6.48+10.9+18.4+28.1+38.4+53.1=157.94 \\ S^2=0.5^2+1^2+1.5^2+2^2+2.5^2+3^2+3.5^2+4^2=51 \\ x_{i}y_{i}=514.41\\ \left \{ {{18a+51b=514.41} \atop {18a+18b=157.94}} \right. \\ a=-2.02\\ b=10.8 \\ y=10.8x-2.02 $$
    Но она далеко не идеальная, по сравнению с экспонентой
    больше всего подходит y=e^x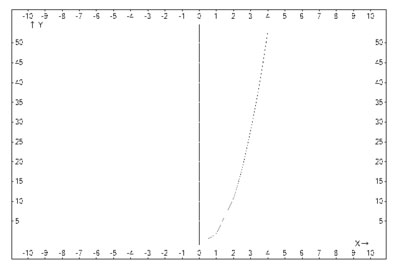    Подобрать формулу эмпирической зависимости между x и y. Для начало по точкам не плохо было бы построить если построить график то будет что то половины параболы то есть ее пра...

  • Как найти координаты точек пересечения параболы и прямой (система): y=x^2-8, x+y=4 ответ есть, главное - решение.


    Решение: y=x²-8

    x+y=4

    y=x²-8

    y=4-x

    x²-8=4-x

    x²+x-12=0

    Δ=1²-4*1*(-12)

    Δ=1+48

    Δ=49

    √Δ=7

    x₁=(-1-7)/(2*1)

    x₁=-8/2

    x₁=-4

    x₂=(-1+7)/(2*1)

    x₂=6/2

    x₂=3

    y₁=4-(-4)

    y₁=8

    y₂=4-3

    y₂=1

    (-4,8),(3,1)

    Из второго уравнения  Y = 4 - X. Подставив это соотношение в первое уравнение, получаем

    X² - 8 = 4 - X

    X² + X - 12 = 0

    X₁ = -4                       X₂ = 3

    Y₁ = 4 - (-4) = 8          Y₂ = 4 - 3 = 1

    Итак, прямая и парабола перескаются в точках  А (-4; 8)  и  В (3; 1)

  • Переходя к полярным координатам, найти площадь, ограниченную линиями: x^2 + y^2 = 2x, x^2 + y^2 = 4x, y = x, y = 0 .


    Решение: 1) Строим фигуру.
    $$ x^{2}+y^2=2x $$
    $$ x^2-2x+1+y^2=1 $$
    $$ (x-1)^2+(y-0)^2=1 $$
    Первое уравнение даёт нам окружность с центром в точке [1,0] и единичным радиусом. Второе даёт нам вторую окружность, по аналогии с первым. Третья функция строится поточечно. Взяв любое значение x, получаем y и проводим прямую. Четвёртая прямая при любом x, даёт y=0.
    Площадь фигуры рассчитывается по формуле $$ S= \int\limits \int\limits{dx} \, dy $$
    При переходе к полярным координатам не забываем dxdy=rdrdφ
    x=rcosφ
    y=rsinφ
    Берём первое уравнение $$ x^2+y^2-2x=0 $$ и осуществляем преобразование (rcosφ)²+(rsinφ)²-2(rcosφ)=0
    Вспоминаем тригонометрическое тождество cosφ²+sinφ²=1 и применяем:
    r²-2rcosφ=0
    r-2cosφ=0
    Ровно по такой же схеме преобразуем x²+y²=4x в r=4cosφ
    Прямая y=x даёт нам изменение угла от 0 до π/4 в полярной системе координат, r же меняется от малой окружности до большей.
    $$ \int\limits^ \frac{ \pi }{4}_0 {} \, d \phi \int\limits^{4cos \phi}_{2cos\phi} {r} \, dr = \int\limits^ \frac{ \pi }{4}_0 {6cos^{2}\phi } \, d \phi =6 \int\limits^ \frac{ \pi }{4}_0 {( \frac{1}{2}cos(2\phi)+ \frac{1}{2} )} \, d \phi= \frac{3(2+ \pi )}{4} $$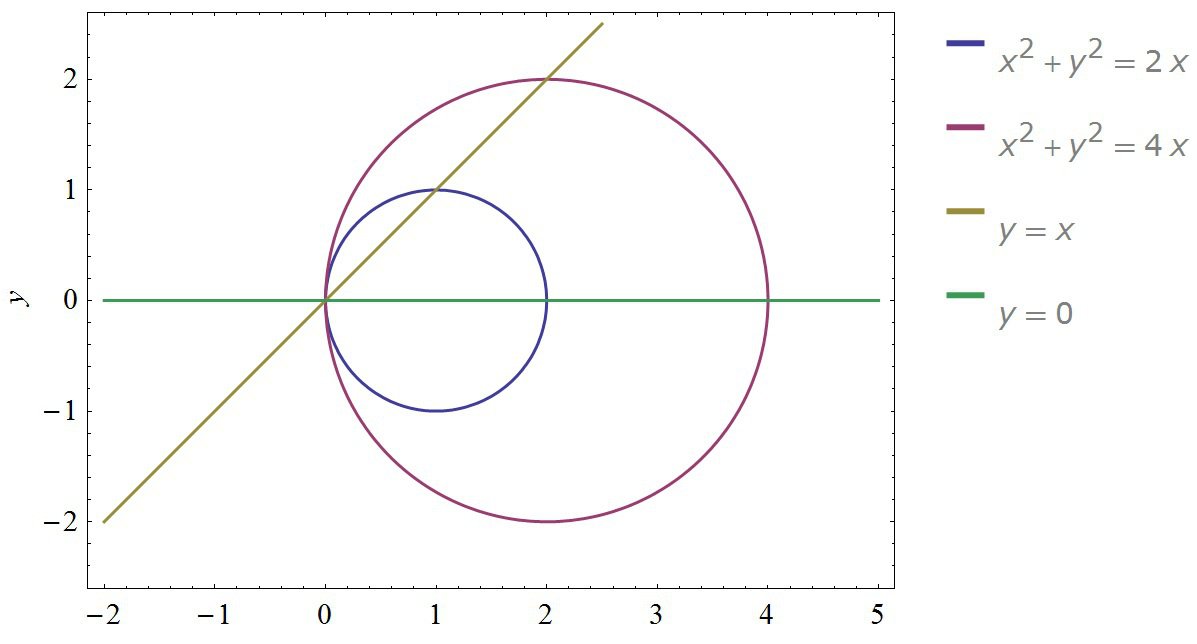Строим фигуру. x y x x - x y x- y- Первое уравнение да т нам окружность с центром в точке и единичным радиусом. Второе да т нам вторую окружность по аналогии с первым. Третья...

  • Координаты точек линейной функции y=x. как их найти?


    Решение: Х в первой степени стоит, значит график - прямая линия, а чтобы ее построить хватит две точки
    Берем любое число для икса, например х=1, подставляй в уравнение свое вместо икса и получите у=1, вот тебе первая точка (1;1), потом бери например, х=2, тогда у=2, вот вторая точка (2;2) и строй график по этим двум точкам

  • Мне дано координаты параболы, а как найти квадратную функцию? Например, вершина(1;0) а переходит в( 0;1) и (2;1)


    Решение: Общий вид квадратичной функции: y = ax^2 + bx + с
    "найти эту функцию" -значит найти ее коэффициенты.
    нужно подставить координаты в общее выражение и решить систему получившихся уравнений.
    1) 0 = a*1^2 +b*1 +с
    2) 1 = 0 + 0 + с
    3) 1 = a*2^2 + b*2 + с
    -
    с = 1
    a+b = -1
    4a+2b = 0
    -
    b = -2a
    a-2a = -1 -> a = 1
    b = -2
    квадратичная функция: y = x^2 -2x + 1

  • дана функция y=kx+b, даны точки координат (-1;1) и (2;3). найти k и b


    Решение: Подставим (-1,1) получим 1 = к*(-1) +в

    Подставим (2,3) получим 3 = к*2 +в

    Осталось решить систему

    в - к = 1

    в + 2к = 3 отнимем от 2 1

    3к = 2 к=2/3

    в = 1+к = 1+2/3 = 5/3

    Искомая прямая у = 2/3 *х + 5/3

    Ну или если красиво, то

    2х - 3у + 5 =0

    а Ответ к задаче, понятно,

    к=2/3 в=5/3

  • Функция y=-1/3x+2 пересекают оси координат в точках А и В. Найти площадь прямоугольного треугольника АОВ, где О - начало координат.


    Решение: О да, это уже по моей части.
    Функция пересекает ось Y тогда, когда x=0. Это будет несложно увидеть, когда мы построим координатную плоскость. Подставим х=0 в функцию, чтобы найти y - то есть у-координату точки пересечения графика с осью.
    $$ y=-\frac{1}{3}\cdot0+2=2 $$
    Итак, точка пересечения с осью Y: $$ (0;2) $$
    Функция пересекает ось X тогда, когда y=0. Значит, чтобы найти х-координату, нам нужно решить простенькое уравнение: $$ 0=-\frac{1}{3}x+2 $$
    Откуда находим $$ x=6 $$
    Точка пересечения с осью X: $$ (6;0) $$
    Вот теперь строим координатную плоскость, две найденные точки и проводим через них прямую. Вообще, если известны 2 точки принадлежащие уравнению прямой, то смело проводим через них линию и получаем наш график.
    Что мы видим? Прямоугольный треугольник! Площадь прямоугольного треугольника равна половине произведения катетов (это ровно половина площади прямоугольника, построенного на этих сторонах - гипотенуза как диагональ будет делить его пополам; помни эту формулу!)
    $$ S=\frac{1}{2}\cdot2\cdot6=6 $$

    О да это уже по моей части.Функция пересекает ось Y тогда когда x . Это будет несложно увидеть когда мы построим координатную плоскость. Подставим х в функцию чтобы найти y -...

  • Найти координат пересечения графика с осью OX и OY
    1)y=3x^2-5x-2
    2)y= -x^2-2x+15


    Решение: При пересечениях координат, одна из переменных, либо аргумент-х, либо функция у равняеться 0
    про пересечении ОХ, у=0, при пересечении OY, х=0;
    ответы в виде (х;0) и (0; У):
    1)
    $$ y=3x^2-5x-2;\\ OX: y=0=3x^2-5x-2;\\ D=b^2-4\cdot a\cdot c=(-5)^2-4\cdot 3\cdot(-2)=25+24=49=7^2;\\ x_1=\frac{-b}{2\cdot a}-\frac{\sqrt{D}}{2\cdot a}=\frac{5}{6}-\frac{7}{6}=-\frac{1}{3};\\ x_2=\frac{-b}{2\cdot a}+\frac{\sqrt{D}}{2\cdot a}=\frac{5}{6}+\frac{7}{6}=2;\\ OY: x=0; y=3\cdot0^2-5\cdot0-2=-2;\\ $$
    значит точки пересечения с ОХ: $$ \left(-\frac{1}{3};0\right) $$ и $$ \left(2;0\right) $$
    c OY:$$ (0;-2) $$
    2)
    $$ y=-x^2-2x+15;\\ OX: y=0=-x^2-2x+15;\\ D=b^2-4\cdot a\cdot c=(-2)^2-4\cdot (-1)\cdot15=4+60=64=8^2; \\ x_1=\frac{-b}{2\cdot a}-\frac{\sqrt{D}}{2\cdot a}=\frac{2}{-2}-\frac{8}{-2}=-1+4=3;\\ x_2=\frac{-b}{2\cdot a}+\frac{\sqrt{D}}{2\cdot a}=\frac{2}{-2}+\frac{8}{-2}=-1-4=-5;\\ OY: x=0; y=-\cdot0^2-2\cdot0+15=15;\\ $$
    значит точки пересечения с ОХ: $$ \left(-5;0\right) $$ и $$ \left(3;0\right) $$
    c OY:$$ (0;15) $$

  • Даны векторы а1 а2 а3 и вектор в, в некотором базисе трехмерного пространства. Показать, что векторы образуют базис данного трехмерного пространства и найти координаты вектора в этом базисе.1.1. (7;2;1), (4;3;5), (3;4;-2), (2;-5;-13).


    Решение: Базис В пространства $$ V $$ состоит из независимых векторов, так, что $$ |\{b_1,b_2,b_k\}|=dimV $$
    Отсюда следует: чтоб доказать что три вектора создают базис для $$ |R^3 $$ нужно показать что векторы независимы. Самый простой для этого способ - привести матрицу состоящую из этих векторов к треугольному виду. По теореме - "ненулевые строки в треугольной матрице - независимы" получим доказательство/опровержение.
    Дальше следует преобразование вектора $$ v $$ по базису В. Самый простой способ это сделать - решить: $$ v= \alpha b_1+ \beta b_2+\gamma b_3 $$ где $$ \alpha, \beta,\gamma \epsilon|R $$ и $$ b_1,b_2,b_3\epsilon B $$

  • Даны четыре вектора а =(1; 2; 1), b =(2; -1; 3), c =(3; -1; 4), e =(5; 1; 6). Показать, что векторы a, b, c образуют базис, и найти координаты вектора e в этом базисе.


    Решение: A,b,c могут считаться базисом, если определитель из столбцов их координат не равен 0.  4 3 -1det( 5 0 4) = -3*(5*2-4*2) - 1*(4*4-(-1)*5) = -27 - не равен 0, значит вектора   2 1 2a,b,c образуют базис, что и требовалось показать. Вектор d представим в виде:d = p*a + q*b + r*cТак как координаты d заданы, получим систему уравнений для коэффициентов p,q,r:4p + 3q - r = 55p + 4r = 72p + q + 2r = 8 q = 8-2p-2r тогда получим систему 2p+7r=19  5p+4r=7Решив, получим: p = -1, r = 3 и тогда q = 4Значит разложение выглядит так:d = -a + 4b + 3c.

1 2 3 > >>