координаты »

найти координаты - страница 2

  • дана функция y=kx+b, даны точки координат (-1;1) и (2;3). найти k и b


    Решение: Подставим (-1,1) получим 1 = к*(-1) +в

    Подставим (2,3) получим 3 = к*2 +в

    Осталось решить систему

    в - к = 1

    в + 2к = 3 отнимем от 2 1

    3к = 2 к=2/3

    в = 1+к = 1+2/3 = 5/3

    Искомая прямая у = 2/3 *х + 5/3

    Ну или если красиво, то

    2х - 3у + 5 =0

    а Ответ к задаче, понятно,

    к=2/3 в=5/3

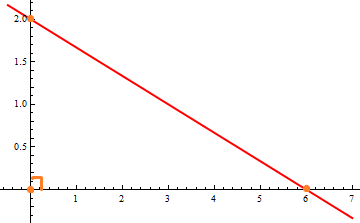
  • Функция y=-1/3x+2 пересекают оси координат в точках А и В. Найти площадь прямоугольного треугольника АОВ, где О - начало координат.


    Решение: О да, это уже по моей части.
    Функция пересекает ось Y тогда, когда x=0. Это будет несложно увидеть, когда мы построим координатную плоскость. Подставим х=0 в функцию, чтобы найти y - то есть у-координату точки пересечения графика с осью.
    $$ y=-\frac{1}{3}\cdot0+2=2 $$
    Итак, точка пересечения с осью Y: $$ (0;2) $$
    Функция пересекает ось X тогда, когда y=0. Значит, чтобы найти х-координату, нам нужно решить простенькое уравнение: $$ 0=-\frac{1}{3}x+2 $$
    Откуда находим $$ x=6 $$
    Точка пересечения с осью X: $$ (6;0) $$
    Вот теперь строим координатную плоскость, две найденные точки и проводим через них прямую. Вообще, если известны 2 точки принадлежащие уравнению прямой, то смело проводим через них линию и получаем наш график.
    Что мы видим? Прямоугольный треугольник! Площадь прямоугольного треугольника равна половине произведения катетов (это ровно половина площади прямоугольника, построенного на этих сторонах - гипотенуза как диагональ будет делить его пополам; помни эту формулу!)
    $$ S=\frac{1}{2}\cdot2\cdot6=6 $$

    О да это уже по моей части.Функция пересекает ось Y тогда когда x . Это будет несложно увидеть когда мы построим координатную плоскость. Подставим х в функцию чтобы найти y -...

  • Найти координат пересечения графика с осью OX и OY
    1)y=3x^2-5x-2
    2)y= -x^2-2x+15


    Решение: При пересечениях координат, одна из переменных, либо аргумент-х, либо функция у равняеться 0
    про пересечении ОХ, у=0, при пересечении OY, х=0;
    ответы в виде (х;0) и (0; У):
    1)
    $$ y=3x^2-5x-2;\\ OX: y=0=3x^2-5x-2;\\ D=b^2-4\cdot a\cdot c=(-5)^2-4\cdot 3\cdot(-2)=25+24=49=7^2;\\ x_1=\frac{-b}{2\cdot a}-\frac{\sqrt{D}}{2\cdot a}=\frac{5}{6}-\frac{7}{6}=-\frac{1}{3};\\ x_2=\frac{-b}{2\cdot a}+\frac{\sqrt{D}}{2\cdot a}=\frac{5}{6}+\frac{7}{6}=2;\\ OY: x=0; y=3\cdot0^2-5\cdot0-2=-2;\\ $$
    значит точки пересечения с ОХ: $$ \left(-\frac{1}{3};0\right) $$ и $$ \left(2;0\right) $$
    c OY:$$ (0;-2) $$
    2)
    $$ y=-x^2-2x+15;\\ OX: y=0=-x^2-2x+15;\\ D=b^2-4\cdot a\cdot c=(-2)^2-4\cdot (-1)\cdot15=4+60=64=8^2; \\ x_1=\frac{-b}{2\cdot a}-\frac{\sqrt{D}}{2\cdot a}=\frac{2}{-2}-\frac{8}{-2}=-1+4=3;\\ x_2=\frac{-b}{2\cdot a}+\frac{\sqrt{D}}{2\cdot a}=\frac{2}{-2}+\frac{8}{-2}=-1-4=-5;\\ OY: x=0; y=-\cdot0^2-2\cdot0+15=15;\\ $$
    значит точки пересечения с ОХ: $$ \left(-5;0\right) $$ и $$ \left(3;0\right) $$
    c OY:$$ (0;15) $$

  • Даны векторы а1 а2 а3 и вектор в, в некотором базисе трехмерного пространства. Показать, что векторы образуют базис данного трехмерного пространства и найти координаты вектора в этом базисе.1.1. (7;2;1), (4;3;5), (3;4;-2), (2;-5;-13).


    Решение: Базис В пространства $$ V $$ состоит из независимых векторов, так, что $$ |\{b_1,b_2,b_k\}|=dimV $$
    Отсюда следует: чтоб доказать что три вектора создают базис для $$ |R^3 $$ нужно показать что векторы независимы. Самый простой для этого способ - привести матрицу состоящую из этих векторов к треугольному виду. По теореме - "ненулевые строки в треугольной матрице - независимы" получим доказательство/опровержение.
    Дальше следует преобразование вектора $$ v $$ по базису В. Самый простой способ это сделать - решить: $$ v= \alpha b_1+ \beta b_2+\gamma b_3 $$ где $$ \alpha, \beta,\gamma \epsilon|R $$ и $$ b_1,b_2,b_3\epsilon B $$

  • Даны четыре вектора а =(1; 2; 1), b =(2; -1; 3), c =(3; -1; 4), e =(5; 1; 6). Показать, что векторы a, b, c образуют базис, и найти координаты вектора e в этом базисе.


    Решение: A,b,c могут считаться базисом, если определитель из столбцов их координат не равен 0.  4 3 -1det( 5 0 4) = -3*(5*2-4*2) - 1*(4*4-(-1)*5) = -27 - не равен 0, значит вектора   2 1 2a,b,c образуют базис, что и требовалось показать. Вектор d представим в виде:d = p*a + q*b + r*cТак как координаты d заданы, получим систему уравнений для коэффициентов p,q,r:4p + 3q - r = 55p + 4r = 72p + q + 2r = 8 q = 8-2p-2r тогда получим систему 2p+7r=19  5p+4r=7Решив, получим: p = -1, r = 3 и тогда q = 4Значит разложение выглядит так:d = -a + 4b + 3c.

<< < 12 3 4 > >>