координаты »

найти координаты - страница 4

  • Найти координаты вектора х, коллинеарного вектору b(9 9 7) и удовлетворяющего условию (x,b)=17


    Решение: Координаты коллинеарных векторов пропорциональны, поэтому можно записать  координаты вектора х ={ 9k; 9k; 7k}.
    Скалярное произведение векторов, заданных своими координатами, равно сумме произведений одноименных координат:
    9k·9+9k·9+7k·7=17
    211k=17
    k=17/211
    Вектор х имеет координаты
    х ={ 9k; 9k; 7k}={153/211;153/211;119/211}

  • Вектор длины 10 приложен в точке (-5;1). Найти координаты вектора, если он состовляет угол в 30 градусов с положительным направлением оси х.


    Решение: y=y0+10*sin30=y0+5=1+5=6

    x=x0+10cos30=-5+5sqrt(3)

    координаты вектора (5;5sqrt(3))

    $$ \vec V = [10, \alpha=30°] = 10 [ cos \alpha, sin\alpha] = 10[\frac {\sqrt3}{2}, \frac 12] = [ {5 \sqrt3}, 5] \approx [8.66, 5 ] $$

    координаты  конца  вектора    =   координаты  приложения плюс вектор :

    $$ (-5, 1 ) + [{5 \sqrt3}, 5] =(({5 \sqrt3} - 5), (6)) \approx (3.660, 6) $$

  • В прямоугольной системе координат Охуz построить точки A (5,1,3), B (2,2,4).

    Найти координаты вектора AB.


    Решение: Использовано определение координат точки в прямоугольной системе координат XOYZ, определение координат вектора, применена формула координат вектора через координаты его начала и конца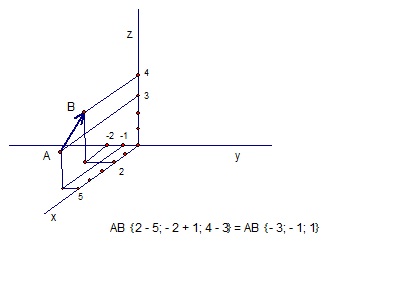

    Использовано определение координат точки в прямоугольной системе координат XOYZ определение координат вектора применена формула координат вектора через координаты его начала...

  • Найти координаты неизвестного вектора а (x; x-2; x-1) еще дан вектор в(1: 3; 4)
    Как найти неизвестный вектор?


    Решение: Предположим векторы a и b - противоположные стороны. Тогда необходимо достаточно чтобы их длины были равны, а сами они были коллинеарны. Но даже условие коллинеарности для этих векторов не может быть выполнено, так как система 
    {x=k
    {x-2=3k
    {x-1=4k
    Не имеет решений.
    Остается второй вариант, прямоугольник построен на а и b как на соседних сторонах, тогда необходимо и достаточно, чтобы они были перпендикулярны, а это условие в свою очередь эквивалентно условию равенства нулю скалярного произведения, то есть x+3(x-2)+4(x-1)=0, то есть 8x=10, x=5/4.

  • Дано: вектор m{-6;2), вектор n{-1;-2}, c = одна вторая(1/2) вектора m + вектор n.
    Найти: а) координаты вектора с; б) длину вектора с


    Решение: $$ \vec c = \frac{1}{2}\vec m+\vec n=( \frac{1}{2}*(-6)+(-1); \frac{1}{2}*2+(-2))=(-4;-1) \\ \vec c(-4;-1) \\ \\ |\vec c|= \sqrt{x^2+y^2}= \sqrt{x} \sqrt{(-4)^2+(-1)^2}= \sqrt{16+1}= \sqrt{17} \\ |\vec c|=\sqrt{17} $$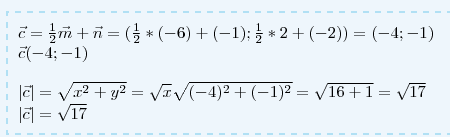

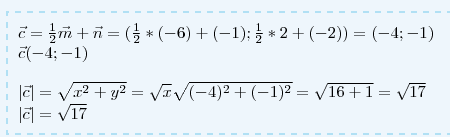
    vec c frac vec m vec n frac - - frac - - - vec c - - vec c sqrt x y sqrt x sqrt - - sqrt sqrt vec c sqrt...
<< < 234 5 6 > >>