в одной и той же системе координат постройте - страница 5
1 Функция задана формулой: у=4х-30.
Определите:
а) значение у, если х= -2,5
б) значение х, при у= -6
в) проходит ли график функции через точку В(7; -3) ?
2. постройте график функций у=-3х+3 укажите с помощью графика, при каком значении х значение у равно 6
3. В одной и той же системе координат постройте графики функций: у=0,5х и у=-4
4. Найдите координаты точки пересечения графиков функций: у=-38+15 и у= -21х-36
5. Задайте формулой линейную функцию, график которой параллелен прямой у=-5х+8 и проходит через начало координат.
Решение: а) у=-40б) х=0,6
в) нет так как координата х=7 у должен быть равен -2
4*(7)-3=-2
2) у=6 при х = -1 у=-3*(-1)+3=6
3) у=-4 прямая линия параллельная оси ох проходит через точку с кор(0:-4)
у=0,5х подставляй любые х и получишь координаты
например х=2 тогда у равно 1 точка (2:1) и х=4 тогда у= 2 координаты точки(4:2)
через эти точки проведи прямую
4) у=-38+15 и у=-21х-36 где то ты потеряла х в первом уравнении вероятно уравнение такое у=-38х+15 тогда
-38х+15=-21ч-36
-38х+21х=-36-15
-17х=-51
х=-3
следовательно у= -38*(-3)+15=129
точка пересечения (-3:129)
а) вместо х подставь -2,5, найдете у
б) вместо у подставь -6, найдете х
в) вместо х подставь 7, а вместо у -3
2. начерти таблицу со значениями х и у, напиши любой х и по формуле найдете у.
а потом по графику посмотрите значение
3. у=0,5х - опять черти таблицу, подставь х, найдете по формуле у, а у=-4 - это прямая параллельная оси х
4. у=-38+15 ; у=-23(прямая)
у=-21х-36(опять таблица и как во всех остальных случаях)
С Д. З
1). Функция задана формулой у = - 5х + 10. Определите:
а). Чему равно значение у при х = 2,5 ;
б). При каком значении х значение у равно – 5;
в). Проходит ли график функции через точку
В ( 3; 5 ).
2). Постройте график функции у = – 2 х + 6.
Укажите с помощью графика, при каком значении х значение функции равно – 2.
3). В одной и той же системе координат постройте графики функций у = 0,5х и у = - 4. Определите координаты точки пересечения графиков.
4). Найдите значение k, если известно, что график функции у = kх – 12 проходит через точку А ( 15; - 7 ).
5). Запишите уравнение прямой, параллельной графику функции у = 8х + 13 и проходящей через начало координат.
Решение: 1)y=-5x+10
а)x=2,5⇒y=-5*2,5+10=-12,5+10=-2,5
b)y=-5⇒-5x+10=-5⇒-5x=-15⇒x=3
c)B(3;5)
-5*3+10=-15+10=-5 -5≠5 не проходит
2)y=-2x+6
x 0 4
y 6 -2
график
3) у=0,5х прямая в 1 и 3 четверти
х 0 -8
у 0 -4
у=-4 прямая параллельная оси ох
точка (-8;-4)
график
4)y=kx-12 A(15;-7)
-7=15k-12
15k=-7+12=5
k=5/15=1/3
y=1/3*x-12
5)y=8x+13
Функция имеет вид у=кх, если параллелен данному, то к=8
у=8х
№1 Функция задана формулой y=4x-30. Определите:
а) значение y, если x=-2,5; б) значение x, при котором y=-6; в) проходит ли график функции через точку B(7;-3).
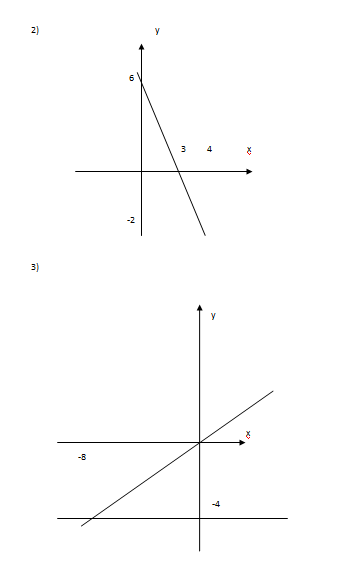
№2 а) Постройте график функции y=-3x+3.
б) Укажите с помощью графика, при каком значении x значение y равно 6.
№3 В одной и той же системе координат постройте графики функции: а) y=0,5x; б) y=-4
№4 Найдите координаты точки пересечения графиков функции y=-38x+15 и y=-21x-36
№5Задайте формулой линейную функцию, график которой параллелен прямой y=-5x+8 и проходит через начало координат
Решение: №1а у=4*(-2,5)-30 (Подставила в формулу)
у= -10-30=-10+(-30)= -40
б) 4х-30=-6(Подставила в формулу)
4х= -6+30(Перенесла из одной части уравнения в другую, сменив знак)
4х=24( Затем делим обе части на 4)
х=6
в) В(х, у)- координаты точки В
В(7,3) Значит: х=7, у=-3
Затем подставляем х и у в формулу:
-3=4*7-30
-3=28-30
-3=-2- не верно, значит прямая не проходит через точку В
Построить в одной и той же системе координат графики функций y=x квадрат и y=x+2 найдите с помощью графика функции координаты точек пересечения этих графиков
Решение: Для начала нужно приравнять оба графика
потом находятся х1 и х2 точки пересечения осями х
затем подставляете в любое уравнение и находите точки пересечения с осями у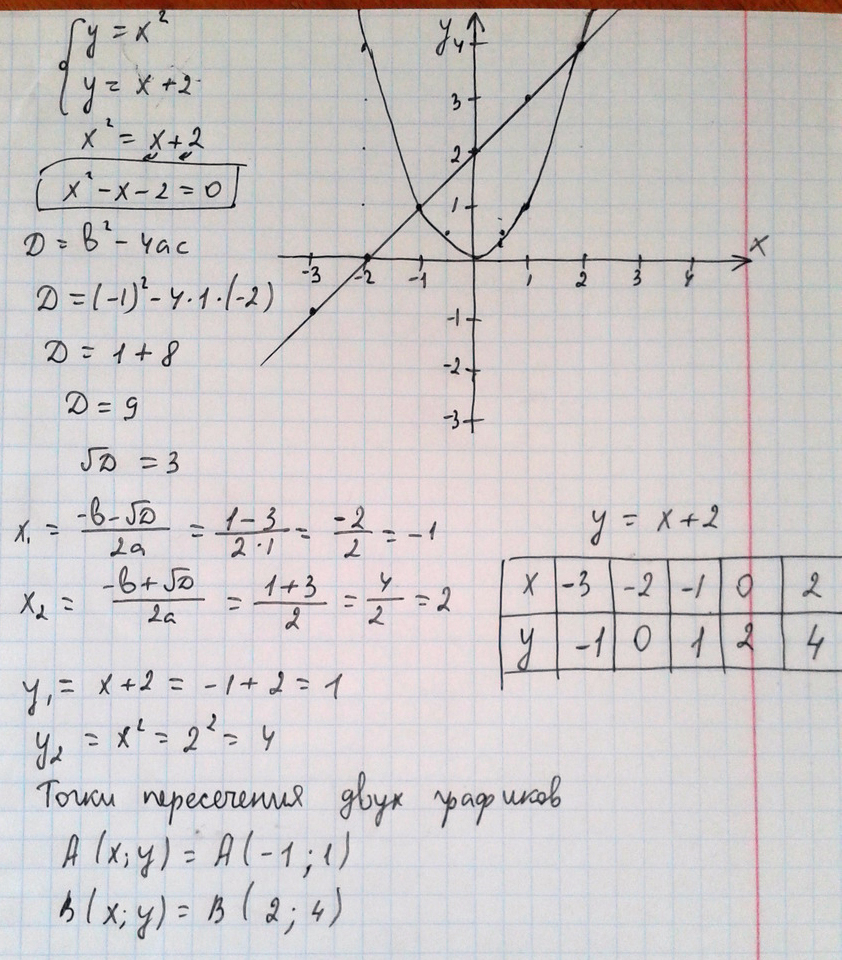
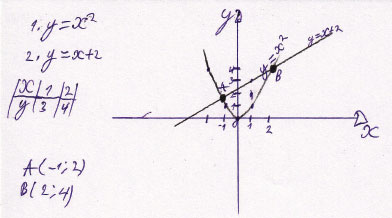
Постройте в одной и той же системе координат графики функций у=х во 2 степени и у=х+2 Найдите с помощью графиков функций координат точек пересечения этих графиков
Решение: Точки пересечения:A(-1;2) и B(2;4)


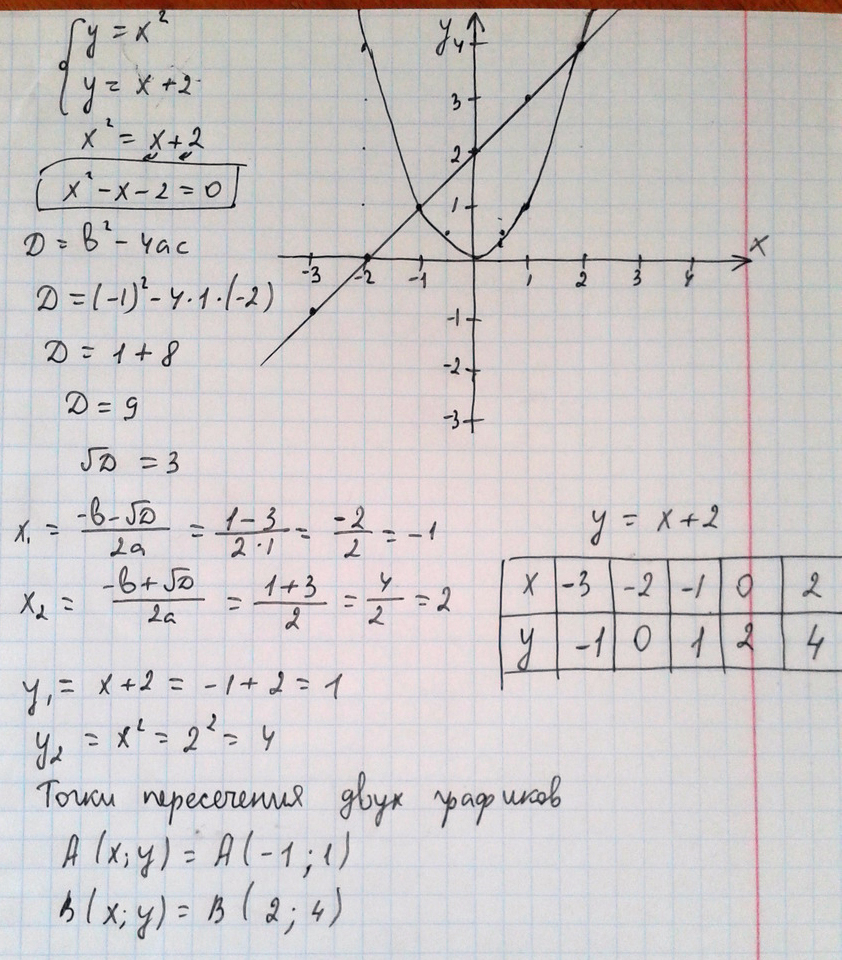

 Декартова система координат
Пусть в пространстве заданы две различные произвольные точки О и М, и пусть одна из них, например точка О, выбрана в качестве начальной. Тогда вектор \(\vec{OM}\) называется радиус-вектором точки М относительно точки О (рис.).
Пусть в пространстве задана точка О и некоторый базис e1, e2 , e3. Совокупность этого базиса и точки О называется декартовой системой координат О,...
Декартова система координат
Пусть в пространстве заданы две различные произвольные точки О и М, и пусть одна из них, например точка О, выбрана в качестве начальной. Тогда вектор \(\vec{OM}\) называется радиус-вектором точки М относительно точки О (рис.).
Пусть в пространстве задана точка О и некоторый базис e1, e2 , e3. Совокупность этого базиса и точки О называется декартовой системой координат О,... Выбором прямоугольной декартовой системы координат устанавливается взаимно однозначное соответствие между точками плоскости и упорядоченными парами действительных чисел. Это означает, что каждой точке плоскости соответствует единственная пара чисел и каждой упорядоченной паре действительных чисел соответствует единственная точка.
Выбор той или иной системы координат ничем не ограничен и определяется в каждом конкретном случае только соображениями удобства. Часто одно и то же множество приходится...
Выбором прямоугольной декартовой системы координат устанавливается взаимно однозначное соответствие между точками плоскости и упорядоченными парами действительных чисел. Это означает, что каждой точке плоскости соответствует единственная пара чисел и каждой упорядоченной паре действительных чисел соответствует единственная точка.
Выбор той или иной системы координат ничем не ограничен и определяется в каждом конкретном случае только соображениями удобства. Часто одно и то же множество приходится...