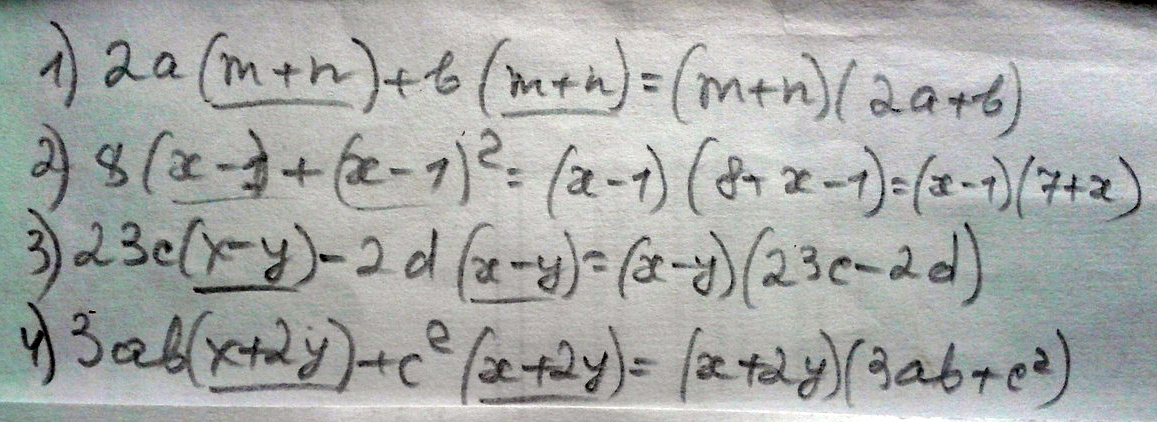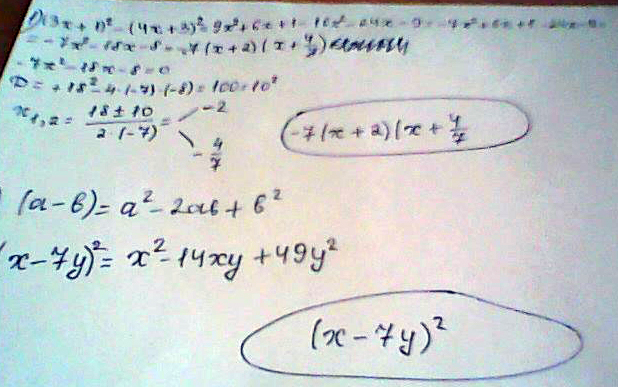разложить многочлен на множители - страница 19
I. Разложите на множители многочлены:^-значит степень
а).a^2+ad-a-d
b).y^3-xy^2+y-x
B).3ab-b^2+3a^2-ab
г).6y^2-3y+2ay-a
II. Разложите на множители:
a).ax-a+bx-b+cx-c
b).ax+bx-ay-by+az+bz
B).ax-bx-x+ay-by-y
III. Сократите дроби:^-значит степень
ax-ay-bx-by
а).
x^2+xy
ax-ay-x^2+xy
B).
ax-a^2
Решение: 1. a) a^2 + ad - a - d = (a^2 - a) + (ad - d) = a(a - 1) + d(a -1) = (a - 1)(a+d)b) y^3 - xy^2 + y - x = (y^3 + y) - (xy^2 + x) = y(y^2 + 1) - x(y^2 + 1) = (y^2 + 1)(y - x)
c) 3ab - b^2 + 3a^2 - ab = (3ab + 3a^2) - (b^2 + ab) = 3a(b + a) - b(b+a) = (3a - b)(b + a)
d) 6y^2 - 3y + 2ay - a = (6y^2 - 3y) + (2ay - a) = 3y(2y - 1) + a(2y - 1) = (3y + a)(2y - 1)
2. a) ax - a + bx -b + cx - c = a(x - 1) + b(x - 1) + c(x -1) = (a+b+c)(x - 1)
b) ax + bx - ay - by + az + bz = x(a+b) - y(a+b) + z(a + b) = (a + b)(x + z - y)
c) ax - bx - x + ay - by - y = x(a - b - 1) + y(a - b - 1) = (x + y)(a - b - 1)
3. b) (ax - ay - x^2 + xy) / (ax - a^2) = ( (a-x - a)(y - x)) / (a(x - a)) = (y - x) / a
Раскройте скобки:
-2(5а+2в)(2в-5а)
Решение: Правило сокращенного умножения: разность квадратов двух чисел равна произведение разности этих чисел на их сумму и наоборот: произведение суммы двух чисел на их разность равно разности квадратов этих чисел, значит (5a+2b)(2b-5a)=(4b^2-25a^2), отсюда: (-2(5a+2b)(2b-5a))=-2(4b^2-25a^2)=50a^2-8b^2
Нужно представить выражения в виде произведения двух многочленов.
1) 2a(m+n)+b(m+n);
2) 8(x-1)+(x-1)^2
3) 23c(x-y)-2d(x-y)
4) 3ab(x+2y)+c^2(x+2y)
5) 9a^2(x-2y)-b^2(x-2y)+(x-2y)^2
6) 3a(2x-7)+5b(2x-7)-(2x-7)
Решение: Решаем через вынесение общего множителя.$$ 1)\; 2a(m+n)+b(m+n)=(m+n)(2a+b)\\\\2)\; 8(x-1)+(x-1)^2=(x-1)(8+x-1)=(x-1)(x+7)\\\\3)\; 23c(x-y)-2d(x-y)=(x-y)(23c-2d)\\\\4)\; 3ab(x+2y)+c^2(x+2y)=(x+2y)(3ab+c^2)\\\\5)\; 9a^2(x-2y)-b^2(x-2y)+(x-2y)^2=(x-2y)(9a^2-b^2+x-2y)\\\\6)\; 3a(2x-7)+5b(2x-7)-(2x-7)=(2x-7)(3a+5b-1) $$
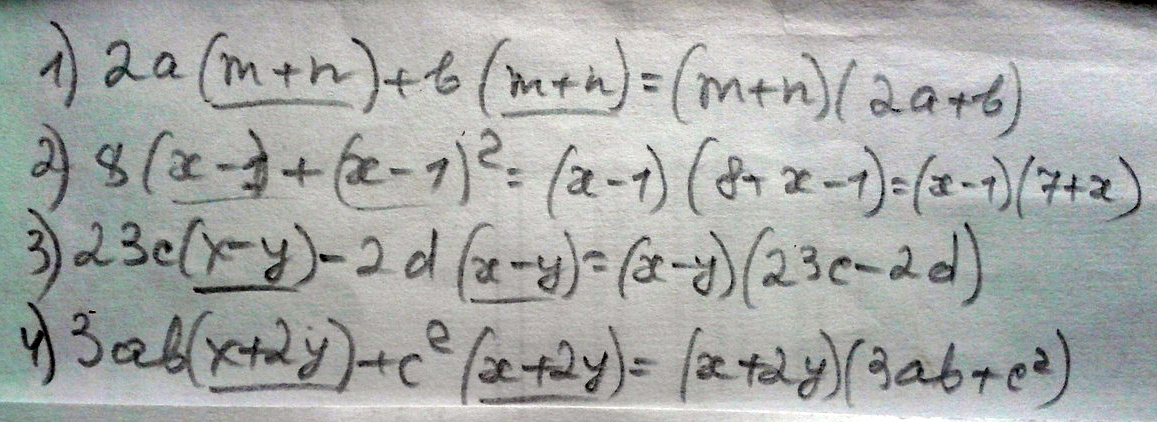
Представить выражение в виде квадрата двучлена:
x^2-14xy+49y^2
Разложить многочлен на множители:
(3x+1)^2-(4x+3)^2
Решение:
1) x^2-14xy+49y^2 = (x-7y)^2
2) (3*x+1)^2-(4*x+3)^2 = -7*x^2+6*x+1-24*x-9 = -7*x^2-18*x+1-9 = -7*x^2-18*x-8 =
-7*(x+2)(x+4/7)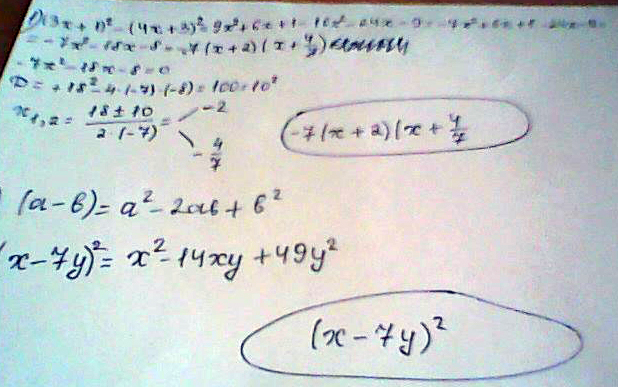
многочлен х3-5х+2 разложили на множители какие из представленных многочленов являются этими множетелями? А) х2+2х-1 Б) х-2 В) х+2 Г) х2-2х+1
Решение: А и б, так как (x2+2x-1)(x-2) равен x3+5x+2Разложить многочлен на множители - это значит представить его в виде (х-х1)(х-х2).(х-хn), где х1, х2. корни многочлена.
Корнями многочлена являются делители его свободного члена. 2: +1,1, +2,2.
+1 и -1 не подходит,2 тоже. Остается +2.
Разделим x^3-5x+2 на х-2 получим x^2+2 x-1 - уравнение, которое в принципе тоже имеет действительные корни x1 = -1-sqrt(2) и x2 = -1+sqrt(2).
Таким образом: x^3-5x+2 = (x-2) (x^2+2 x-1) = (x-2) (x+1-sqrt(2)) (x+1+sqrt(2))