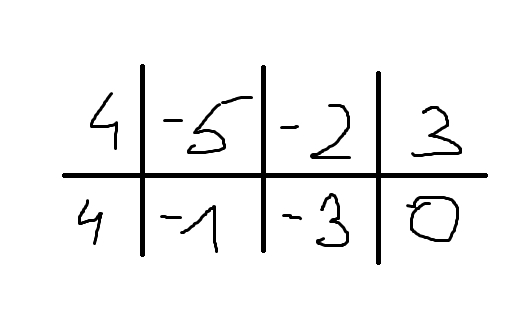многочлен »

корни многочлена - страница 4

  • Сумма коэффициентов произвольного многочлена c целыми коэффициентами равна заданному простому числу p.
    Известно что многочлен имеет более 1 натурального корня. Найдите натуральные корни многочлена.


    Решение: Многочлен имеет вид (х-х1)(х-х2).(х-хn)(x^2k+f)=0
    тогда (1-х1)(1-х2).(1-хn)(1+f)=p - простому числу
    это возможно если
    (1-хi)=1- (a корней);
    (1-хj)=-1-(b корней);
    (1-хn)=p*(-1)^b - единственный корень
    (1+f)=1;f=0;x=0
    среди корней могут быть целые числа 0;2;1-p или 1+p
    так как корень не единственный и корни натуральные (положительные), то остается 2-нечетное число корней и 1+p - один корень

  • Указать кратность всех корней многочлена А(х)=4х³-5x²-2x+3


    Решение: 4*1³-5*1²-2*1+3=0

    4-5-2+3=0

    0=0 ⇒ 1 является корнем многочлена 

    схема Хорнера

    4x²-x-3=0

    4x²-4x+3x-3=

    4x(x-1)+3(x-1)=0

    (4x+3)(x-1)=0

    x=-3/4 ∨ x=1

    1 - двукратный корень

    -3/4 - однократный корень

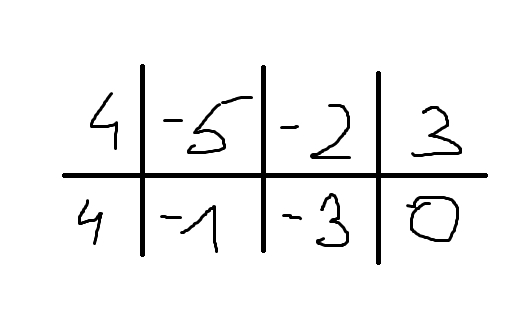
    - - - - является корнем многочлена  схема Хорнера x -x- x - x x- x x- x- x x- x - x - двукратный корень - - однократный корень...

  • Найти сумму и произведение корней многочлена Р(х)=-2х3 + 3х2-6х + 1


    Решение: A = -2, b = 3, c = -6, d = 1
    Делаем замену переменных по формуле x = y - b/3a
    Получаем новое уравнение:
    y^3 +py + q
    где p = -b^2/3a^2 + c/a = 9/4 = 2.25
    a q = 2b^3/27a^3 - bc/3a^2 + d/a = 3/4 = 0.75
    Q = (p/3)^3 + (q/2)^2 > 0 - значит есть один действительный корень и 2 комплексно-сопряженных (которые в данном случае не нужны)
    По формулам Кардано находим корень:
    х = (примерно) 0.181

  • Найти многочлен наименьшей степени, среди корней которого есть числа 1, 2, 3 и коэффициент при старшей степени равен 1
    Выберите один ответ:
    1)x^3-4x^2+9x-6
    2)x^3+6x^2-13x-3
    3)x^3-6x^2-11x-4
    4)x^3-6x^2+11x-6


    Решение: Корни многочлена - числа, обращающие его при подстановке в ноль, значит составим произведение (х-1)*(х-2)*(х-3), очевидно, если подставлять числа 1, 2, 3 в это выражение, его значение будет равно нулю. Осталось лите раскрыть скобки, умножая их по очереди: (х-1)*(х-2)*(х-3)= (х^2-2х-х+2)*(х-3)= (х^2-3х+2)*(х-3)=x^3-3x^2-3x^2+9x+2x-6=x^3-6x^2+11x-6 Ваш ответ под номером 4

    Сумма корней 1+2+3=6  произведение корней равно 6
    воспользуемся обобщенной теоремой Виета
    для 3-й степени x1+x2+x3=-b  x1*x2*x3=-c
    b=-6  c=-6 таким свойством обладает многочен 4)
    ответ 4)

<< < 234