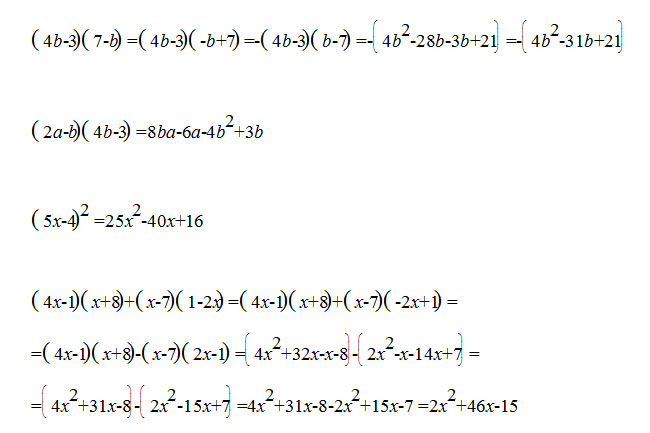многочлен n-й степени - страница 3
Умножение многочлена на многочлен (4в-3)(7-в) (2а-в)(4в-3) (5х-4) всё это в 2 степени
(4х-1)(х+8)+(х-7)(1-2х)
Решение:1) (4в-3)(7-в) = 28в-4в²-27+3в
2) (2а-в)(4в-3)= 8ав-6а-4в²+3в
3) (5х-4)²= 25x² – 40x +16
4) (4х-1)(х+8)+(х-7)(1-2х) = 4x²+32x–x-8+x-2x²–7+14x = 2x²+45x-15
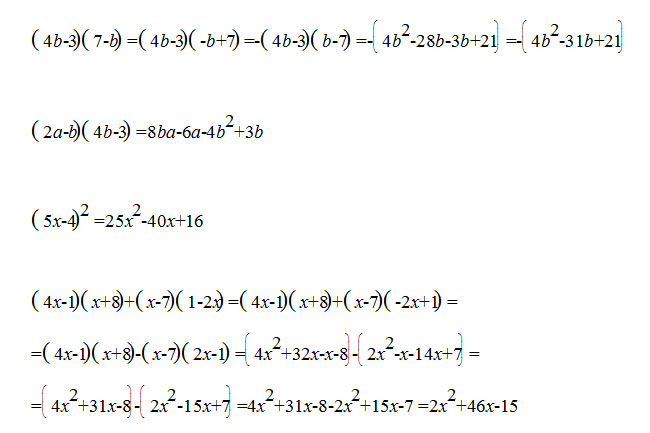
1.Записать в виде многочлена и объяснить аbc+cab (вверху над выражениями— )
2)Какой цифрой заканчивается а )15⁹+26⁹+39⁹ б)99⁹⁹ и еще выше степени ⁹⁹ степень⁹ .Объяснить.
Решение:Abc с чертой вверху ---это запись трехзначного числа...
например, 367 и тогда a=3, b=6, c=7
a --- количество сотен, в выражении запишется как 100*а
b --- количество десятков, в выражении запишется как 10*b
c --- количество единиц, в выражении запишется как 1*с
итак, abc(черта вверху) + cab(черта вверху) =
= 100a + 10b + с + 100с + 10а + b = 100*(a+c) + 10*(a+b) + b+c
2)
15 в любой степени закончится цифрой 5 (т.к. 5*5 = 25)
26 в любой степени закончится цифрой 6 (т.к. 6*6 = 36)
39 в четной степени закончится цифрой 1 (т.к. 9*9 = 81)
в нечетной степени закончится цифрой 9 (т.к. 9*1 = 9)
а) сумма заканчивается цифрой 0 (т.к. 5+6+9 = 20)
б) 99⁹ (в нечетной степени) закончится на 9, т.е. получится вновь нечетный показатель степени
и 99 с нечетным показателем степени закончится на 9Какая степень многочлена?а) 3x8 – x3 – x8 + 6x – 2x8 – 1
И объясните )
Решение: 3x8 – x3 – x8 + 6x – 2x8 – 1 = -x3+6x-1, с наибольшим показателем остается -x3, следовательно степень многочлена 3.$$ 3 x^{8} - x^{3} - x^{8} +6x-2 x^{8} -1=- x^{3} +6x-1 $$
Самая высокая степень у одночлена это 3, значит и степень всего многочлена будет 3
Самое главное, нужно привести выражение в упорядоченный вид и привести подобные, тогда узнаете нужную степень
Ответ: 3Найти степень многочлена а) 6х^2-3х^7+2x^3-x^5+4 в) 4а^2 b-3a^2b^2+5a-14b^2+7
Решение:Степень многочлена - наибольшая из степеней, входящих в него одночленов:
6х^2-3х^7+2x^3-x^5+4
степень 2 7 3 5
а) 7
4а^2 b-3a^2b^2+5a-14b^2+7
степень 3 4 1 2
в) 4
Нужно выбрать один одночлен с наибольшей степенью.
В первом - 3х^7 - степень 7
Во втором - 3а^2b^2 - степень 2+2=4
Какова степень многочлена:3x^8-x^3-x^8+6x-2x^8-1.
Решение: После приведения подобных получим
-x^3 + 6*x - 1,
то есть многочлен ТРЕТЬЕЙ степени.
А в чём, собственно, была проблема? Арифметику забыл? Ведь 3-1-2=0
(Это коэффициенты при x^8).3x^8-x^3-x^8+6x-2x^8-1=-x^3+6x-1
степенью приведенного многочлена называется старшая степень многочлена
в данном случае 3. ответ это многочлен 3 степени