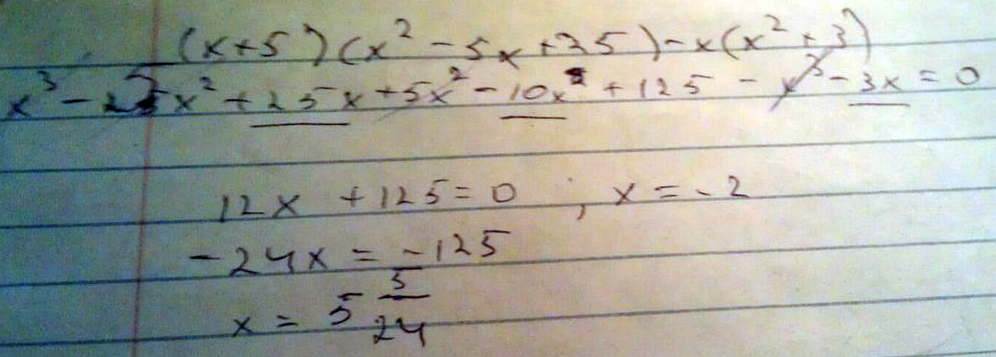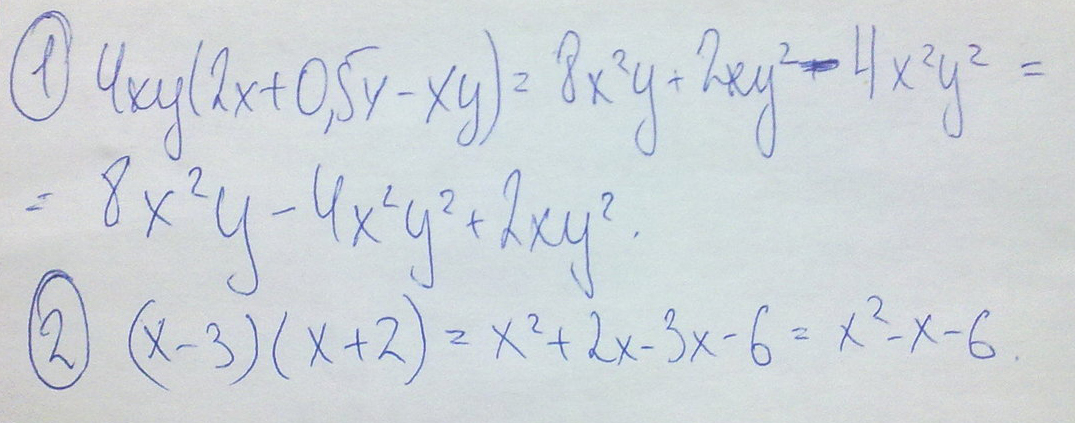многочлен »
преобразуйте выражение в многочлен - страница 18
1. Преобразуйте в многочлен:
a)(x-3)(x+3)-3x(4-x).
б)-4у(y+2)+(y-5)².
в)2(a-3)²-2a².
2. Разложите на множители:
a)x⁴-16x²
б)-4х²-8ху-4у²
3. Упростите выражение и найдите его значение при х=-2:
(Х+5)(х²-5х+25)-х(х²+3).
Решение: 3. Упростите выражение и найдите его значение при х=-2:
(Х+5)(х²-5х+25)-х(х²+3).
Разбор на фотографии1. а) x2-9-(12x-3x2)= x2-9-12x+3x2 = 4x2-6-12x
(p.s. 3x2 - это 3x в квадрате; x2 - x в квадрате и дальше по аналогии)
b) -4y2-8y+y2-10y+25=-3y2-18y+25
v) 2 (a2-6a+9)-2a2= 2a2-12a+18-2a2= -12a+18
2. a) (x2-4x)(x2+4x)
b) -(4x2+8xy+4y2)= -(2x+2y)2 (в квадрате)
3. x3-5x2+25x+5x2-25x+125-x3-3x= 125-3x
если x=-2, то 125-3(-2)= 125+6=131
Надеюсь, правильно.
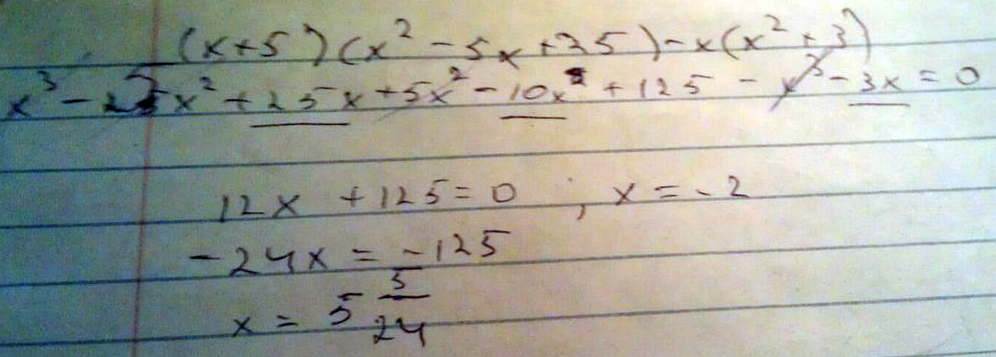
Преобразуйте выражение в многочлен:
(7х-у)(7х+у)
(а-6в)(а+6в)
Представьте в виде произведения:
с^2+2х+1
х^2-14х+49
Решение: 1 формула: a²-b²=(a-b)*(a+b)
a) (7x-y)(7x+y)=(7x)²-y²=49x²-y²;
б) (a-6b)(a+6b)=a²-(6b)²=a²-36b²;
2 формула: ax²+bx+c=a(x-x₁)(x-x₂), где x₁ и x₂ - корни этого уравнения. для нахождения приравнять квадратное уравнение к нулю и найти его корни через дискриминант по формуле D=b₂-4ac; x=(-b=-√D)/2a;
а) x²+2x+1;
x²+2x+1=0;
D=4-4*1=0;
x=(-2+√0)/2=-1. в этом уравнении один корень, т. к. D=0;
a=1; тогда x²+2x+1=(x+1)(x+1);
б) x²-14x+49;
x²-14x+49=0;
D=196-4*49=0;
x=14/2=7;
x²-14x+49=(x-7)(x-7).Преобразуйте заданное выражение в многочлен стардартного вида: 1)4xy(2x+0.5y-xy) 2) (x-3)(x+2)
Решение: Раскроем скобки в каждом случае:1) =8*х^2*y+2*x*y^2-4*x^2*y^2
2) = x^2+2*x-3*x-6=x^2-x-6
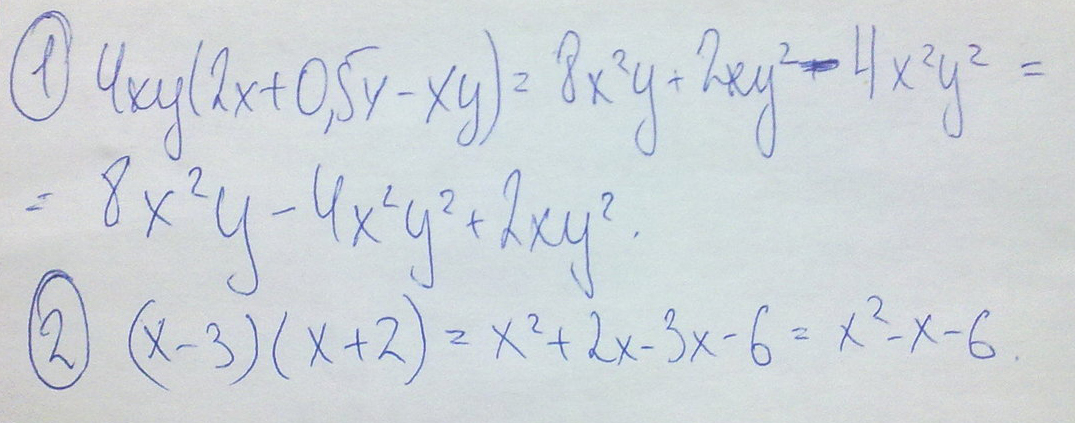
1. Преобразуйте в многочлен:
а) (у
- 4)2; б)
(7х + а)2; в) (5с - 1) (5с + 1); г) (3а + 2b) (3а - 2b).
• 2.
Упростите выражение (а - 9)2
- (81 + 2а).
• 3.
Разложите на множители: а) х2
- 49; б) 25х2 - 10ху +
у2.
4. Решите уравнение (2 - х)2 - х (х
+ 1,5) = 4.
5. Выполните действия: а) (у2 - 2а) (2а + у2); б)
(3х2 + х)2; в) (2 + т)2 (2 - т)2.
6. Разложите на множители: а) 4х2y2 - 9а4;
б) 25а2 - (а + 3)2; в) 27т3 + п3.
Решение: а) (у- 4)2=у в квадрате-8у+16
б)(7x + а)2=49х в квадрате+14ха+а в квадрате
в) (5с - 1) (5с + 1)=25c в квадрате-1
г) (3а + 2b) (3а - 2b)=9а в квадрате-4b в квадрате
Упростите выражение (а - 9)2- (81 + 2а)=2а-18-81-2а=-99
Разложите на множители: а) х2- 49; б) 25х2 - 10ху +у2.
а)(х-7)(х+7) б)(5х-у) в квадрате
5. Выполните действия: а) (у2 - 2а) (2а + у2); б)
(3х2 + х)2; в) (2 + т)2 (2 - т)2.
а) у в квадрате-4а в квадрате
б)9х в 4 степени+6х в кубе+х в квадрате в)(4-т в квадрате)2=16-8т в квадрате+т в 4 степени
1. Преобразуйте в многочлен:
а) (у - 4)2; б) (7х + а)2; в) (5с - 1) (5с + 1); г) (3а + 2b) (3а - 2b).
• 2. Упростите выражение (а - 9)2 - (81 + 2а).
• 3. Разложите на множители: а) х2 - 49; б) 25х2 - 10ху + у2.
4. Решите уравнение (2 - х)2 - х (х + 1,5) = 4.
5. Выполните действия: а) (у2 - 2а) (2а + у2); б) (3х2 + х)2; в) (2 + т)2 (2 - т)2.
6. Разложите на множители: а) 4х2y2 - 9а4; б) 25а2 - (а + 3)2; в) 27т3 + п3.
Решение: А) 2у-8
б) 14х+2а
в) 25с^2 + 5с-5с-1=25с^2 -1
г) 9а^2-5аb+6ab-4b^2=9a^2+ab - 4b^2
2. 2a-18-81-2a= - 63
3.a) =(x-7)(x+7)
б) = (5x-y)^2
4. 4-2x-x^2 -1,5х=4
- x^2-3,5х=0
−x2−3,5x=0
Коэффициенты уравнения:
a=−1, b=−3,5, c=0
Вычислим дискриминант:
D=b2−4ac=(−3,5)2−4·(−1)·0=12,25−0=12,25
(D>0), следовательно это квадратное уравнение имеет 2 различных вещественных корня:
Вычислим корни:
x(1,2)=−b±√D2ax1=−b+√D2a=−(−3,5)+3,52·(−1)=7−2=−3,5x2=−b−√D2a=−(−3,5)−3,52·(−1)=0−2=0
−x2−3,5x=0.5·(x+3,5)x=0Ответ:
x1=−3,5
x2=0
5 а) 2у^2а+у^4 - 4а^2 -2у^2а =у^4- 4 а^2
б) 6х^2+2х