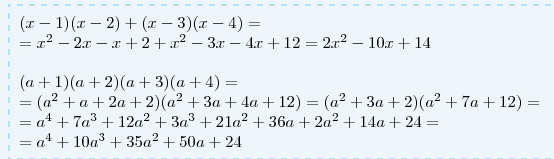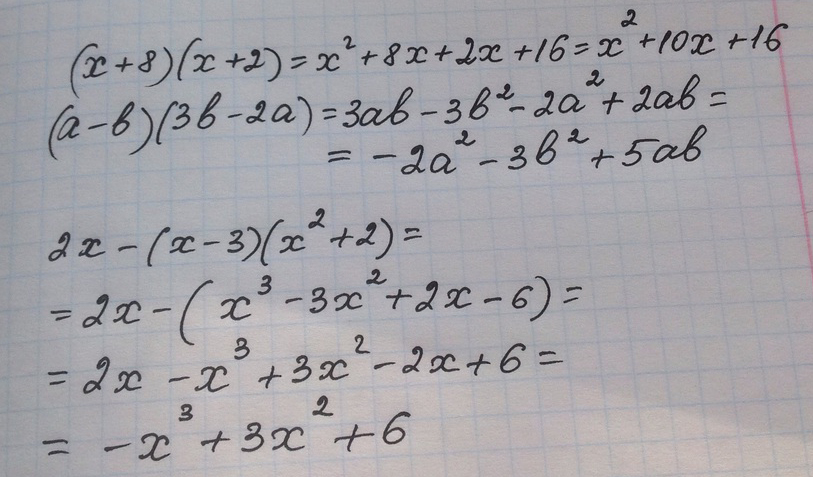многочлен »
представить в виде многочлена - страница 2
Как представить выражение в виде многочлена 1)(х+у) в 3 степини 2)(c-d) в 3 степени 3)(p+g) в 3 степени 4)(p-g) в 3 степени 5)(2+а) в 3 степени 6)(3-g) в 3 степени 7)(х-2) в 3 степени 8) (4+х) в 3 степени 9) (a+2b) в 3 степени
Решение: Применить формулу (а+b)³=a³+3a²b+3ad²+b³
(a-b)³=a³-3a²b+3ab²-b³
(х+у)³=х³+3х²у+3ху²+у³
(с-d)³=c³-3c²d+3cd²+d³
(p+g)³=p³+3p²g+3pg³+g³
(p-g)³=p³-3p²g+3pg²-g³
(2+a)³=8+12a+6a²+a³
(3-g)³=27-27g+9g²-g³
(x-2)³=x³-4x²+12x-8
(4+x)=64+48x+12x²-x³
(a+2b)=a³+6a²b+12ab²+8b³Представить в виде многочлена пж
(а+1)(а+2) (а+3)(а+4)
(х-1)(х-2)+(х-3)(х-4)
Решение: $$ (x-1)(x-2)+(x-3)(x-4)= \\ =x^{2} -2x-x+2+ x^{2} -3x-4x+12=2 x^{2} -10x+14 \\ \\ (a+1)(a+2)(a+3)(a+4)= \\ =(a^2+a+2a+2)(a^2+3a+4a+12)=(a^2+3a+2)(a^2+7a+12)= \\ =a^4+7a^3+12a^2+3a^3+21a^2+36a+2a^2+14a+24= \\ =a^4+10a^3+35a^2+50a+24 $$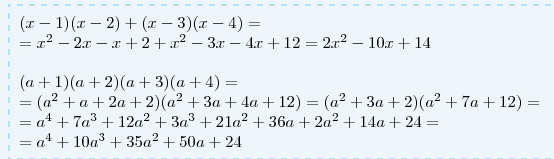
Представить в виде многочлена
(2x-5y+z)^2-(x+3y-z)^2
Решение: $$ (2x-5y+z)^2-(x+3y-z)^2= \\ =[(2x-5y+z)-(x+3y-z)]*[(2x-5y+z)+(x+3y-z)]= \\ =[2x-5y+z-x-3y+z]*[2x-5y+z+x+3y-z]= \\ =[2x-x-5y-3y+z+z]*[2x+x-5y+3y+z-z]= \\ =(x-8y+2z)(3x-2y)= \\ =(x)*(3x)+(x)*(-2y)+(-8y)*(3x)+(-8y)*(-2y)+ \\ +(2z)*(3x)+(2z)*(-2y)= \\ =(+3x^2)+(-2xy)+(-24xy)+(+16y^2)+(+6xz)+(-4yz)= \\ =3x^2-2xy-24xy+16y^2+6xz-4yz= \\ =3x^2+16y^2-26xy+6xz-4yz $$
Представить в виде многочлена выражения : (x+8)(x+2)
(a-b)(3b-2a)
2x-(x-3)(x^2+2)
Решение: 1) x² + 10x + 16
2) 3ab - 2a² - 3b² + 2ab = 5ab - 2a² - 3b²
3) 2x - (x³ + 2x - 3x² - 6) = 2x - x³ - 2x + 3x² + 6 = - x³ + 3x² + 6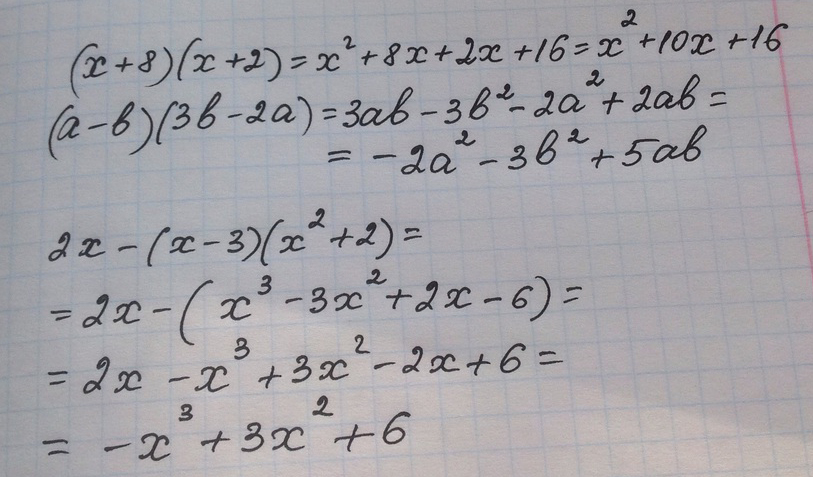
Представить в виде многочленов:
а)(-5а+а)(5+ф)
б)(3х-2у)²
в)(0,1а³-5в)²
г)(х-2)(х²+2х+4)
Решение: а) -25а-5аф+5а+аф=-20а-4афб) 9x²-12xy+4y²
в) 0.01a⁶-а³в+25в²
г) x³+2x²+4x-2x²-4x-8=x³-8
a) первое выражение нужно проверить, чего-то не хватает
в первой скобке нужно упростить
-4а(5+а)=-20а-4а^2
б) квадрат разности
9x^2-12xy+4y^2
в) разность квадратов
0,01a^6-1a^3b+25b^2
г) разность кубов
x^3-8