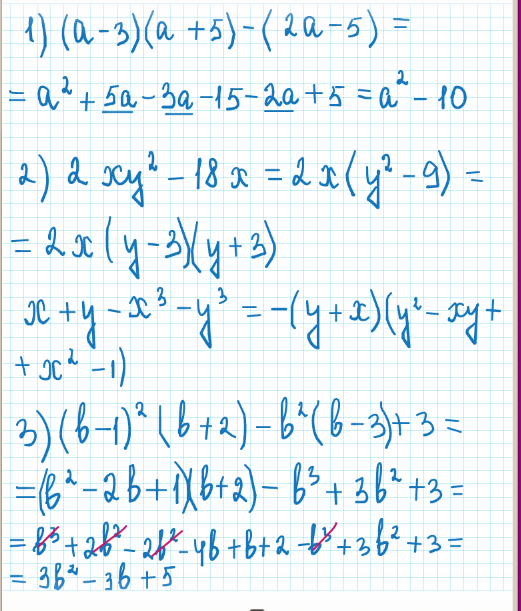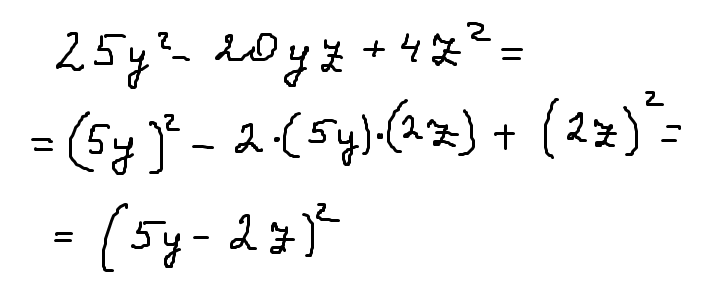многочлен »

представить в виде многочлена - страница 4

  • 1) Упростить.
    (a - 3)(a + 5) - (2a - 5)
    2) Разложить на множители.
    2xy^2 - 18x
    x + y - x^3 - y^3
    3) Представить в виде многочлена.
    (b - 1)^2 (b + 2) - b^2 (b - 3) +3


    Решение: Упростить
    Разложить
    Представить в виде

    1) (a - 3)(a + 5) - (2a - 5)=a^2+5a-3a-15 - 2a + 5=a^2-10
    2)
    2xy^2 - 18x=2x(y^2-9)=2x(y+9)(y-9)
    x + y - x^3 - y^3=x+y-(x^3+y^3)=(x+y)(1-(x^2+y^2))=(x+y)(1-x^2-y^2)
    3)
    (b - 1)^2 (b + 2) - b^2 (b - 3) +3=(b^2-2b+1)(b+2)-b^3+3b^2+3=b^3-2b^2+b+2b^2-4b+2-b^3+3b^2+3=3b^2-3b+5

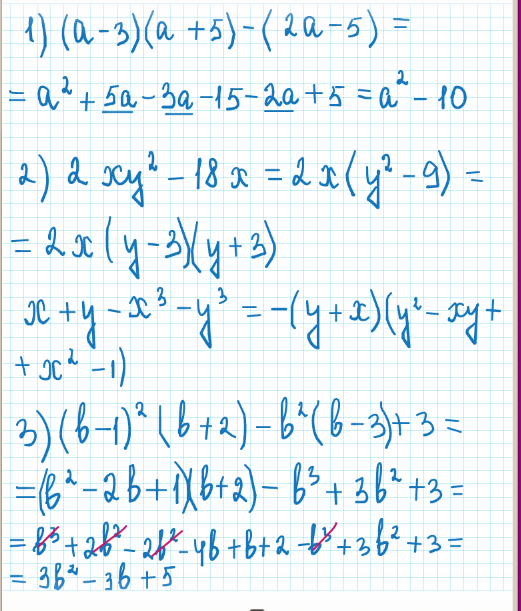
    УпроститьРазложитьПредставить в виде   a - a - a - a a- a- - a a - xy - x x y - x y y- x y - x - y x y- x y x y - x y x y -x -y b - b - b b - b - b b -b b b - b b b - b -b b...

  • Представить квадрат двучлена в виде многочлена:
    (5-p)^2
    (p+6)^2
    (12p^3-5)^2
    (13+6d)^2
    (15k+2)^2
    (11-13a)^2
    (1-b)^2
    (5-6d^5)^2
    (m-5)^2
    (12+d)^2
    (5d+1)^2
    (c^3+4a^2)^2
    (a-1)^2
    (15k^4+13)^2
    (c+7)^2


    Решение: (5-p)²=25-10p+p²
    (p+6)²=p²+12p+36
    (12p³-5)²=144p⁶-120p³+25
    (13+6d)²=169+156d+36d²
    (15k+2)²=225k²+60k+4
    (11-13a)²=121-286a+169a²
    (1-b)²=1-2b+b²
    (5-6d⁵)²=25-60d⁵+36d¹⁰
    (m-5)²=m²-10m+25
    (12+d)²=144+24d+d²
    (5d+1)²=25d²+10d+1
    (c³+4a²)²=c⁶+8c³a²+16a⁴
    (a-1)²=a²-2a+1
    (15k⁴+13)²=225k⁸+390k⁴+169
    (c+7)²=c²+14c+49

    (5-p)^2=25+p^2-10p
    (p+6)^2=p^2+36+12p
    (12p^3-5)^2=144p^6+25-120p^3
    (13+6d)^2=169+36d^2+156d
    (15k+2)^2=255k^2+4+600k
    (1-b)^2=1+b^2-2b

  • Представить квадрат двучлена в виде многочлена.
    1. (n-2)^2
    2. (13-12n^5)^2
    3. (p+6)^2
    4. (p-5)^2
    5. (3-b)^2
    6. (15k^4+13)^2
    7. (8а+3)^2
    8. (9k+14n)^2
    9. (11b+12m)^2
    10. (10a^2-p^4)^2
    11. (1-а)^2
    12.(11-2n^5)^2
    13. (9a+8)^2
    14. (3с+8)^2
    15.(с+3)^2


    Решение: 1) (n-2)^2=n^2-4n+4
    2)(13-12n^5)^2=169-312n^5+144n^10
    3)(p+5)^2=p^2-10p+25
    4)(p+6)^2=p^2+12p+36
    5)(3-b)^2=9-6b+b^2
    6)(15k^4+13)^2=225k^8+390k^4+169
    7)(8a+3)^2=64a^2+48a+8
    8)(9k+14n)^2=81k^2+252kn+196n^2

    n- n - n - n - n n p p - p p p p -b - b b k k k a a a k n k kn n...

  • Представьте многочлен 25y^2-20yz+4z^2 в виде квадрата двучлена.


    Решение: $$ 25y^2-20yz+4z^2=5^2y^2-2\cdot5y\cdot2z+2^2z^2=\\ =(5y)^2-2\cdot5y\cdot2z+(2z)^2=(5y-2z)^2 $$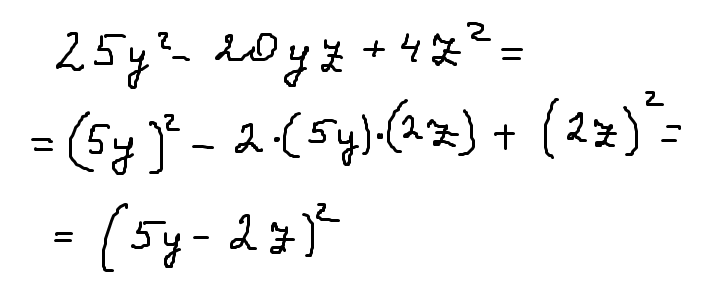

    y - yz z y - cdot y cdot z z y - cdot y cdot z z y- z...

  • Представьте многочлен в виде куба двучлена

    0,125a^9+0,15a^6b^4+0,06a^3b^3+0,008b^12
    0,216x^12-0,54x^8y5+0,45x^4y^10-0,125y^15


    Решение: $$ (x+y)^{3}= x^{3}+3 x^{2} y+ 3xy^{2}+ y^{3} $$ - куб суммы двух чисел (двучлена)
    $$ (x+y)^{3}= x^{3}-3 x^{2} y+ 3xy^{2}- y^{3} $$ - куб разности двух чисел (двучлена)
    Итак, приступим к работе над многочленами:
    $$ 0,125 a^{9}+0,15 a^{6} b^{4}+0,06 a^{3} b^{8}+0,008 b^{12} \\ =(0,5 a^{3})^3+3*0,2(0,5a^{3})^2 b^{4}+3*0,5 a^{3} (0,2b^{4})^2+(0,2 b^{4})^3 \\ = (0,5 a^{3}+0,2 b^{4} )^{3} \\ 0,216 x^{12}-0,54 x^{8} y^{5}+0,45 x^{4} y^{10}+0,125 y^{15} \\ =(0,6 x^{4})^3+3*0,5(0,6x^{4})^2 y^{5}+3*0,6 x^{4} (0,5y^{5})^2+(0,5 y^{5})^3 \\ =(0,6 x^{4}+0,5 y^{5} )^{3} $$
<< < 234 5 > >>