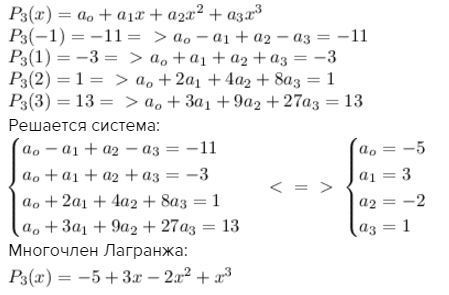многочлен »

задачи с многочленами

  • Докажите, что многочлен не имеет действительных корней: а) x^6-5x^3+7
    б) x^4-x+2


    Решение: То есть, другими словами: нужно найти дискриминант в данных выражениях, приравняв уравнение к нолю.
    а) $$ x^6-5x^3+7 $$
    Делаем замену: x^3=y;
    $$ y^2-5y+7=0; $$
    Находим дискриминант:
    $$ y^2-5y+7=0;\\ D=b^2-4*a*c=25-4*7=25-28=-3; $$
    Т.к. дискриминант получается отрицательным, то уравнение относительно переменной игрек, а значит и икс решений не имеет.
    б) $$ x^4-x+2=0; $$
    Тут увы, сделать замену нельзя. Подумаем логически. Чтобы уравнение имело корень, оно должно занулиться. Перебрасываем 2 в правую часть. смотрим:
    $$ x^4-x+2=0;\\ x^4-x=-2; $$
    Такого по сути быть не может, ибо любое число, пусть даже отрицательное, возведенное в положительную степень будет положительно, и при вычитании никак отрицательного дать не может. Следовательно - уравнение не имеет решений.

  • Найдите свободный член a0a0 многочлена PP с целыми коэффициентами, если известно, что P(19)=P(94)=1994P(19)=P(94)=1994 и что a0a0 по модулю меньше 10001000.


    Решение: Если многочлен 1 степени, то у него не может значение повторяться в двух разных точках.
    Значит, этот многочлен - квадратный.
    P=a2*x^2+a1*x+a0
    Подставляем 19 и 94 вместо х.
    a2*361+a1*19+a0=1994
    a2*8836+a1*94+a0=1994
    Из 2 уравнения вычитаем 1 уравнение
    8475*a2+75*a1=0
    Делим все на 75.
    113*a2+a1=0
    Например, a2=1; a1=-113.
    P=x^2-113x+a0
    Подставляем опять 19
    361-113*19+a0=1994
    a0=1994+113*19-361=3780

  • Поделить многочлен с помощью метода Горнера (6х^6-2х^4+3х^3-х^2+1)/(2х+3)
    ^-степень.


    Решение: запишем в таблицу коэффициенты делимого многочлена(по убыванию степени,3/2 прибавляется к x в делимом)

      |6|0|2|3|-1|0|1

    3/2|

    заполняем

      |6 |0 |2 | 3 | -1 |0 |1

    3/2|6 |

    1)3/2 *6 +0=9

    2)3/2*9+2=31/2

    3)3/2 * 31/2 +3 = 105/4

    4)105/4 * 3/2 -1= 307/8

    5)307/8 * 3/2 +0=921/16

    6)921/16 * 3/2 +1=2795/32

    это и сть каждый следующий столбец твоей таблицы

    и коэффициенты нового уравнения начиная с x^5

  • Используя схему Горнера, докажите, что число a является корнем многочлена p(x)
    p(x)=2x^4-3x^3+x-10 a=2


    Решение: P(x) = 2x^4 - 3x^3 + 0x^2 + x - 10; a = 2
    Выписываем по столбцам коэффициенты уравнения,
    а в строку пишем корень а = 2.
    p | 2 | -3 | 0 | 1 | -10
    -
    2 | 2 |  1 | 2 |  5 | 0
    Старший член просто переписываем - 2.
    Дальше умножаем его на корень 2 и прибавляем следующий (-3).
    Получили 1, который пишем под -3.
    Опять умножаем эту 1 на корень 2 и прибавляем коэффициент 0.
    Получили 2, пишем его под 0.
    Умножаем эту 2 на корень 2 и прибавляем коэффициент 1.
    Получили 5, записываем под 1.
    И, наконец, умножаем эту 5 на корень 2 и прибавляем -10.
    В конце получился 0, значит, 2 - это корень.

  • X³ + 2/3*X² - 1/9 =0 ( 10 класс, многочлены) решить нужно либо по теореме Безу, либо по схеме Горнера.


    Решение: X³+(2/3)x²-1/9
    x₁=1/3
    x³+(2/3)x²-1/9   |_x-1/3_
    x²-1/3x²            | x²+x+1/3
    -
             x²-1/9
             x²-(1/3)x
            -
                    (1/3)x-1/9
                    (1/3)x-1/9
                    -
                                  0
    x²+x+1/3=0   D=-4¹/₃ ⇒ Уравнение не имеет действительных корней.
    Ответ: x=1/3.

  • Найдите многочлен М и вычислите его значение при х= -1, если М · (х + 2)= х^3 + 2х^2 + 2х + 4


    Решение: М · (х + 2)= х^3 + 2х^2 + 2х + 4
    чтобы получить M, нужно многочлен х^3 + 2х^2 + 2х + 4 разделить на x+2
     х^3 + 2х^2 + 2х + 4 | x+2
    x^3 + 2x^2 x^2 + 2
      2x +4
      2x+4
    0
    Значит M(x)=x^2+2
    M(-1) = (-1)^2 +2 =3

    Оууу тут так легко, просто подставляете в место "x" "-1"
    и находите "M" как простое уравнение:
    М(х + 2) = х³ + 2х² + 2х + 4
    М(-1 + 2) = (-1)³ + 2*(-1)² + 2*(-1) + 4
    M = -1 + 2 - 2 + 4
    М = 1

  • Найти многочлен M(x) третьей степени такой, что M(-1)=-2, M(0)=1, M(1)=0, M(2)=1


    Решение: $$ M(x)=ax^3+bx^2+cx+d\\M(0)=1\\d=1\\M(-1)=-a+b-c=-2\\M(1)=a+b+c=0\\M(2)=8a+4b+2c=1 $$
    Решаем получившуюся систему:
    $$ -a+b-c=-2\\a+b+c=0\\8a+4b+2c=1 $$
    Получаем:
    $$ a=\cfrac{1}{2};\phantom{g} b=-1;\phantom{g} c = \cfrac{1}{2} $$
    Получаем многочлен:
    $$ M(x)=\cfrac{1}{2}\cdot x^3-x^2+\cfrac{1}{2}\cdot x+1 $$

    (2 фото), на одном не уместилось

    M x ax bx cx d M d M - -a b-c - M a b c M a b c Решаем получившуюся систему -a b-c - a b c a b c Получаем a cfrac phantom g b - phantom g c cfrac Получаем многочлен M x cfrac...

  • Найти интерполяционный многочлен Лагранжа P3(x), для которого P3(-1)=-11, P3(1)=-3, P3(3)=13.


    Решение: $$ P_3(x)=a_o+a_1x+a_2x^2+a_3x^3\\ P_3(-1)=-11=\ > \ a_o-a_1+a_2-a_3=-11\\ P_3(1)=-3=\ > \ a_o+a_1+a_2+a_3=-3\\ P_3(2)=1=\ > \ a_o+2a_1+4a_2+8a_3=1\\ P_3(3)=13=\ > \ a_o+3a_1+9a_2+27a_3=13 $$
    Решается система:
    $$ \begin{cases} a_o-a_1+a_2-a_3=-11 \\a_o+a_1+a_2+a_3=-3\\ a_o+2a_1+4a_2+8a_3=1 \\ a_o+3a_1+9a_2+27a_3=13 \end{cases} \ < \ =\ > \ \begin{cases} a_o =-5 \\ a_1=3\\ a_2=-2 \\ a_3=1 \end{cases} $$
    Многочлен Лагранжа:
    $$ P_3(x)=-5+3x-2x^2+x^3 $$

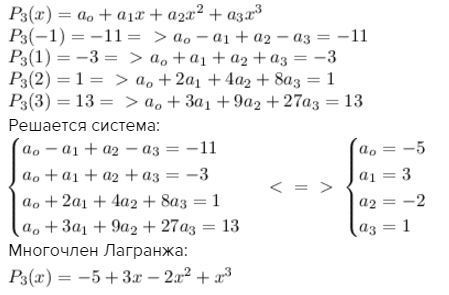
    P x a o a x a x a x P - - a o-a a -a - P - a o a a a - P a o a a a P a o a a a Решается система begin cases a o-a a -a - a o a a a - a o a a a a o a a a end cases begin cases...

  • Решите уравнения:
    а)2x+8x^2=0
    б)x^2-x=2x-5
    в)x^4-3x^2-4=0
    Разложите если возможно, на множители многочлена
    x^2-2x-15


    Решение: $$ a) 2x+8x^2=0;\\x(2+8x)=0;\\ \left [ {{x_1=0;} \atop {2+8x=0;}} \right. \\\left [ {{x_1=0;} \atop {8x=-2;}} \right. \\\left [ {{x_1=0;} \atop {x_2=- \frac{1}{4}; }} \right. $$
    Ответ: $$ -\frac{1}{4}; 0. \\ b)x^2-x=2x-5;\\x^2-x-2x+5=0;\\x^2-3x+5=0;\\D=9-4*1*5=9-20<0 => x \in \emptyset. $$
    Ответ: $$ x \in \emptyset. \\ x^4-3x^2-4=0;\\(x^2)^2-3x^2-4=0;\\ t=x^2;\\t^2-3t-4=0;\\D=9+16=25;\\t_1= \frac{3+5}{2}=4;\\t_2= \frac{3-5}{2}=-1;\\ \left [ {{x^2=4;} \atop {x^2=-1; }} \right.\\ \left \{ {{x_1=2;x_2=-2;} \atop {x \in \emptyset;}} \right. $$
    Ответ: -2;2.
    $$ ax^2+bx+c=a(x-x_1)(x-x_2) \\ x^2-2x-15=0; \\D=4+60=64;\\x_1= \frac{2+8}{2}=5;\\x_2= \frac{2-8}{2}=-3;\\ x^2-2x-15=1*(x-5)(x-(-3))=(x-5)(x+3);\\ x^2-2x-15=(x-5)(x-3). $$

    $$ \mathsf{2x+8x^{2}=0}\\ \mathsf{x(8x+2)=0}\\ \mathsf{x=0}\\ \mathsf{8x+2=0 \longrightarrow 8x=-2 \longrightarrow x=- \frac{1}{4}} $$
    Ответ: 0; $$ - \frac{1}{4} $$.
    $$ \mathsf{x^{2}-x=2x-5}\\ \mathsf{x^{2}-3x+5=0}\\ \mathsf{D=9-4\times1\times5<0} \longrightarrow \varnothing $$
    Ответ: нет корней.
    $$ \mathsf{x^{4}-3x^{2}-4=0}\\ \mathsf{x^{2}=t}\\ \mathsf{t^{2}-3t-4=0}\\ \mathsf{t_{1}=4}\\ \mathsf{t_{2}=-1}\\ \mathsf{x^{2}=4 \longrightarrow x=\pm2}\\ \mathsf{x^{2}=-1 \longrightarrow \varnothing} $$
    Ответ: $$ \pm 2 $$.

  • Определите многочлен А и найдите его степень, используя правила нахождения неизвестного слагаемого, уменьшаемого и вычитаемого.
    а) А+(12у^2+6y-1)=-10+9
    б) (-6x^2+7x-11)-A=2x^2+2x-1
    в) A-(6a^2_5ab+b^3)=4b^3-11ab
    г) (25x^5-13x^3+7)+A=15x^5-13x^2


    Решение: а) А + (12у² + 6y - 1) = -10 + 9
    А = -10 + 9 - (12y²+6y-1)
    A = -1 - 12y² - 6y + 1
    A = -12y² - 6y
    б) (-6x² + 7x - 11) - A = 2x² + 2x - 1
    A = -6x² + 7x - 11 - 2x² - 2x + 1
    A = -8x² + 5x - 10
    в)  A - (6a² - 5ab + b³) = 4b³ - 11ab
    A - 6a² + 5ab - b³ = 4b³ - 11ab
    A = 4b³ - 11ab + 6a² - 5ab + b³
    A = 5b³ + 6a² -16ab
    г) (25x⁵ - 13x³ + 7) + A = 15x⁵ - 13x²
    A = 15x⁵ - 13x² - 25x⁵ + 13x³ - 7
    A = -10x³ - 7

1 2 3 > >>