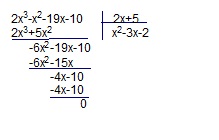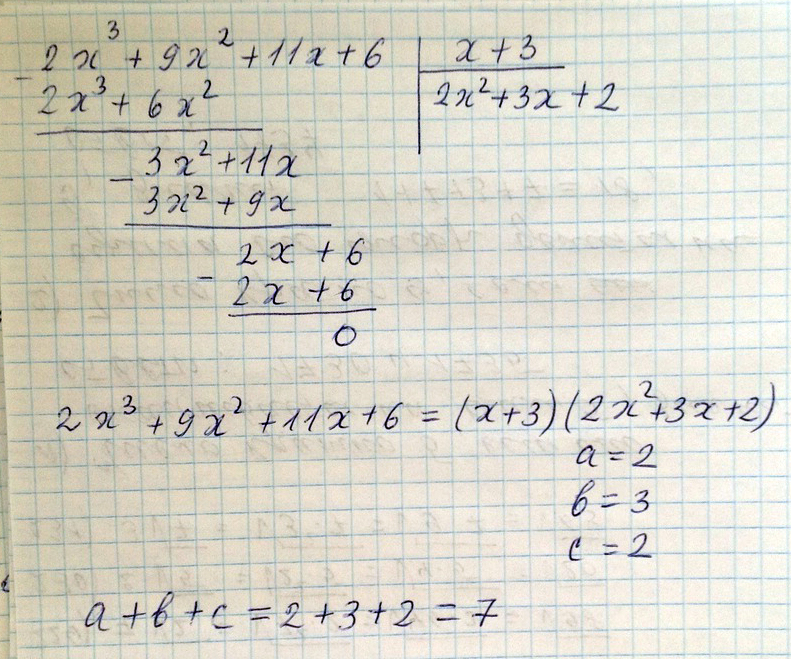многочлен »

задачи с многочленами - страница 4

  • Если многочлен 2x^3+9x^2-9x+2 можно представить в виде (2x-1)(ax^2+bx+c), то сумма a+b+c равна?


    Решение: $$ 2x^3+9x^2-9x+2=2x^3-x^2+10x^2-5x-4x+2=\\\\x^2(2x-1)+5x(2x-1)-2(2x-1)=\\\\(2x-1)(x^2+5x-2) $$
    -
    $$ a+b+c=1+5+(-2)=4 $$
    -
    ответ: 4
    -
    второй способ: из условия ясно что один из корней равен 2х-1=0; 2х=1; х=0.5
    используем теорему Виета для кубического уравнения
    $$ x_1+x_2+x_3=-\frac{9}{2} \\ x_1x_2+x_2x_3+x_1x_3=\frac{-9}{2} \\ x_1x_2x_3=-\frac{2}{2}=-1 $$
    учитывая что $$ x_3=0.5 $$
    легко увидеть что
    $$ x_1+x_2=-5 \\ x_1x_2=-2 $$
    дальше
    учитывая что
    $$ a_1x^3+a_2x^2+a_3x+a_4=a_1(x-x_1)(x-x_2)(x-x_3)=\\\\a_1(x-0.5)(x^2-(x_1+x_2)x+x_1x_2)) \\ 2x^2+9x-9x+2=2(x-0.5)(x^2+5x-2)=\\\\(2x-1)(x^2+5x-2)=(2x-1)(ax^2+bx+c) $$
    то $$ a+b+c=1+5+(-2)=4 $$
    ответ: 4

    $$ (2x-1)(a x^{2} +bx+c)=2x ^{3} +9 x^{2} -9x+2 $$
    Раскроем скобки в левой части:
    $$ 2ax ^{3} -a x^{2}+2b x^{2} -bx+2cx-c=2 x^{3} +9 x^{2} -9x+2 \\ 2a x^{3} +(2b-a) x^{2} +(2c-b)x-c=2 x^{3} +9 x^{2} -9x+2 $$
    Два многочлена равны тогда и только тогда когда их степени равны и равны коэффициенты при соответствующих степенях переменной:
    $$ 2a=2, a=1, \\ (2b-a)=9,2b-1=9,2b=10,b=5, \\ 2c-b=-9,2c-5=-9,2c=-4, c=-2, \\ -c=2, c=-2 $$
    Ответ a+b+c=1+5-2=4

  • Если многочлен 2х(в кубе)-х(в квадрате)-19х-10 можно представить в виде (2х+5)(ах[в квадрате]+вх+с), то сумма а+в+с равна?


    Решение: (2x^3-x^2-19x-10)/(2x+5)=x^2-3x-2 с методом разделение многочлена на многочлена

    a=1,b=-3,c=-2

    a+b+c=-4

    проверка

    (2х^3-x^2-19x-10)=(2x+5)(x^2-3x-2)

    ax^2+bx+c=x^2-3x-2. Отсюда: a=1, b=-3, c=-2. Значит, a+b+c=1-3-2=-4

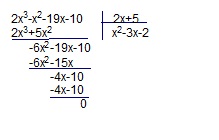
    x -x - x- x x - x- с методом разделение многочлена на многочлена a b - c - a b c - проверка х -x - x- x x - x- ax bx c x - x- . Отсюда a b - c - . Значит a b c - - -...

  • Если многочлен 2x^3+9x^2+11x+6 можно представить в виде (x+3)(ax^2+bx+c), то сумма a+b+c =?


    Решение: Делим в столбик на (x+3)

    получаем 2x^2+3x+2

    многочлен принял вид (x+3)(2x^2+3x+2)

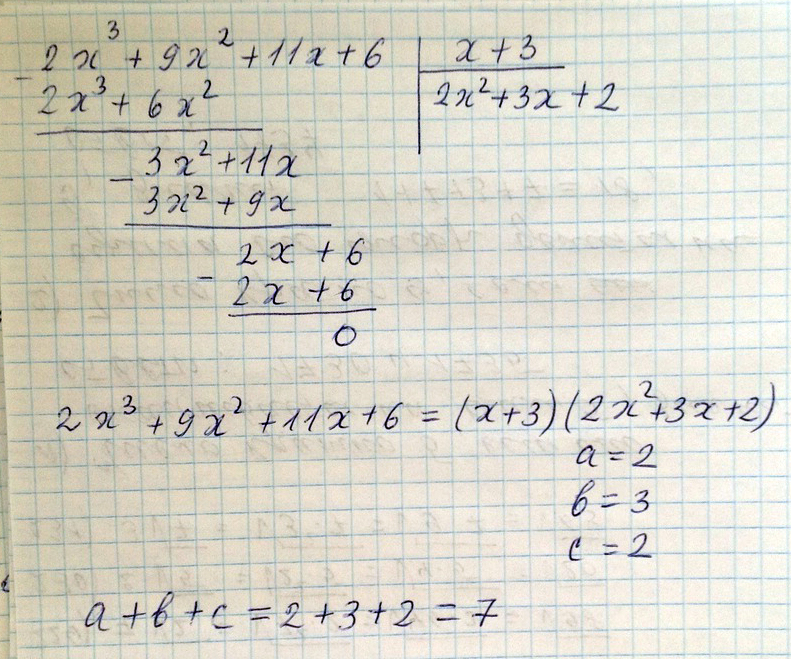
    a+b+c=2+3+2=7Делим в столбик на x получаем x x многочлен принял вид x x x a b c...

  • Если многочлен
    2х^3+9х^2-9х+2 можно представить в виде (2х-1)(aх^2+вх+с), то сумма а+в+с равна?


    Решение: Чтобы узнать значение а, в и с, можно поделить многочлен на (2х-1) столбиком.

    2х³+9х²-9х+2I2х-1

    2х³-х²            |х²+5х-2

         10х²-9х

         10х²-5х

                -4х+2

                -4х+2

                       0

    Получили многочлен х²+5х-2, значит, а=1, в=5, с=-2

    Их сумма равна 1+5-2=4

    Ответ:4

  • 1) Используя ф-лы сокр. умн. (3x-2)^3-(2x+1)^3=0 2) Методом выделения полного квадрата x^4-7x^2+12=0 3) Способом группировки 2x^4+3x^3-8x^2-12x=0 4) Путем подбора корня многочлена по его старшему и свободному коэффициентам x^3-6x^2+5x+12=0 5) Методом введения параметра x^3-(/2/+1)x^2+2=0 /2/ - в смысле корень из двух


    Решение: (3x-2)^3-(2x+1)^3=0

    (3x-2-2x-1)((3x-2)^2+(3x-2)(2x+1)+(2x+1)^2)=0

    (x-3)(9x^2-12x+4+6x^2-x-2+4x^2+4x+1)=0

    (x-3)(19x^2-9x+3)=0

    x=3 второе ур через дискриминант’

    2) Методом выделения полного квадрата x^4-7x^2+12=0

    (x^2)^2-2*x^2*3.5+3.5^2-3.5^2+12=0

    (x^2-3.5)^2=12.25-12=0.25

    x^2-3.5=-0.5 x^2=3 x1=-V3 x2=V3

    x^2-3.5=0.5 x^2=4 x3=-2 x4=2

    3) Способом группировки 2x^4+3x^3-8x^2-12x=0

    2x^2(x^2-4)+3x(x^2-4)=0

    (x^2-4)(2x^2+3x)=0

    (x-2)(x+2)x(2x+3)=0

    x=2 x=-2 x=0 x=-1.5

<< < 234 5 6 > >>