логарифм »
логарифмическое уравнение
Срочно решите логарифмические уравнения: a)\( \log_2(x-4)=3\); b) \(\log_2x + \log_2(x-3)=2 \)
Решение:
а) (х-4)=9, х = 13
б) log х * (х-3) = 2
log х^2 - 3x = 2
х^2 - 3x = 1
х^2 - 3x -1=0
$$ log_{2} (x-4)= 3 \\ log_{2} (x-4)= log_{2} 2^{3} \\ (x-4)= 2^{3} \\ x-4= 8 \\ x= 8+4 \\ x= 12 \\ log_{2} x + log_{2} ( x-3) = 2 \\ log_{2}( x*( x-3)) = log_{2} 2^{2} \\ x*( x-3) = 2^{2} \\ x^{2} -3x = 4 \\ x^{2} -3x - 4=0 $$
Подбором по формулам Виета
$$ x_{1} =4 \\ x_{2} =-1 $$
Решить логарифмические уравнения:
1) log2(x-5)-log2(2x+5)=3log2 2
2)lg^(2)x-lgx-6=0 (подстановка log2x=y)
3)2^x+2^(x-2)+2^(x-3)=11\\4 <-(дробь)
4)9*3^2x-28*3^x+3=0 (подстановка 3^x=y)
Решение: 1. log2(x-5)\(2x+5)=log2 8
(x-5)\2x+5)=8
x-5=16x+40
15x=-45
x=-3
2. lgx=t
t^2-t-6=0 t1=3, t2=-2
lgx=3 lgx=-2
x1=1000 x2=0,01
3. 2^x+(2^x)\4+(2^x)\8=11\4 умножаем все уравнение на 8 и подставляем вместо 2^x=t
8t+2t+t=22
11t=22
t=2
2^x=2
x=1
4. 9y^2-28y+3=0
y1=1\9 3^x=1\9
x1=-2
y2=3 3^x=3
x2=1Решить логарифмические уравнения: 4) \(\log_{27}(3x^2+4x-4)=\frac{1}{3}\)
5) \( \log_5 x - \lg x = \log_{100} 16 \)
Решение: 4) log₂₇(3x²+4x-4)=1/3
одз:3x²+4x-4>0
3x²+4x-4=0
x1=-2 x2=2/3
+ - +
//////////////////////////(-2)-(2/3)//////////////////////////
x∈(-∞;-2)∪(2/3;-∞)
log₂₇(3x²+4x-4)=log₂₇(27^(1/3))
(3x²+4x-4)=3
3x²+4x-7=0
D=16-4·3(-7)=16+84=100
x1=(-4-10)/6=-7/3 ∈ (-∞;-2)∪(2/3;-∞)
x2=(-4+10)/6=1 ∈ (-∞;-2)∪(2/3;-∞)
5) log₅x-lgx=log₁₀₀16
одз: x>0
(lgx)/lg5=(lg16)/2
lgx=lg5·(lg16)/2
lgx=lg5·(lg4)
x=5^(lg4)Решить логарифмические уравнения : 1) \(\log_{\frac{1}{2}}(3x-1)=\log_{\frac{1}{2}}(6x+8) \)
2) \(\log_2(3x+1) \log_3 x=\log_3 x \)
3) \( \log_3(x-2)+\log_3(x+6)=2 \)
4) \(\lg(3x-1)-\lg(x+5)=\lg5 \)
5) \( \log_3^2x+7\log_3 x +10 =0 \)
Решение: 1.3x-1=6x+8, 3x-6x=8+1,3x=9, x=9/(-3)=-3
При х=-3 log₀,₅(3x-1) не имеет смысла.
Ответ: нет корней
2.log₂(3x+1)·log₂x-log₂x=0, log₂x ( log₂(3x+1)-1)=0, log₂x=0, x₁=2⁰=1
log₂(3x+1)-1=0, log₂(3x+1)=1, 3x+1=2¹, 3x+1=2, 3x=2-1, 3x=1, x₂=1/3.
3.(x-2)(x+6)=3², x²+4x-12-9=0, x²+4x-21=0, D=16-4*(-21)=16+84=100
√D=10, x₁=(-4+10)/2=3, x₂=(-4-10)/2=-7 не является корнем, т. к. при х=-7
log₃(x+6) не имеет смысла, как log₃(x-2)
Ответ: х=3
4. (3х-1)/(х+5)=5, 3х-1=5(х-5), 3х-1=5х+25, 3х-5х=25+1,2х=26, х= -13-не подходит по смыслу.
Ответ: нет корней
5. По определению логарифма имеем: х²-7=2, х²=9, х₁=-3, х₂=3
Ответ: -3 и 3
Решите логарифмические уравнения: 1) \(\log_3 x=2-\log_{\frac{1}{3}}2 \)
2) \(\log_{\frac{1}{2}}x -\log_2 x =2\)
3) \( 3\cdot\log_5^2 x +\log_5 x=4 \)
4) \(\log_3 \log_2(x+3) =1 \)
5) \(\log_{\frac{1}{2}}x +\log_{\frac{1}{2}}(x+1)=1 \)
Решение: 1
x>0
log(3)x=2+log(3)2
log(3)x=log(3)18
x=18
2
x>0
-log(2)x-log(2)x=2
-2log(20x=2
log(20x=-1
x=0,5
3
x>0
log(5)x=a
3a²+a-4=0
D=1+48=49
a1=(-1-7)/6=-4/3⇒log(5)x=-4/3⇒1/5∛5
a2=(-1+7)/6=1⇒log(50x=1⇒x=5
4
x>-3
log(3)log(2)(x+3)=1
log(2)(x+3)=3
x+3=8
x=5
5
x>-1
log(1/2)(x²+x)=1
x²+x=0,5
2x²+2x-1=0
D=4+8=12
x1=(-2-2√3)/4=-0,5(1+√3) не удов усл
x2=0,5(√3-1)

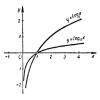 Логарифмической функцией называется функция вида
y = logax,
где а - некоторое фиксированное положительное число, отличное от 1.
Формула y = logax выражает то же самое, что и формула
аy= х. (1)
Отсюда легко установить связь между логарифмической функцией и показательной функцией
у = аx (2)
Если показательная функция (2) описывает изменение степени в зависимости от изменения ее показателя, то ввиду (1) логарифмическая функция, наоборот, описывает изменение...
Логарифмической функцией называется функция вида
y = logax,
где а - некоторое фиксированное положительное число, отличное от 1.
Формула y = logax выражает то же самое, что и формула
аy= х. (1)
Отсюда легко установить связь между логарифмической функцией и показательной функцией
у = аx (2)
Если показательная функция (2) описывает изменение степени в зависимости от изменения ее показателя, то ввиду (1) логарифмическая функция, наоборот, описывает изменение...