логарифмическое уравнение - страница 3
Решите логарифмические уравнения: 1) \( x^{\log_3x-2}=27 \)
2) \( x^{\log_2x-3}=16 \)
3) \( x^{3-\log_3x}=9 \)
4) \( x^{\log_5x+2}=125 \)
Решение: 1/ Так как x=3^(log3_x); (3^log3_x)^log3_x=3^3; 3^((log3_x)^2-2*log3_x)=3^3; (log3_x)^2-2*log3_x=3; log3_x=t; t^2-2t-3=0; D=4+12=16=4^2; t1=-1; log3_x=-1; x1=3^(-1)=1/3; t2=3; log3_x=3; x2=3^3=27. ответ : х= 1/3. х=27. 2) так как х=2^(log2_x); 2^(log2_x)^2-3*log2_x)=16=2^4; (log2_x)^2-3*log2_x=4; log2_x=t; t^2-3t-4=0; t1=-1; log2_x=-1; x1=2^-1=1/2; t2=4; log2_x=4; x2=2^4=16. 3) так как x=3^(log3_x), следует 3^(3*log3_x-(log3_x)^2)=3^2; 3*log3_x-(log3_x)^2=2; log3_x=t; 3t^2-t-2=0; t1=1; log3_x=1; x=3^1=3; t2=-2/3; log3_x=-2/3; x=3^(-2/3). 4. x=5^(log5_x); 5^((log5_x)^2+2*log5_x)=5^3; (log5_x)^2+2*log5_x=3; log5_x=t; 5^2+2t-3=0; t1=-1; log5_x=-1; x1=5^-1=1/5; t2=3; log5_x=3; x2=5^3=125Найдите значение выражения \( \log_{0,15}20 - \log_{0,15}3 \)
Решение: log₀.₁₅20-log₀.₁₅3=log₀.₁₅(20/3)=log₀.₁₅(3/20)⁻¹=-1log₀.₆10-log₀.₆6=log₀.₆(10/6)=log₀.₆(6/10)⁻¹=-1
Используется формула:
есть формула логарифма дроби по основанию а - логарифм числителя по осн а минус логарифм знаменателя по осн а
здесь обратная ей, т е 2 выражение равно log по осн 0.6 числа 10/6
далее 10/6 представляем как 6/10^-1, т е ( 0.6)
-1 выносим перед логарифмом, log числа 0.6 по осн 0.6 равен 1
-1*1=-1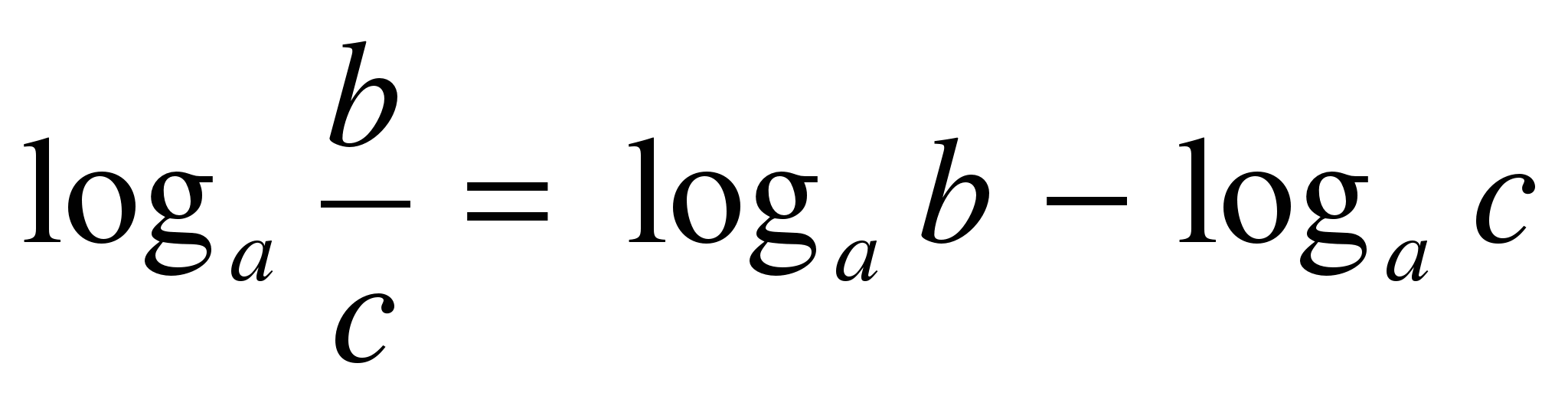
решить логарифмические уравнения. 1) \( \log_3(2x+1)=2 \)
3) \(\lg_(6x+7)=\lg(4x+1) \)
5) \(\log_{0,7}x +\log_{0,7}(x+1)=\log_{0,7}2 \)
Решение: 1
ОДЗ
2x+1>0⇒x>-0,5
2x+1=9
2x=8
x=4
3
ОДЗ
2-5x>0⇒5x<2⇒x<0,4
2-5x=8
2x=-6
x=-1,2
5
ОДЗ
{x>0
{x+1>0⇒x>-1
x∈(0;∞)
log(0,7)(x²+x)=log(0,7)2
x²+x=2
x²+x-2=0
x1+x2=-1 U x1*x2=-2
x1=-2∉ОДЗ
x2=1
1) Log_3 (2x+1) =2 ⇔ 2x+1 = 3² ⇒ x = 4.
-
3) Lg(6x+7) = Lq (4x+1) ⇔{ 6x+7>0 ; 4x+1>0 ; 6x+7 = 4x +1 ⇔{ x> -1/4 ; x = -3⇒
x ∈ ∅.
-
5) Loq _(0,7) x +Log_(0,7) (x+1) = Lq_(0,7) 2 ⇔{ x>0 ; x +1>0 ; x(x+1) =2⇔
{ x>0 ; x² + x -2 =0 ⇔ { x>0 ; [ x = -2 ; x =1.⇒ x =1.
Найдите произведение корней уравнения \(\log_x2 + log_{4x}4 = 1\)
Решение: $$ 1) \log_x2 + log_{4x}4 = 1\\\\ 1/log_2x + 2/log_24x = 1\\\\ log_24x + 2log_2x = log_24xlog_2x\\\\ log_24x + 2log_2x - log_24xlog_2x = 0\\\\ log_24x(1 - \log_2x)+2log_2x = 0\\\\ (log_24+log_2x)(1 - log_2x) + 2log_2x = 0\\\\ (2+log_2x)(1 - log_2x) + 2log_2x = 0\\\\ 2 - log^2_2x - log_2x + 2log_2x = 0\\\\ -log^2_2x + log_2x + 2 = 0 log_2x = t\\\\ -t^2+t+2 = 0\\\\ t = -1, t = 2\\\\ log_2x = -1, x = 1/2\\\\ log_2x = 2, x = 4\\\\ x_1*x_2 = 2\\\\ $$Как решаются логарифмические уравнения подобного вида? \(\log_{\frac{1}{3}}^2 +7\log_{\frac{1}{3}}+12=0 \)
Решение: ОДЗ: x>0
Сделаем замену: пусть log2/3(x)=t, тогда:
t^2+7t+12=0
D=7^2-4*12=1
t1=(-7-1)/2=-4
t2=(-7+1)/2=-3
Сделаем обратную замену:
1).log2/3(x)= -4
2).log2/3(x)=-3
Решим эти два уравнения:
1)log2/3(x)=-4
log2/3(x)=log2/3 (81/16)
x=81/16 = 5 1/16
2). log2/3(x)=-3
log2/3(x)=log2/3(27/8)
x=27/8=3 3/8
Вводите новую переменную: log2/3x = t
Тогда уравнение такое:
t^2 + 7t + 12 = 0
D = 49-48 = 1
t1 = (-7-1)/2 = -4
t2 = (-7+1)/2 = -3
Теперь вместо t подставляете:
log2/3x = -4
x = (2/3)^-4 = (3/2)^4 = 81/16 = 5 целых 1/16
log2/3x = -3
х = (2/3)^-3 = (3/2)^3 = 27/8 = 3 целых 3/8
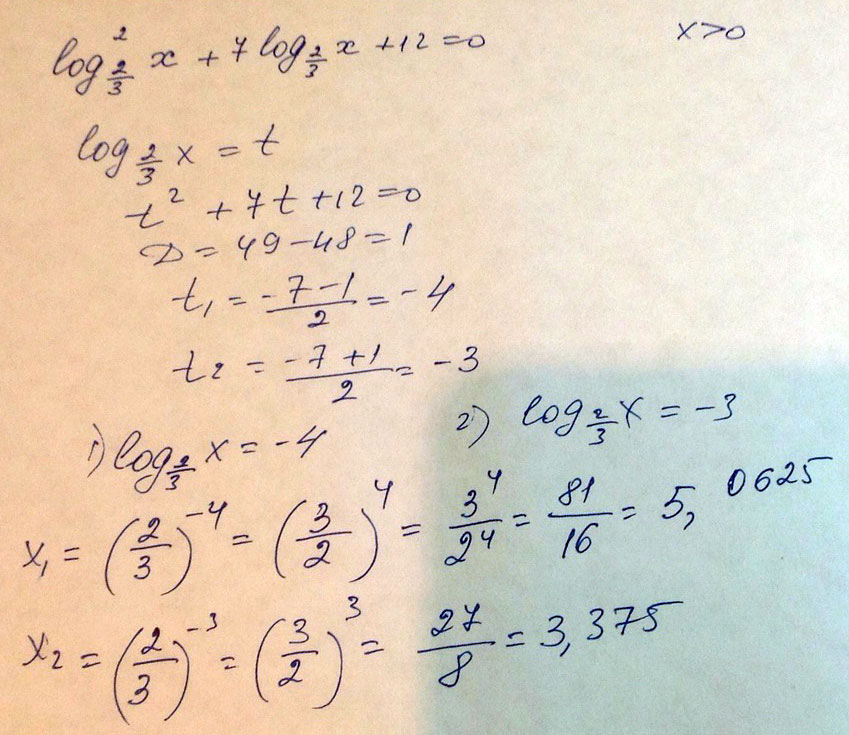

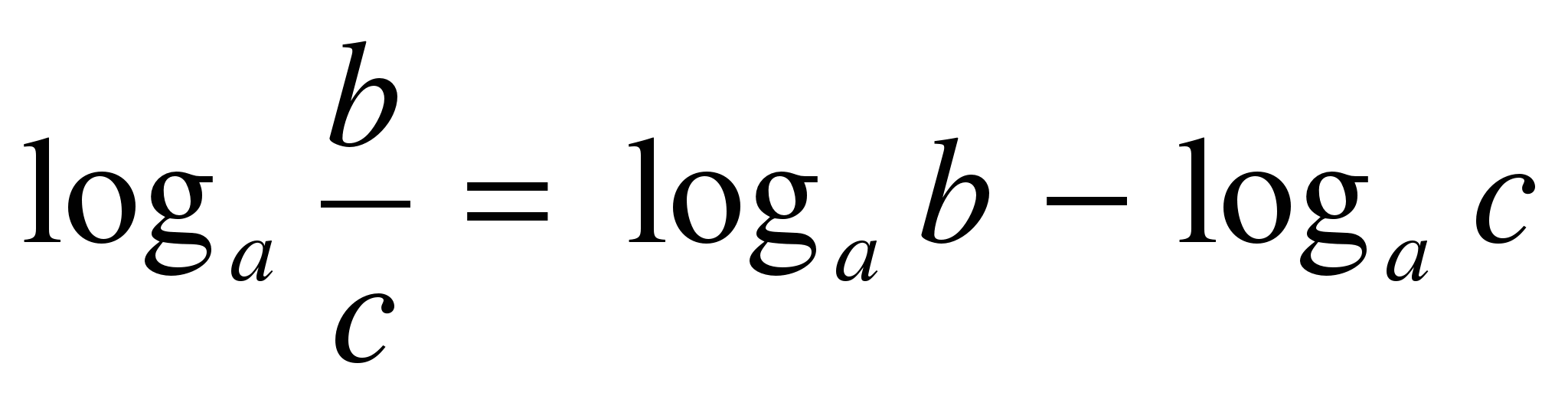
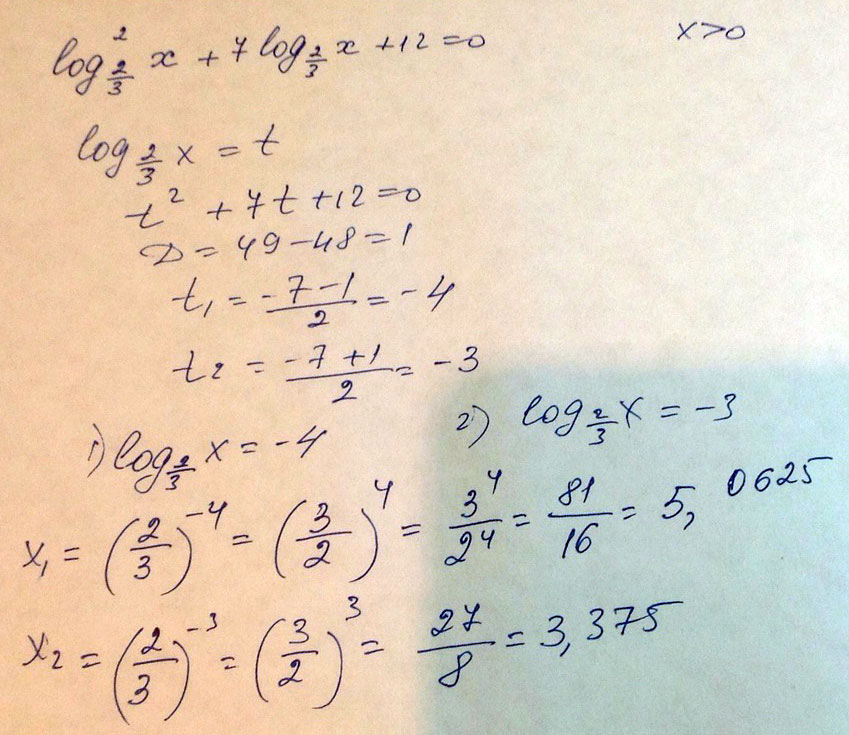
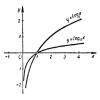 Логарифмической функцией называется функция вида
y = logax,
где а - некоторое фиксированное положительное число, отличное от 1.
Формула y = logax выражает то же самое, что и формула
аy= х. (1)
Отсюда легко установить связь между логарифмической функцией и показательной функцией
у = аx (2)
Если показательная функция (2) описывает изменение степени в зависимости от изменения ее показателя, то ввиду (1) логарифмическая функция, наоборот, описывает изменение...
Логарифмической функцией называется функция вида
y = logax,
где а - некоторое фиксированное положительное число, отличное от 1.
Формула y = logax выражает то же самое, что и формула
аy= х. (1)
Отсюда легко установить связь между логарифмической функцией и показательной функцией
у = аx (2)
Если показательная функция (2) описывает изменение степени в зависимости от изменения ее показателя, то ввиду (1) логарифмическая функция, наоборот, описывает изменение...