логарифм »
логарифмическое уравнение - страница 5
Решить логарифмические уравнения \(log_{7}(x-1)*log_{7}x=log_{7}x \);
\(\frac{1}{2}lg(x^2+x-5)=lg5x+lg \frac{1}{5x}\)
Решение: 1.
$$ log_{7}(x-1)*log_{7}x=log_{7}x \\ \\ x\ > \ 0 \\ x-1\ > \ 0 \\ x\ > \ 1 \\ log_{7}(x-1)= \frac{log_{7}x}{log_{7}x} \\ log_{7}(x-1)=1 \\ x-1 =7^1 \\ [tex]x=8 $$ $$ \\ $$
Ответ: 8
2.
$$ \frac{1}{2}lg(x^2+x-5)=lg5x+lg \frac{1}{5x} \\ \\ $$
ОДЗ:
1) x²+x-5>0
2) 5x>0
3) $$ \frac{1}{5x}\ > \ 0 \\ lg(x^2+x-5)^{ \frac{1}{2} }=lg(5x* \frac{1}{5x} ) \\ lg \sqrt{x^2+x-5}=lg 1 \\ \sqrt{x^2+x-5} =1 \\ x^2+x-5=1 \\ x^2+x-5-1=0 \\ x^2+x-6=0 \\ D=1+24=25 \\ x_{1}= \frac{-1-5}{2}=-3 \\ x_{2}= \frac{-1+5}{2}=2 $$
Проверка корней по ОДЗ:
х=-3
1) (-3)² -3-5>0
1>0 - верно
2) 5*(-3)>0
-15>0 - не верно
х= -3 - не подходит
х=2
1) 2² +2-5>0
1>0 - верно
2) 5*2>0
10>0 - верно
3) 1/(5*2)>0
0.1>0 - верно
х=2 - подходит
Ответ: 2.Логарифмические уравнения
log_0.2 ( x^3+5x^2+6x+1) = log_0.2 (-x^3+2x^2+3x)
Решение: ОДЗ:$$ \left \{ {{x^3+5x^2+6x+1>0} \atop {-x^3+2x^2+3x>0}} \right. $$
Решать не будем, так как сложная система
Решим уравнение и сделаем проверку.
$$ log_{0.2}( x^3+5x^2+6x+1) = log_{0.2}(-x^3+2x^2+3x) \\ x^3+5x^2+6x+1= -x^3+2x^2+3x \\ 2x^3+3x^2+3x+1=0 $$
(2x+1)(x²+x+1)=0
2x+1=0 или х²+х+1=0
х=-1/2 D=1-4<0- уравнение не имеет корней
Проверка удовлетворения найденного значения х=-1/2 системе, задающей ОДЗ
$$ \left \{ {{(- \frac{1}{2})^3+5(- \frac{1}{2}) ^2+6(- \frac{1}{2})+1>0} \atop {-(- \frac{1}{2})^3+2(- \frac{1}{2})^2+3(- \frac{1}{2})>0}} \right.\Rightarrow\left \{ {{(- \frac{1}{8})+5(\frac{1}{4})-6( \frac{1}{2})+1>0} \atop { \frac{1}{8}+2\cdot \frac{1}{4}- \frac{3}{2}>0}} \right. $$
оба неравенства неверны. х=-1/2 не является корнем уравнения
Ответ. нет корней
Логарифмические уравнения: \(\begin{cases}4^{x+y} =2^{y-x}\\4^{3\log_{\sqrt2}x}=y^4 -5\end{cases}\)
Решение: Давайте попробуем преобразовывать каждое уравнение системы.
1.$$ 4^{x+y}=2^{y-x}; 2^{2(x+y)}=2^{y-x}; 2x+2y=y-x; y=-3x; $$ уже лучше, теперь попробуем преобразовать второе уравнение системы
2.$$ 4^{3log_ \sqrt{2}}x=2^{6log_ 2^{ \frac{1}{2} }x}=2^{12log_2x}=(2^{log_2x})^{12}=x^{12}; x^{12}=y^4-5; $$
Получаем эквивалентную систему $$ \left \{ {{y=-3x} \atop {x^{12}=y^4-5}} \right. $$. Вопрос в том, что делать дальше - конечно же, подставить из 1 во 2 уравнение. $$ x^{12}=(-3x)^4-5; x^{12}=81x^4-5; x^{12}-81x^4+5=0; $$ вот здесь трудно сказать, что вообще делать, очевидна замена переменной $$ t=x^3; t^3-81t+5=0; $$ Делители свободного члена корнями являться не будут. Можно сказать приближенные корни:
$$ t_1=-9,0307; t_2=0,0617; t_3=8,969; $$Логарифмическое уравнение: a)log_1/2(3x-1)=1 b)log_2(2x-1)+log_2(3x-2)=0
Решение: $$ \\\log_{\frac{1}{2}}(3x-1)=1\\ 3x-1>0\\ 3x>1\\ x>\frac{1}{3}\\\\ \Big(\frac{1}{2}\Big)^1=3x-1\\ \frac{1}{2}=3x-1\\ 3x=\frac{3}{2}\\ x=\frac{1}{2} \\ \\\log_2(2x-1)+\log_2(3x-2)=0\\ 2x-1>0 \wedge 3x-2>0\\ 2x>1 \wedge 3x>2\\ x>\frac{1}{2} \wedge x>\frac{2}{3}\\ x>\frac{2}{3}\\\\ \log_2(2x-1)(3x-2)=0\\ 2^0=6x^2-4x-3x+2\\ 1=6x^2-7x+2\\ 6x^2-7x+1=0\\ 6x^2-6x-x+1=0\\ 6x(x-1)-1(x-1)=0\\ (6x-1)(x-1)=0\\ x=\frac{1}{6} \vee x=1\\\\ \frac{1}{6}ot>\frac{2}{3}\\ \underline{x=1}\\ $$Логарифмическое уравнение \(log _{3} (81^{x} + 3^{2x})=3log_{27}90\)
Решение: $$ log _{3} (81^{x} + 3^{2x})=3log_{27}90 \\ log _{3} (81^{x} + 3^{2x})=log_{3}90 \\ 81^{x} + 3^{2x}=90 \\ 3^{4x} + 3^{2x}=90 \\ 3^{2x}(3^{2x}+1)=90 $$
Введем замену $$ t=3^{2x} \\ t^2+t-90=0 \\ (t-9)(t+10)=0 \\ t=9 $$ или $$ t=-10 $$
Вернемся к замене: т. к. любое число в степени не может быть отрицательным, то ответ -10 отбрасываем
$$ 3^{2x}=9 \\ 2x=2 $$
x=1 - корень ураввнения

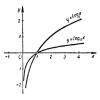 Логарифмической функцией называется функция вида
y = logax,
где а - некоторое фиксированное положительное число, отличное от 1.
Формула y = logax выражает то же самое, что и формула
аy= х. (1)
Отсюда легко установить связь между логарифмической функцией и показательной функцией
у = аx (2)
Если показательная функция (2) описывает изменение степени в зависимости от изменения ее показателя, то ввиду (1) логарифмическая функция, наоборот, описывает изменение...
Логарифмической функцией называется функция вида
y = logax,
где а - некоторое фиксированное положительное число, отличное от 1.
Формула y = logax выражает то же самое, что и формула
аy= х. (1)
Отсюда легко установить связь между логарифмической функцией и показательной функцией
у = аx (2)
Если показательная функция (2) описывает изменение степени в зависимости от изменения ее показателя, то ввиду (1) логарифмическая функция, наоборот, описывает изменение...