логарифм »
логарифмическое уравнение - страница 6
Логарифмические уравнения и неравенства.
Решите уравнения : lg(x-1)+lg(x-2.5) = 1.
Решение: lg(x-1)+lg(x-2.5) = 1. Так как в этом ур-е представлена сумма логарифмов с одинаковым основанием, то сложение заменяется умножением, а логарифм с основанием выносится за скобку. Таким образом, получаем следующее:
lg((x-1)*(x-2.5)) = 1. Теперь, 1 заменяем на lg10. Получаем:
lg((x-1)*(x-2.5)) = lg10. У нас получились логарифмы с одинаковым основанием.
x^2-2.5x-x+2.5=10. Дальше уже несложно решить...логарифмическое уравнение\( \frac{1}{5-\lg x}+\frac{2}{1+\lg x}=1 \)
Решение: $$ \\\frac{1}{5-\lg x}+\frac{2}{1+\lg x}=1\\ 5-\lg xot=0\wedge 1+\lg xot=0\\ \lg xot=5 \wedge \lg xot=-1\\ xot=10^5 \wedge xot =10^{-1}\\ xot=10000 \wedge xot = \frac{1}{10}\\ \frac{1+\lg x}{(5-\lg x)(1+\lg x)}+\frac{2(5-\lg x)}{(5-\lg x)(1+\lg x)}=1\\ \frac{1+\lg x+10-2\lg x}{5+5\lg x-\lg x-\lg^2 x}=1\\ \frac{-\lg x+11}{-\lg^2x+4\lg x+5}=1\\ -\lg x+11=-\lg^2x+4\lg x+5\\ \lg^2 x-5 \lg x+6=0\\ $$t=lg x
t²-5t+6=0
Δ=(-5)²-4*1*6
Δ=25-24
Δ=1
√Δ=1
t₁=(-(-5)-1)/(2*1)
t₁=4/2
t₁=2
t₂=(-(-5)+1)/(2*1)
t₂=6/2
t₂=3
lg x=2
x=10²
x=100
lg x=3
x=10³
x=1000
x=100 ∨ x=1000

Логарифмическое уравнение \(\frac{3}{2}\log_{\frac{1}{4}}(x+2)^2 -3 =\log_{\frac{1}{4}}(4-x)^3 -\log_4(x+6)^3 \)
Решение: У логарифмов выносим степень и у основания логарифмов то же выносим степень получаеться -3log(x+2)-3=-3log(4-x)-3log(6+x) сокращаем на -3
Log(x+2)+1=log(4-x)+log(6+x) переносим в одну сторону и там по свойствам логарифма получаем
Log(x+2)/((4-x)(6+x))=-1 так как у нас оснащаете логарифма 4 то (x+2)/((4-x)(6+x))=1/4 отсюда
4х+8=(4-х)(6+х) и решаем это уравнениеЛогарифмическое уравнение:
\( log_{3} ( x^{2}-6x+17)=2 \)
Решение:Log{3} (x² -6x+17) =2 ;
Log{3} (x² -6x+17) =Log{3} 3² ;
x² -6x+17 = 3² ; * * * x² -6x+17 = 3² >0 * * *
x² -6x+8 = 0 ;
x₁ = 2
x₂ = 4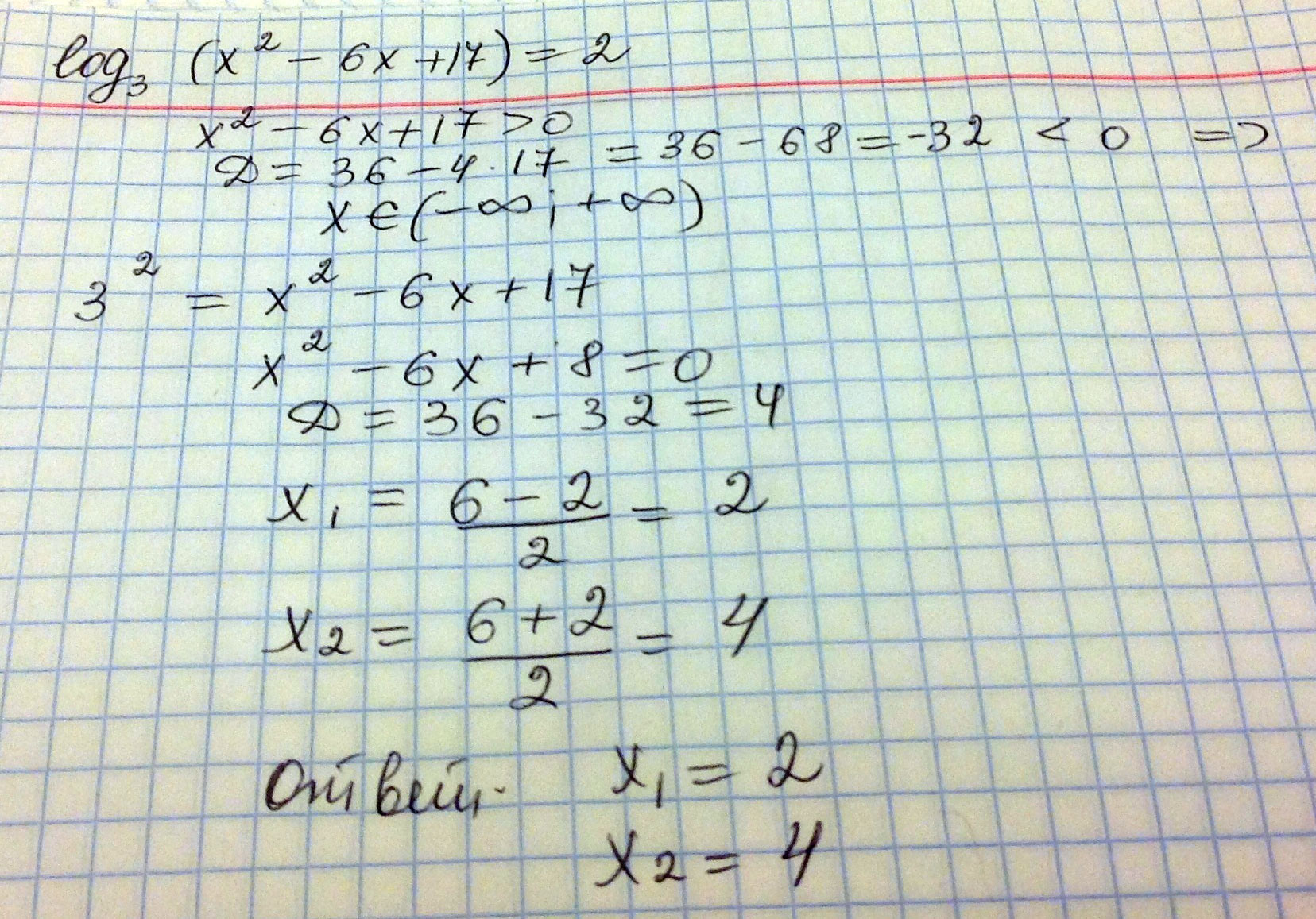
Логарифмическое уравнение:
1) lgx-2lg3=lg7-lg(16-x)
2) \( log_{4}^{2} x+5log_{4} x-6=0 \)
Неравенство:
3) \( log_{2} (x-1) <log_{2} (2x-y) \)
Решение: 1) lg x - 2lg 3 = lg 7 - lg(16-x)
Область определения
{ x>0
{ x<16
x€(0;16)
lg x - lg 9 = lg 7 - lg(16-x)
lg(x/9) = lg(7/(16-x))
x/9 = 7/(16-x)
x(16-x)=7*9
x^2-16x+63=0
(x-7)(x-9)=0
x1=7; x2=9
2) Область определения
x>0
Замена log_4(x)=y
y^2+5y-6=0
(y-6)(y+1)=0
y1=log_4(x)=-1; x1=4^(-1)=1/4
y2=log_4(x)=6; x2=4^6=4096
3) Функция y=log_2(x) возрастающая на всем промежутке области определения.
Поэтому
x-1<2x-y
{ y{ x>1
{ y<2x
Учитывая первые два неравенства, третье будет выполняться всегда, поэтому его можно опустить.
{ x>1
{ y


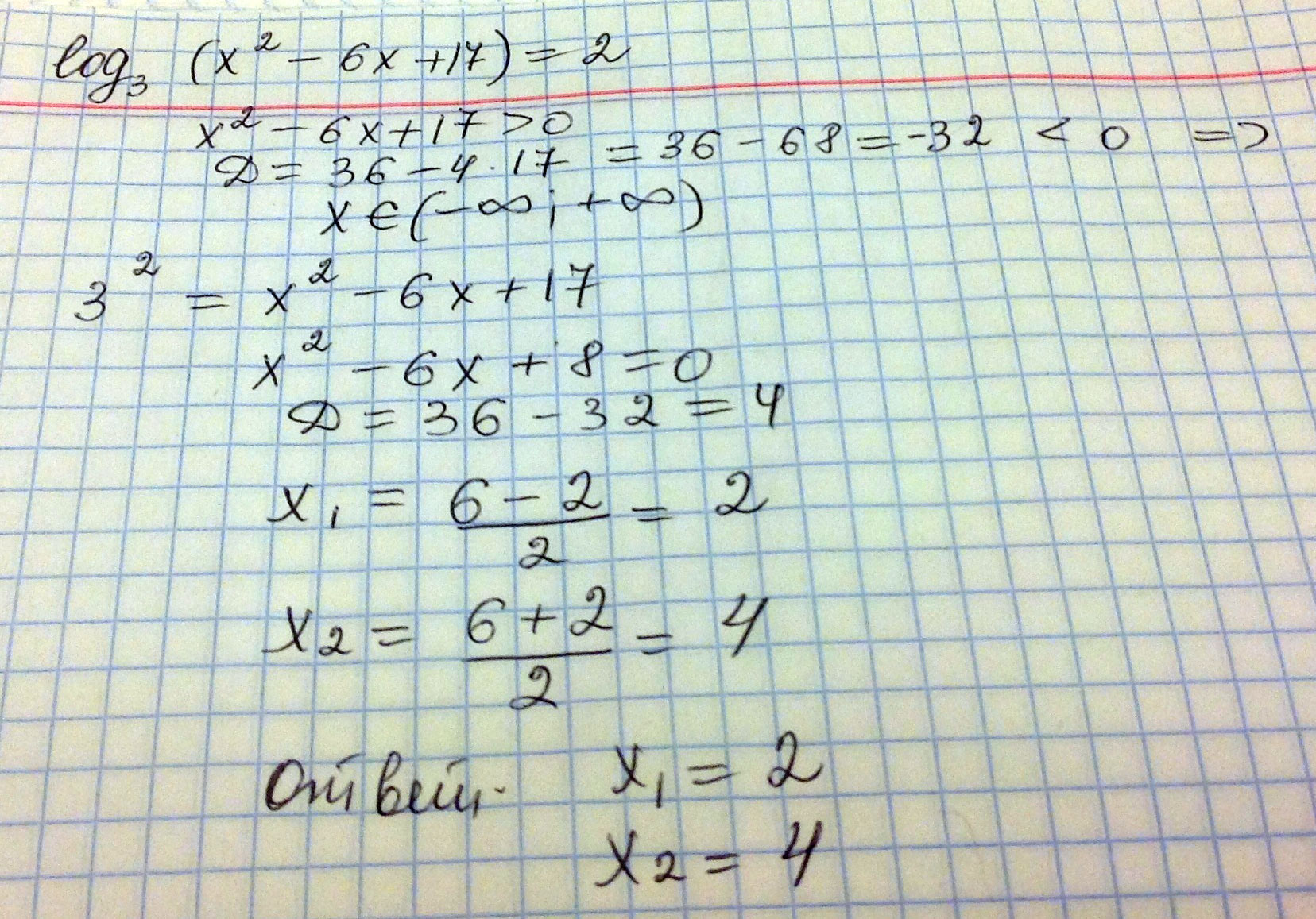
 Логарифмической функцией называется функция вида
y = logax,
где а - некоторое фиксированное положительное число, отличное от 1.
Формула y = logax выражает то же самое, что и формула
аy= х. (1)
Отсюда легко установить связь между логарифмической функцией и показательной функцией
у = аx (2)
Если показательная функция (2) описывает изменение степени в зависимости от изменения ее показателя, то ввиду (1) логарифмическая функция, наоборот, описывает изменение...
Логарифмической функцией называется функция вида
y = logax,
где а - некоторое фиксированное положительное число, отличное от 1.
Формула y = logax выражает то же самое, что и формула
аy= х. (1)
Отсюда легко установить связь между логарифмической функцией и показательной функцией
у = аx (2)
Если показательная функция (2) описывает изменение степени в зависимости от изменения ее показателя, то ввиду (1) логарифмическая функция, наоборот, описывает изменение...