логарифм »
логарифмическое уравнение - страница 4
Решите логарифмические уравнения:
1) \( 3 lg^{2}( x-1) -10lg( x-1) +3=0 \)
2) \( \frac{1}{5-lgx} + \frac{2}{1+lgx} =1 \)
3) \( lg^{2}(100x) + lg^{10x}=14+ lg \frac{1}{x} \)
4) \( lg^{2} x- 2lgx= lg^{2}100-1 \)
Решение: 3*lg²(x-1)-10*lg(x-1)+3=0
lg(x-1)=t ⇒
3t²-10t+3=0 D=64
t₁=3 lg(x-1)=3 x-1=10³ x₁=1001
t₂=1/3 lg(x-1)=1/3 x-1=∛10 x₂=∛10+1
1/(5-lgx)+2/(1+lgx)=1
1+lgx+10-2lgx=-lg²x+4lgx+5
lg²x-5lgx+6=0
lgx=t ⇒
t²-5t+6=0 D=1
t₁=2 lgx=2 x₁=10²=100
t₂=3 lgx=3 x₂=10³=1000
lg²x-2lgx=lg²100-1
lg²x-2lgx=2²-1
lg²x-2lgx-3=0
lgx=t
t²-2t-3=0 D-16
t₁=3 lgx=3 x=1000
t₂=-1 lgx=-1 x=1/10.решить логарифмические уравнения )
lgx-lg11=lg19-lg(30-x)
lgx=2-lg5
Решение: lgx-lg11=lg19-lg(30-x) ОДЗ x>0 ; 30-x > 0 ; x < 30 ; 0 < x <30lg x/11 = lg 19/(3-x)
так как основания логарифмов равны (10)
x/11 = 19/(30-x)
x(30-x) = 19*11
-x^2 +30x -209 =0
x^2 -30x +209 =0
x1 =11 ; x2=19 входят в ОДЗ
lgx=2-lg5 ОДЗ x>0 ;
lgx=lg100-lg5
lgx=lg(100/5) = lg20
так как основания логарифмов равны (10)
x=20 входят в ОДЗ
решить логарифмические уравнения
1) log3(x+5)=2
2) log 1/5(2x+7)=-2
3) log6(x^2+8)=log(6x-1)
4) log3 x+2logx 27-5=0
Решение: 1. log₃(x+5)=2. x+5>0, x>-5
x+5=3², x+5=9
x=4
2. log₁/₅(2x+7)=-2. 2x+7>0, x>-3,5
2x+7=(1/5)⁻²
2x+7=25
x=9
3. log₆(x²+8)=log₆(6x-1)
{x²+8>0
6x-1>0, x>1/6
x²+8=6x-1
x²-6x+9=0, (x-3)²=0
x=3
4. log₃x+2log_x 27 -=0
log₃x+2*(log₃27/log₃x)-5=0
log₃x+6/log₃x-5=0
log₃x=t, t≠0
t²-5t+6=0
t₁=2, t₂=3
1. t₁=2, log₃x=2, x₁=9
2. t₂=3, log₃x=3. x₂=27Тема логарифмические уравнения и неравенства. \(\log_2(x^2+2x-3) \leq \log_2(x+9)\)
Решение: Сначала ОДЗ х² +2х - 3 больше 0
х + 9 больше 0
Первое неравенство имеет решение:(-∞;-3)∨(2;+∞)
второе неравенство имеет решение х больше -9
ОДЗ х∈(-9; -3)∨(2; +∞)
Теперь само решение. Потенцируем. Т. к 2 больше 1, при потенцировании сохраняется знак неравенства
х² + 2х - 3 ≤ х + 9
х² +х -12 ≤ 0
х∈ [ -4; 3]
Учитывая ОДЗ, пишем ответ:
х∈[ -4; -3)∨(2; 3]
Решить уравнения, используя указанные способы: -преобразование и потенцирование в) \(\log_4\log_2x +\log_2\log_4x=2\)
Решите неравенство: а) \(\log_{0,5}\log_6\frac{x^2+x}{x+4}\leq 0\)
б) \(\frac{\log_2(3\cdot 2^{x-1}-1}{x}\geq 0\)
Решите показательное уравнение, используя в решении указанный способ: -разложение на множители: б) \(x^2\cdot 2^{\sqrt{-x}} +4=2^{\sqrt{-x}}+4x^2\); -введение новой переменной: в) \(4^{x-\sqrt{x^2-5}}-12\cdot 2^{x-1-\sqrt{x^2-5}}+8 =0\)
г) \(3^{2x+1}+3^{1-2x}-7(3^x+3^{-x})=4\)
ж) \((\sqrt{5+2\sqrt6})^x +(\sqrt{5-2\sqrt6})^x=10\)
Решение: В) перейдем к основанию 2
(og(2)log(2)x)/2+(log(2)log(2)x)/2=2
2log(2)log(2)x=4
log(2)log(2)x=2
log(2)x=4
x=16
a) ОДЗ
x(x+1)/(x+4)>0
x=0 x=-1 x=-4
_ + _ +
-(-4)-(-1)-(0)-
x∈(-4;-1) U (0;∞)
log(6)[(x²+x)/(x+4)]≥1 (основание меньше 1, знак меняется)
(x²+x)/(x+4)≥6
(x²+x)/(x+4)-6≥0
(x²+x-6x-24)/(x+4)≥0
(x²-5x-24)/(x+4)≥0
x²-5x-24=0
x1+x2=5 U x1*x2=-24⇒x1=-3 U x2=8
x+4=0⇒x=-4
_ + _ +
-(-4)-[-3]-[8]-
x∈(-4;-3] U [8;∞)
б) ОДЗ
1,5*2^x-1>0⇒1,5*2^x>1⇒2^x>2/3⇒x>log(2)(2/3)
{x>0
{log(2)(1,5*2^x-1)≥0⇒1,5*2^x-1≥1⇒1,5*2^x≥2⇒2^x≥4/3⇒x≥log(2)(4/3)
б) ОДЗ x<0
x²*2^√-x+4-2^√-x-4x²=0
2^√-x*(x²-1)-4(x²-1)=0
(x²-1)*(2^√-x-4)=0
x²-1=0
x²=1
x=-1
x=1∉ОДз
2^√-x-4=0
2^√-x=4
√-x=2
-x=4
x=-4
в) ОДЗ x²-5≥0⇒x≤-√5 U x≥√5
4^(x-√(x²-5))-6*2^(x-√(x²-5))+8=0
2^(x-√(x²-5))=a
a²-6a+8=0
a1+a2=6 U a1*a2=8
a1=2⇒2^(x-√(x²-5))=2⇒x-√(x²-5)=1
x-1=√(x²-5)
x²-2x+1=x²-5
-2x=-6
x=3
a2=4⇒2^(x-√(x²-5))=4
x-√(x²-5)=2
x-2=√(x²-5)
x²-4x+4=x²-5
-4x=-9
x=2,25
г)(3^x+3^-x)²=3^2x+3^-2x -2⇒3^2x+3^-2x=(3^x+3^-x)²-2
3(3^x+3^-x)²-6-7(3^x+3^-x)-4=0
3^x+3^-x=a
3a²-7a-10=0
D=49+120=169
a1=(7-13)/6=-1⇒3^x+3^-x=-1 нет решения, т. к. 3^x и 3^-x принимают только положительные значения
a2=(7+13)/6=10/3⇒3^x+3^-x=10/3
3^x=b
b+1/b-10/3=0
3b²-10b+3=0
D=100-36=64
b1=(10-8)/6=1/3⇒3^x=1/3⇒x=-1
b²=(10+8)/6=3⇒3^x=3⇒x=1
ж)(√(5+2√6))^x=a⇒(√(5-2√6))^x=1/a
a+1/a-10=0
a²-10a+1=0
D=100-4=96
√D=4√6
a1=(10-4√6)/2=5-2√6⇒(√(5+2√6))^x=5-2√6⇒x=-1
a2=5+2√6⇒(√(5+2√6))^x=5+2√6⇒x=1
a) ОДЗ x²-3≥0⇒x≤-√3 U x≥√3
9^(√(x²-3)-28/3*3^√(x²-3)+3<0
3^√(x²-3)=a
a²-28a/3+3<0
3a²-28a+9<0
D=784-108=676
a1=(28-26)/6=1/3⇒3^√(x²-3)=1/3⇒√(x²-3)=-1 нет решения
a2=(28+26)/6=9⇒3^(x²-3)=9⇒√(x²-3)=2
x²-3=4
x²=7
x=-√7 U x=√7


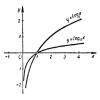 Логарифмической функцией называется функция вида
y = logax,
где а - некоторое фиксированное положительное число, отличное от 1.
Формула y = logax выражает то же самое, что и формула
аy= х. (1)
Отсюда легко установить связь между логарифмической функцией и показательной функцией
у = аx (2)
Если показательная функция (2) описывает изменение степени в зависимости от изменения ее показателя, то ввиду (1) логарифмическая функция, наоборот, описывает изменение...
Логарифмической функцией называется функция вида
y = logax,
где а - некоторое фиксированное положительное число, отличное от 1.
Формула y = logax выражает то же самое, что и формула
аy= х. (1)
Отсюда легко установить связь между логарифмической функцией и показательной функцией
у = аx (2)
Если показательная функция (2) описывает изменение степени в зависимости от изменения ее показателя, то ввиду (1) логарифмическая функция, наоборот, описывает изменение...