логарифм »
логарифмическое уравнение - страница 8
Логарифмическое уравнение\( log _{3} (x-2)+log _{3} (x+6)=2 \)
Решение: $$ log_3(x-2)(x+6)=2 \\ (x-2)(x+6)=3^2 \\ x^2-2x+6x-12=9 \\ x^2+4x-21=0 \\ \left \{ {{x_1+x_2=-4} \atop {x_1*x_2=-21}} \right. \\ x_1=3 \\ x_2=-7 $$
\\\\\\\\\\\\\\\\\\\\\\\\\\

Найдите корень уравнения \(\log_2(6-2x) = 3\log_2 3\)
Решение: $$ log_2(6-2x)=3log_23\; ;\; \; ODZ:\; 6-2x\ > \ 0\; \; \to \; \; x\ < \ 3\\\\log_2(6-2x)=log_23^3\\\\6-2x=27\\\\2x=6-27\\\\x=-10,5\ < \ 3\\\\Otvet:\; x=-10,5 $$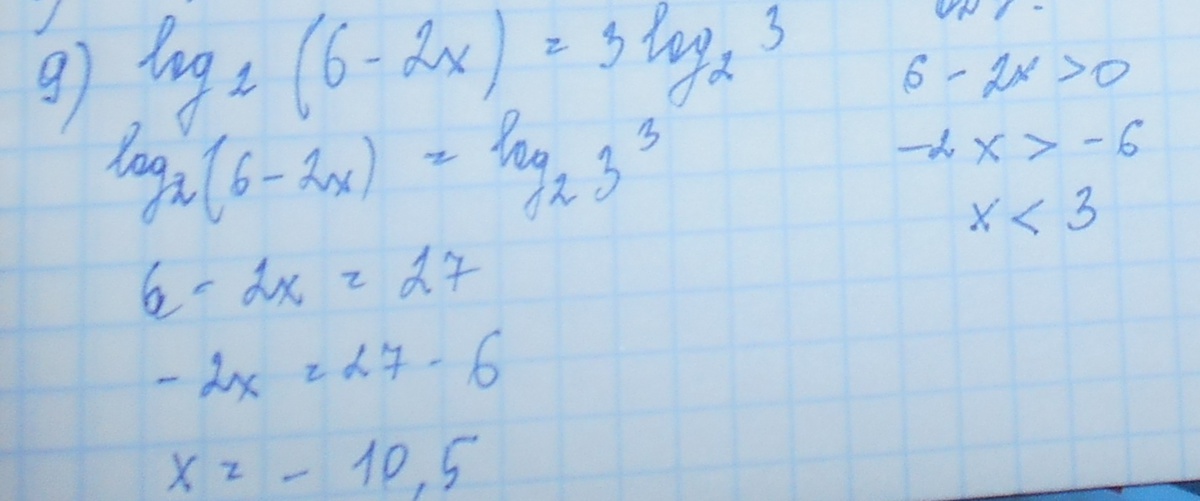
Решите логарифмическое уравнение \(\log_5(x+3)=2-\log_5(2x+1)\)
Решение: X+3>0 U 2x+1>0⇒x>-3 U x>-1/2⇒x>-0,5
log(5)(x+3)+log(5)(2x+1)=2
(x+3)(2x+1)=25
2x²+x+6x+3-25=0
2x²+7x-22=0
D=49+176=225
x1=(-7-15)/4=-5,5 не удов усл
x2=(-7+15)/4=2
ОДЗ:
2x+1>0
x>-0.5
$$ log_5(x+3)+log_5(2x+1)=2\\log_5((x+3)*(2x+1))=2\\2x^2+x+6x+3=5^2\\2x^2+7x-22=0\\D=49+176=225=15^2\\x_1=\frac{-7+15}{4}=2\\x_2=\frac{-7-15}{4}=-\frac{11}{2}=-5.5 $$
x₂ - не входит в ОДЗ.
Ответ: x=2Решите логарифмическое уравнение log0.5(^2+X)=-1
Решение: $$ log_{0,5}(x^2+x)=-1 $$
ОДЗ:
$$ x^2+x>0 \\ x(x+1)>0 \\ x>0 \\ x+1>0 \\ x<-1 $$
x ∈ (-oo;-1) U (0;+oo)
$$ ( \frac{1}{2} )^{-1}=x^2+x \\ \\ 2=x^2+x \\ x^2+x-2=0 \\ D=-b^2-4ac=1^2-4*1*(-2)=1+8=9 \\ \\ x_{1} = \frac{-b+ \sqrt{D} }{2a} = \frac{-1+3}{2} = \frac{2}{2} =1 \\ \\ x_{2} = \frac{-b- \sqrt{D} }{2a} = \frac{-1-3}{2} = \frac{-4}{2} =-2 $$
оба значения удовлетворяют условию x ∈ (-oo;-1) U (0;+oo)
ответ: x1=1, x2= -2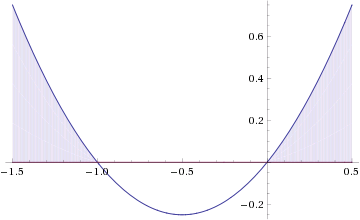
Решите логарифмическое уравнение: \( Log x_{3x} (2.5x+1) ≥ 0\)
Решение: 0 заменить логарифмом 1 по любому основанию. Не понял, какое у вас основание.
А потом воспользоваться свойством возрастания и свойством убывания лог функциии.
Если основание >1, то лог функция возрастает.
Имеем систему двух неравенств.
Первое неравенство, то, что основание больше 1, второе, что выражение под логарифмом больше 1
И вторая система из двух неравенств
0< основание<1, второе выражение под логарифмом больше 1


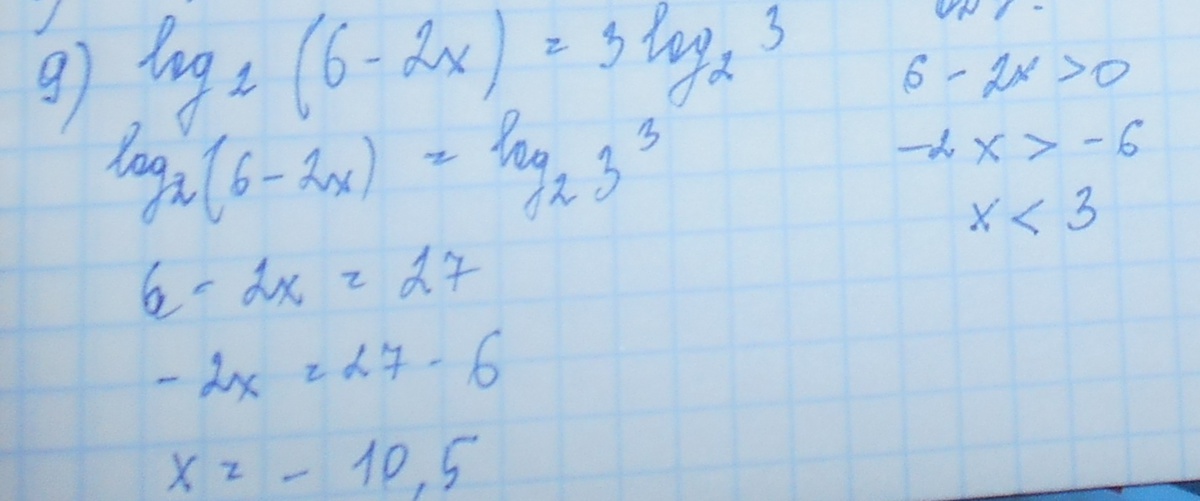

 Логарифмической функцией называется функция вида
y = logax,
где а - некоторое фиксированное положительное число, отличное от 1.
Формула y = logax выражает то же самое, что и формула
аy= х. (1)
Отсюда легко установить связь между логарифмической функцией и показательной функцией
у = аx (2)
Если показательная функция (2) описывает изменение степени в зависимости от изменения ее показателя, то ввиду (1) логарифмическая функция, наоборот, описывает изменение...
Логарифмической функцией называется функция вида
y = logax,
где а - некоторое фиксированное положительное число, отличное от 1.
Формула y = logax выражает то же самое, что и формула
аy= х. (1)
Отсюда легко установить связь между логарифмической функцией и показательной функцией
у = аx (2)
Если показательная функция (2) описывает изменение степени в зависимости от изменения ее показателя, то ввиду (1) логарифмическая функция, наоборот, описывает изменение...