логарифмическое уравнение - страница 9
Решите логарифмическое уравнение:
log2x + log2 (x - 3) = 2
Решение: $$ log_{2}(x(x-3))=log_{2}2^2 $$ ОДЗ:$$ log_{2}(x^2-3x)=log_{2}4 $$ $$ \left \{ {{x>0} \atop {x>3}} \right. \\ x^2-3x=4 \\ x^2-3x-4=0 $$ x>3
$$ D=9+16=25 \\ x_{1}=\frac{3+5}{2}=4 \\ x_{2}=\frac{3-5}{2}=-1 $$ - не удовлетворяет ОДЗ
Ответ: 4

Решите логарифмическое уравнение log3(2x+1)=log3 13+1
Решение: ОДЗ
2x+1>0
2x>-1
x>-0,5
log(3)(2x+1)=log(3)39
2x+1=39
2x=38
x=19
$$ log_3(2x+1)=log_3 13+1 $$
ОДЗ:
$$ 2x+1\ > \ 0 \\ 2x\ > \ -1 \\ x\ > \ -0.5 $$
-(-0.5)-
//////////////////////////
$$ x \in (-0.5;+\infty) \\ log_3(2x+1)=log_3 13+log_33 \\ log_3(2x+1)=log_339 \\ 2x+1=39 \\ 2x=38 \\ x=19 $$
Ответ: 19Логарифмическое уравнение \(x^{\log_4(x)} = 2^{3(\log_4(x)+3)}\)
Решение: Левая часть.
х^log₄x=?
log₄x = logₓ/logₓ4 = 1/logₓ4 = (logₓ4)⁻¹
x^(logₓ4)⁻¹ = (x^logₓ4)⁻¹ = 4⁻¹ = 1/4
правая часть.
2^(3log₄x +9) = 2^3log₄x * 2⁹= (4⁰⁾⁵)^3log₄x * 2⁹ = 4^1,5log₄x * 2⁹ =
=(4^log₄x)¹⁾⁵ * 2⁹ = x¹⁾⁵ *2⁹
само уравнение: 1/4 = х¹⁾⁵ *2⁹,
х¹⁾⁵= 1/4 : 2⁹ = 2⁻¹¹
х¹⁾⁵ = 2⁻¹¹ | ²
x³ = 2⁻²²
x = ∛2⁻²²=1/ ∛2²²= 1/128∛2Решите логарифмическое уравнение log3x-6logx3=1
Решение: Log(b) или log(e,b)- натуральный логарифм числа b
log(10,b) - десятичный логарифм числа b
log(a,b) - логарифм b по основанию alog3x-6*1/log3x=1
(log3x)²-6=log3x
(log3x)²-log3x-6=0
пусть log3x=t t²-t-6=0 t1+t2=1
t1*t2=-6
t1=3 t2=-2
log3x=3 x=3³ x=27
log3x=-2 x=3^-2=1/9
Ответ: х1=27 х2=1/9
Число корней уравнения \(\sqrt{x+2}\cdot \lg(3x^2+5x-11) = 0 \) равно ...?
Решение: Решение
√(x + 2) * lg(3x² + 5x - 11) = 0
1) √(x + 1) = 0, x + 1 = 0
x₁ = - 1
2) lg(3x² + 5x - 11) = 0
3x² + 5x - 11 = 10°
3x² + 5x - 11 - 1 = 0
3x² + 5x - 12 = 0
D = 25 + 4*3*12 = 25 + 144 = 169
x₂ = (- 5 - 13)/6
x₂ = - 3
x₃= (- 5 + 13)/6
x₂ = 8/6
x₃ = 4/3
Проверка:
x₂ = - 3
lg [3(- 3)² + 5(- 3) - 11] = lg (27 - 15 - 11) = lg 1 = 0
верно
x₃ = 4/3
lg [3(4/3)² + 5*(4/3) - 11] = lg (16/3 + 20/3 - 11) = lg(36/3 - 11) =
= lg (12 - 11) = lg 1 = 0
верно
Ответ: Уравнение имеет 3 корня.
x₁ = - 1 ; x₂ = - 3 ; x₃ = 4/3 = 1 (1/3)


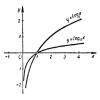 Логарифмической функцией называется функция вида
y = logax,
где а - некоторое фиксированное положительное число, отличное от 1.
Формула y = logax выражает то же самое, что и формула
аy= х. (1)
Отсюда легко установить связь между логарифмической функцией и показательной функцией
у = аx (2)
Если показательная функция (2) описывает изменение степени в зависимости от изменения ее показателя, то ввиду (1) логарифмическая функция, наоборот, описывает изменение...
Логарифмической функцией называется функция вида
y = logax,
где а - некоторое фиксированное положительное число, отличное от 1.
Формула y = logax выражает то же самое, что и формула
аy= х. (1)
Отсюда легко установить связь между логарифмической функцией и показательной функцией
у = аx (2)
Если показательная функция (2) описывает изменение степени в зависимости от изменения ее показателя, то ввиду (1) логарифмическая функция, наоборот, описывает изменение...