логарифм »
логарифмическое уравнение - страница 7
Логарифмическое уравнение \(\log_3^2(9x) +\log_3^2(3x)=1\)
Решение: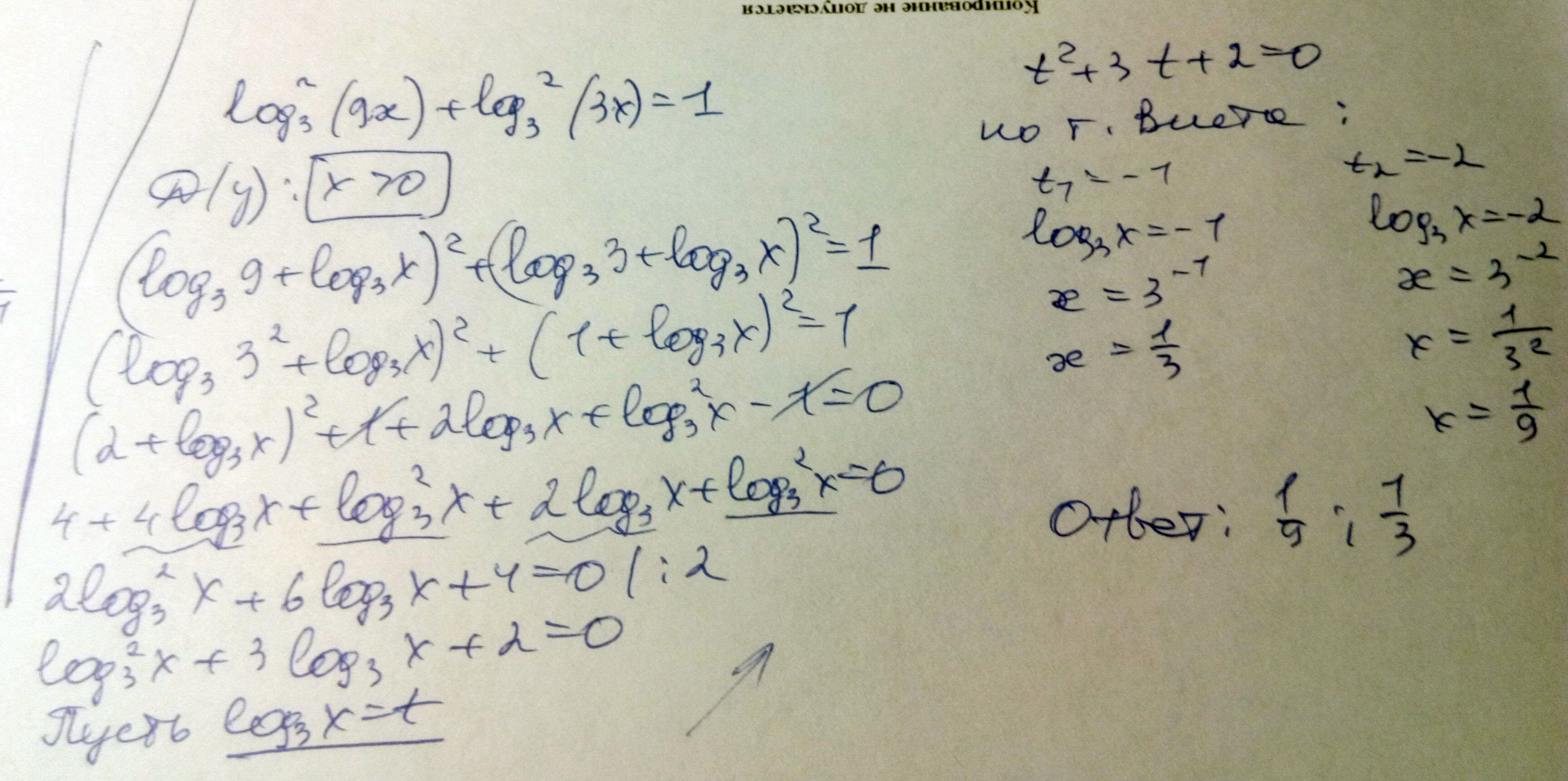
Корень уравнения \(\log_{0,5}(-\frac{1}{\sqrt[3]{-x}})\) принадлежит промежутку ...?
Решение: $$ log_{0,5}( -\frac{1}{\sqrt[3]{-x}} )=\frac{1}{3}\\\\ODZ:\; \; -\frac{1}{\sqrt[3]{-x}}\ > \ 0\;,\; \frac{1}{-\sqrt[3]{x}}\ < \ 0\; \to \; \sqrt[3]{x}\ > \ 0\;,\; x\ > \ 0\\\\log_{\frac{1}{2}}(-\frac{1}{-\sqrt[3]{x}})=\frac{1}{3}\\\\\;,\; \; -log_2(x^{-\frac{1}{3}})=\frac{1}{3}\\\\log_2\, x^\frac{1}{3}=\frac{1}{3}\\\\Po\; opredeleniu:\quad x^{\frac{1}{3}}=2^{\frac{1}{3}} \; \; \to \; \; x=2 \\ 2\in (1;2] $$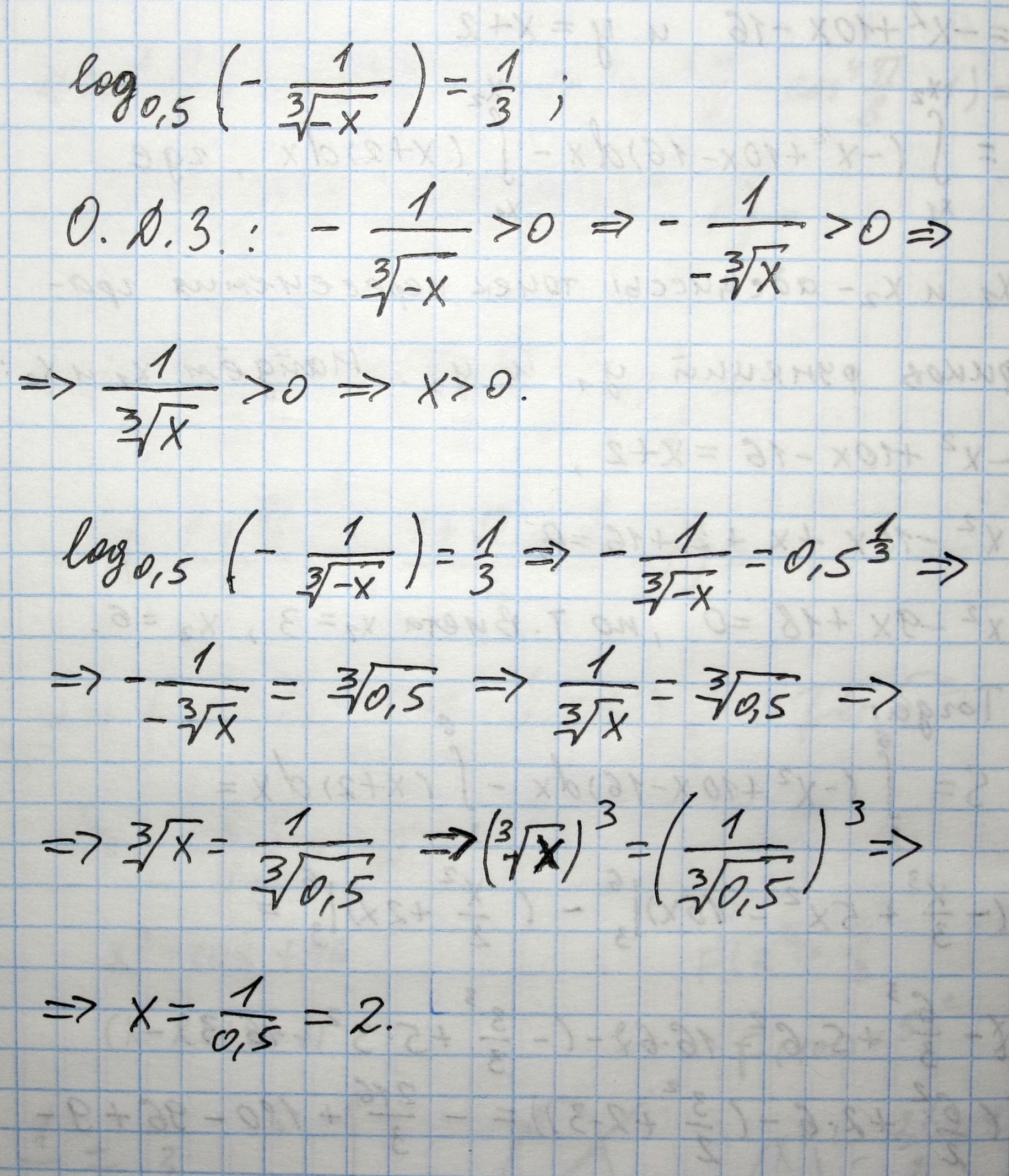
Если \(x_0\) корень уравнения \(\lg8-\lg\sqrt{x+6}=\lg16-\lg(x-2)\), то значение выражения \(x_0^2+x_0+1\) равно ...?
Решение: ОДЗ: √(x+6)>0 x-2>0
x+6>0 x>2
x> -6
В итоге x>2
lg(8/√(x+6))=lg(16/(x-2))
8/√(x+6)=16/(x-2)
8(x-2)=16√(x+6)
x-2=2√(x+6)
(x-2)²=4(x+6)
x²-4x+4=4x+24
x²-4x-4x+4-24=0
x²-8x-20=0
D=64+80=144
x₁=(8-12)/2= -2 - не подходит по ОДЗ.
x₂=(8+12)/2=10
x₀=x₂=10
x₀²+x₀+1=10²+10+1=100+10+1=111
Ответ: б) 111.Логарифмическое уравнение,
\( x^{log _{ \frac{1}{2} } x-3} =4 \)
Решение: $$ x^{ log_{ \frac{1}{2} }x-3 }=4 $$
ОДЗ: $$ x\ > \ 0 \\ log_{ \frac{1}{2} } x^{ log_{ \frac{1}{2} }x-3 }= log_{ \frac{1}{2} } 4 \\ log_{ \frac{1}{2} } x^{ log_{ \frac{1}{2} }x-3 }= log_{ \frac{1}{2} } (\frac{1}{2}) ^{-2} \\ ({ log_{ \frac{1}{2} }x-3 })* log_{ \frac{1}{2} } x={-2} \\ { log_{ \frac{1}{2} }^2x-3log_{ \frac{1}{2} } x+2=0} $$
Замена: $$ log_{ \frac{1}{2} } x=t \\ t^2-3t+2=0 \\ D=(-3)^2-4*1*2=9-8=1 \\ t_1=2 \\ t_2=1 \\ log_{ \frac{1}{2} } x=2 $$ или $$ log_{ \frac{1}{2} } x=1 \\ x= \frac{1}{4} $$ или $$ x= \frac{1}{2} $$
Ответ: $$ \frac{1}{4}\;\;\; \frac{1}{2} $$Логарифмическое уравнение \(\log_4^2x^2+\log_4x^4 = 8\)
Решение: Log²(4)x²+log(4)(x²)²-8=0
log²(4)x²+2log(4)x²-8=0
x≠0
log(4)x²+2a-8=0
a1+a2=-2 U a1*a2=-8
a1=-4⇒log(4)x²=-4⇒x²=1/256⇒x=-1/16 U x=1/16
a2=2⇒log(4)x²=2⇒x²=16⇒x=-4 U x=4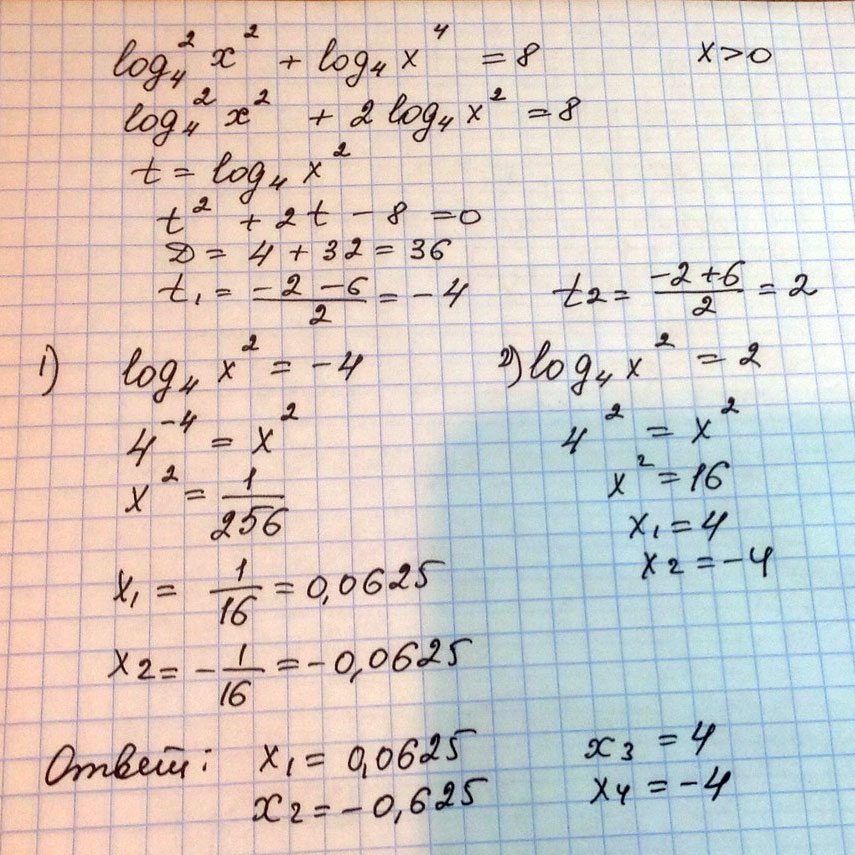

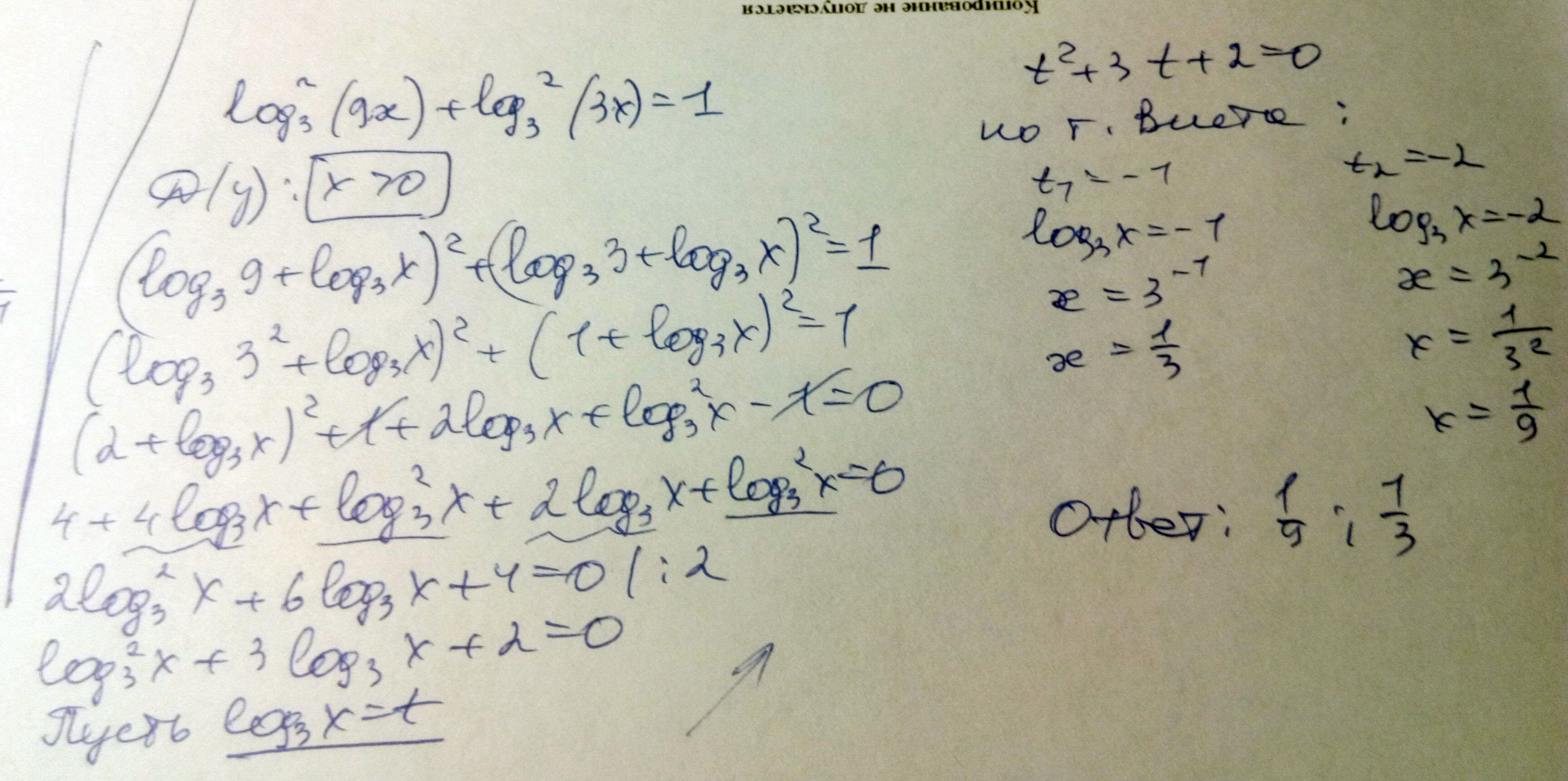
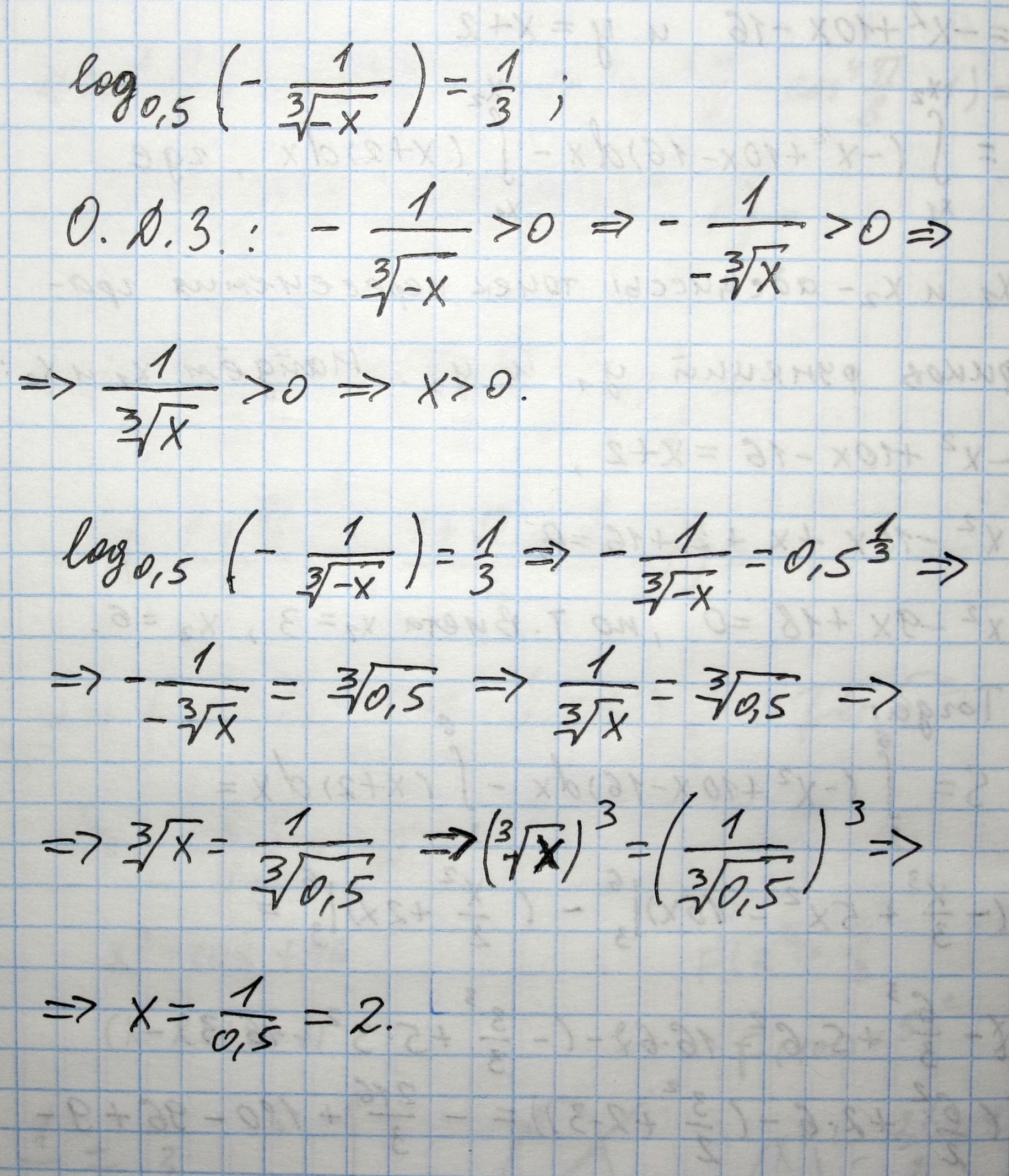
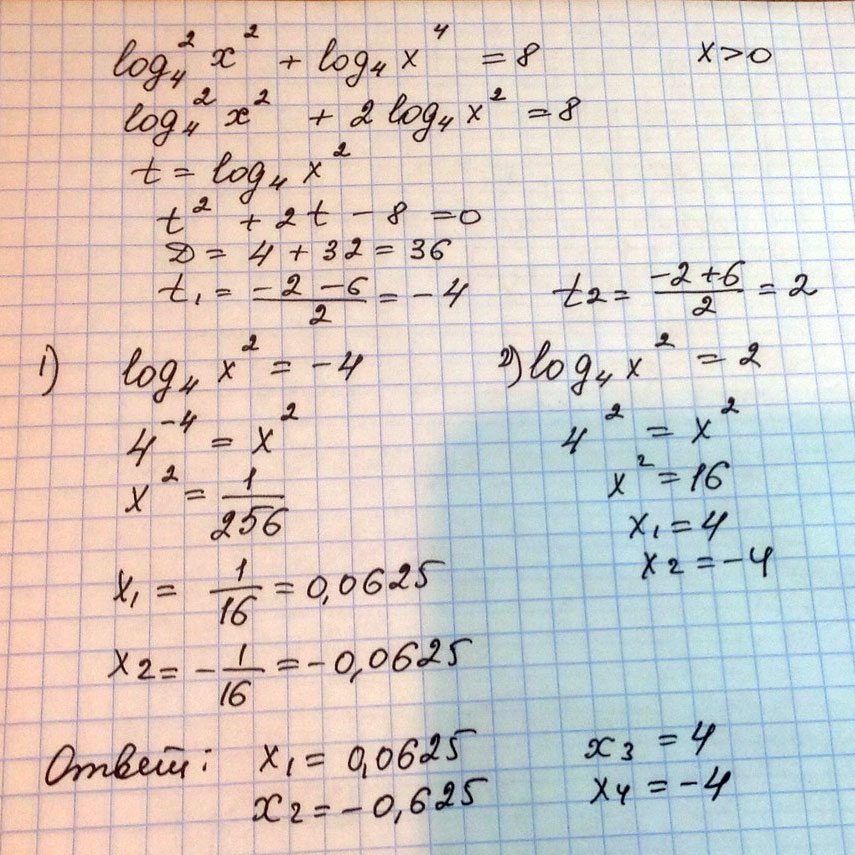
 Логарифмической функцией называется функция вида
y = logax,
где а - некоторое фиксированное положительное число, отличное от 1.
Формула y = logax выражает то же самое, что и формула
аy= х. (1)
Отсюда легко установить связь между логарифмической функцией и показательной функцией
у = аx (2)
Если показательная функция (2) описывает изменение степени в зависимости от изменения ее показателя, то ввиду (1) логарифмическая функция, наоборот, описывает изменение...
Логарифмической функцией называется функция вида
y = logax,
где а - некоторое фиксированное положительное число, отличное от 1.
Формула y = logax выражает то же самое, что и формула
аy= х. (1)
Отсюда легко установить связь между логарифмической функцией и показательной функцией
у = аx (2)
Если показательная функция (2) описывает изменение степени в зависимости от изменения ее показателя, то ввиду (1) логарифмическая функция, наоборот, описывает изменение...